Výška pyramidy: definice, vzorce, výpočty

Jednou z volumetrických postav studovaných v průběhu prostorové geometrie je pyramida. Důležitou vlastností tohoto obrázku je jeho výška. V článku určíme výšku pyramidy a vytvoříme vzorce, kterými je spojena s jinými lineárními charakteristikami.

Co je to pyramida

Pod pyramidou rozumíme geometrický tvar prostoru, který se získá spojením všech rohů polygonu s jedním bodem ve vesmíru. Níže uvedený obrázek ukazuje uspořádání čar (okrajů) pro čtyřhranné a pentagonální pyramidy.

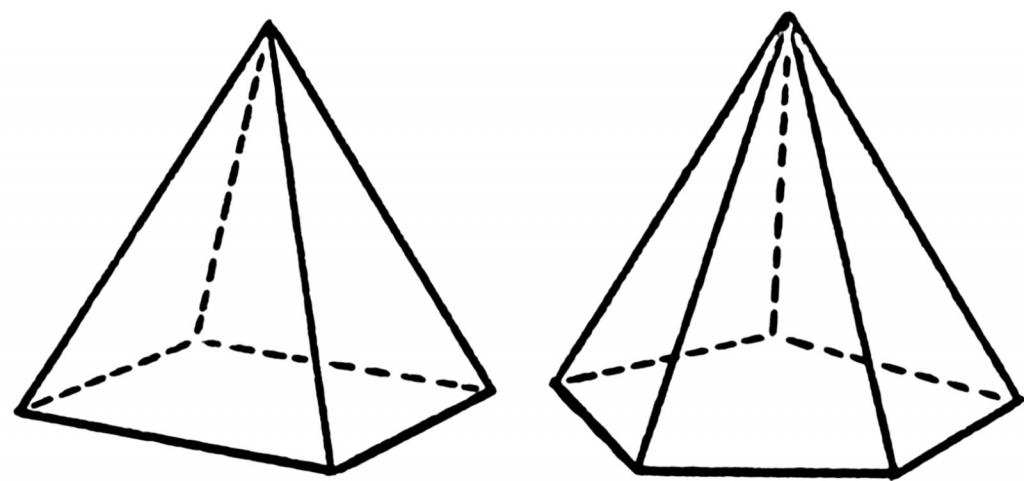
Polygonální tvář tvaru se nazývá její základna. Bod, kde se spojují všechny trojúhelníkové plochy, se nazývá vrchol. Pro určení výšky pyramidy jsou důležité prvky důležité.

Výška těla

Výška pyramidy se nazývá kolmou, která je od horní části spuštěna na rovinu základny. Je důležité si uvědomit, že z každého vrcholu patřícího k základně obrázku je také možné nakreslit kolmici na odpovídající trojúhelníkovou plochu, ale nebude se zdát vysoká. Výška pyramidy je jediná kolmost, která je jednou z jejích důležitých lineárních charakteristik.

Každý školák ví, že každá plochá postava má geometrické centrum (ve fyzice odpovídá středu hmoty). Například geometrický střed libovolného trojúhelníku je určen průsečíkem jeho průměrů, pro rovnoběžník, průsečík diagonálů. Pokud výška pyramidy protíná její základnu v geometrickém středu, pak se tento údaj nazývá přímkou. Pyramida je přímá, má základní polygon se stejnými stranami a úhly, nazvaný správný.

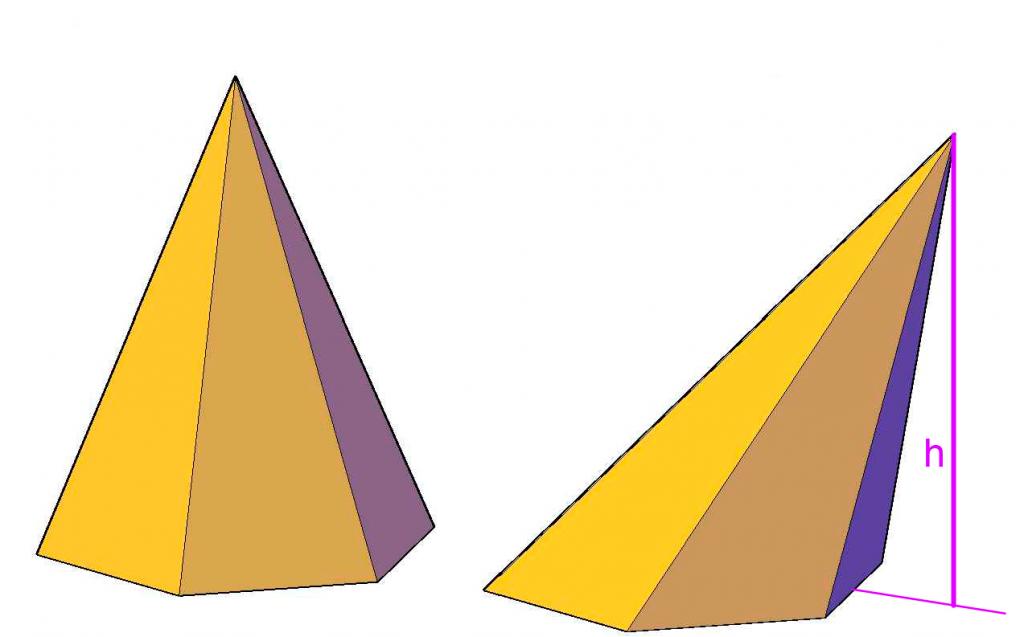
Obrázek nahoře ukazuje rozdíl mezi nesprávnou pyramidou a správnou. Je vidět, že výška nepravidelného tvaru leží nad jeho základnou, zatímco v pravidelné šestiúhelníkové pyramidě je výška uvnitř tvaru a protíná její základnu v geometrickém středu.

Důležité vlastnosti všech pravidelných pyramid jsou následující:

• všechny boční plochy jsou rovnoměrné trojúhelníky a jsou stejné;
• délky bočních žeber a apothem jsou stejné.

Vzory pro výšku pravidelné pyramidy

Existují čtyři základní lineární charakteristiky pro všechny pyramidy správné:

• strana základny;
• boční okraj;
• apothem boční strany;
• výška postavy.

Všechny z nich jsou navzájem matematicky příbuzné. Označte délku strany základny a, výškou - h, apothem - h _b a hranou - b. Formule, které váží tato množství, mají individuální vzhled pro odpovídající n-uhelnou pyramidu. Například pro pravidelnou pyramidu může být čtverhranná výška určena vzorci:

h = √ (a _b ² - a 2/4);

h = √ (b ² - a 2/2).

Tyto vzorce vycházejí z Pythagorovy věty, když se vezmou do úvahy odpovídající pravoúhlé trojúhelníky uvnitř pyramidy.

Pokud se uvažuje o čísle s trojúhelníkovým základem, pak platí následující pravidla pro výšku pravidelné pyramidy:

h = √ (a _b ² - a 2/12);

h = √ (b ² - a 2/3).

Řešení problému s hexagonální pyramidou

Předpokládejme, že dostáváme pravidelnou pyramidu se šestihrannou základnou. Je známo, že výška základny pyramidy je 13 cm. Vědomí, že délka její boční hrany je 10 cm, je nutné vypočítat objem a výšku pravidelné šestiúhelníkové pyramidy.

Níže uvedený obrázek ukazuje, jak vypadá pravidelný šestiúhelník.

Vzdálenost mezi libovolnými jeho dvěma rovnoběžnými stranami se nazývá výška. Není těžké ukázat, že tato výška h _a souvisí s délkou strany obrázku s následujícím vzorem:

h _a = a * 3

Nahrazením hodnoty h _a do výrazu zjistíme, že základní strana a je rovna 7,51 cm.

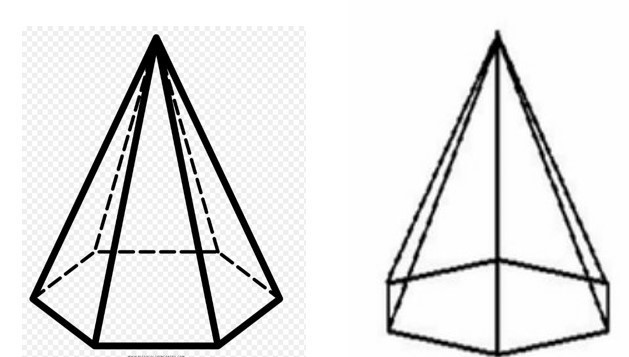
Výšku h čísla lze určit, pokud vezmeme v úvahu pravý trojúhelník uvnitř pyramidy a skládá se ze dvou nohou (výška pyramidy a polovina diagonály šestihranné základny) a hypotenze (boční okraj). Pak se hodnota h rovná:

h = √ (b ² - a ² ) = √ (100 - 56,4) = 6,6 cm.

Objem pyramidy je definován jako třetí část produktu výšky obrázku na ploše jeho základny. Oblast pravidelného šestiúhelníku je:

S ₆ = n / 4 * a ² * ctg (pi / n) = 6/4 * a ² * ctg (pi / 6) = 3 * 4 ≈ 146,53 cm2.

Vzorec použitý pro výpočet S ₆ je univerzální pro libovolný pravidelný n-gon.

K určení objemu obrázku zůstává nahradit parametry nalezené v příslušném vzorci:

V = 1/3 * h * S6 = 1/3 * 6,6 * 146,53 = 322,366 cm3.

Získali jsme hodnotu výšky pyramidy a vypočítali její objem. Problém je tedy vyřešen.