Některé body o tom, jak se vyřeší řešení nerovností
Jedním z témat, která od studentů vyžaduje maximální pozornost a vytrvalost, je řešení nerovností. Ty jsou podobné rovnicím a zároveň se od nich liší. Protože jejich řešení vyžaduje zvláštní přístup.
Vlastnosti, které budou vyžadovány k nalezení odpovědi
Všechny se používají k nahrazení stávajícího záznamu ekvivalentem. Většina z nich je podobná tomu, co bylo v rovnicích. Ale existují rozdíly.
- Funkce definovaná v LDU nebo libovolné číslo může být přidána na obě strany původní nerovnosti.
- Podobně je možné násobení, ale pouze kladnou funkcí nebo číslem.
- Pokud je tato akce provedena s negativní funkcí nebo číslem, musí být znak nerovnosti nahrazen opačným znaménkem.
- Negativní funkce mohou být zvýšeny na pozitivní výkon.
Někdy je řešení nerovností doprovázeno akcemi, které poskytují cizí odpovědi. Musí být vyloučeny porovnáním domény DHS a různými řešeními.
Použití metody rozestupu
Jeho podstatou je snížit nerovnost na rovnici, ve které je na pravé straně nula.
- Určete oblast, kde leží platné hodnoty proměnných, tedy LDL.
- Transformujte nerovnost pomocí matematických operací tak, že v pravé části je nula.
- Nahraďte znaménko nerovnosti "=" a vyřešte odpovídající rovnici.
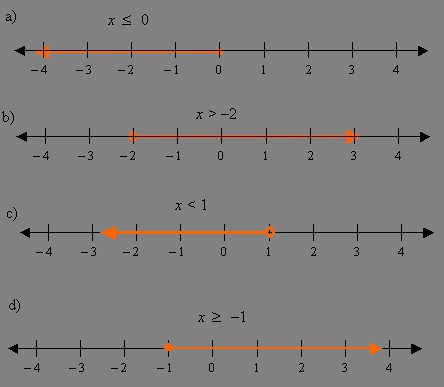
- Na číselné ose označíte všechny odpovědi, které se během řešení objevily, stejně jako intervaly TLD. S přísnou nerovností bodu, který potřebujete nakreslit. Pokud existuje rovnocenné znamení, měly by být převráceny.
- Určete znaménko původní funkce v každém intervalu, které je výsledkem bodů LDD a rozdělíte jeho odpovědi. Pokud při přechodu přes bod se znak funkce nezmění, pak se dostane do odpovědi. Jinak - vyloučeno.
- Hraniční body pro TLD je třeba dodatečně zkontrolovat a teprve pak do odpovědi zahrnout nebo ne.
- Získaná odpověď musí být napsána ve formě sjednocených sad.
Něco o dvojitých nerovnostech
V záznamu používají dva znaky nerovnosti. To znamená, že některé funkce jsou podmínky omezeny okamžitě dvakrát. Takové nerovnosti jsou řešeny jako systém dvou, když je originál rozdělen na části. V intervalové metodě jsou uvedeny odpovědi z řešení obou rovnic.
Pro jejich vyřešení je také možné použít výše uvedené vlastnosti. S jejich pomocí je vhodné snížit nerovnost na nulu rovnosti.

Jaká je situace s nerovnostmi, ve kterých existuje modul?
V tomto případě řešení nerovností používá následující vlastnosti a platí pro pozitivní hodnotu "a".
Pokud "x" má algebraický výraz, pak jsou tyto substituce pravdivé:
- | x | <a až -a <x <a;
- | x | > a na x <-a nebo x> a.
Pokud nejsou nerovnosti přísné, pak jsou vzorce také pravdivé, pouze v nich, s výjimkou znamení více či méně, se objeví "=".
Jak vyřešit systém nerovností?
Tato znalost bude vyžadována v případech, kdy je daný úkol zadán, nebo je zaznamenána dvojnásobná nerovnost nebo se v záznamu objeví modul. V takovém případě by řešení bylo hodnotami proměnných, které by uspokojily všechny nerovnosti v záznamu. Pokud taková čísla neexistují, systém nemá žádné řešení.
Plán řešení tohoto systému nerovností:
- vyřešit každý z nich zvlášť;
- nakreslete všechny mezery na numerické ose a určete jejich průsečíky;
- napište odpověď systému, která bude spojením toho, co se stalo ve druhém odstavci.
Jak se vypořádat s frakčními nerovnostmi?
Vzhledem k tomu, že při jejich řešení může být nutné změnit znamení nerovnosti, je nutné provádět všechny body plánu velmi pečlivě a pečlivě. Jinak to může být opačná odpověď.
Řešení frakčních nerovností také používá intervalovou metodu. Akční plán bude:
- Použitím popsaných vlastností poskytněte zlomek takový vzhled, že vpravo od značky zůstane pouze nula.
- Nahraďte nerovnost "=" a určete body, ve kterých bude funkce roven nule.
- Označte je na ose souřadnic. V tomto případě budou čísla vyplývající z výpočtů v jmenovateli vždy propíchnuta. Všechny ostatní - založené na podmínkách nerovnosti.
- Určete intervaly konzistence.
- V odpovědi napište spojení těchto intervalů, jehož znamení odpovídá tomu, co bylo v původní nerovnosti.
Situace, kdy se nerovnost projevuje iracionality
Jinými slovy, v záznamu je matematický kořen. Vzhledem k tomu, že ve školním kurzu algebry jde většina úkolů druhá odmocnina pak to bude zváženo.
Řešením iracionálních nerovností je získat systém dvou nebo tří, který bude rovnocenný původnímu.
| Původní nerovnost | podmínky | ekvivalentní systém |
| √ n (x) <m (x) | m (x) je menší nebo rovno 0 | žádná řešení |
| m (x) větší než 0 | n (x) je větší nebo rovno 0 n (x) <(m (x)) 2 | |
| √ n (x)> m (x) | m (x) je větší nebo rovno 0 n (x)> (m (x)) 2 | |
nebo n (x) je větší nebo rovno 0 m (x) je menší než 0 | ||
| √n (x) ≤ m (x) | m (x) je menší než 0 | žádná řešení |
| m (x) je větší nebo rovno 0 | n (x) je větší nebo rovno 0 n (x) ≤ (m (x)) 2 | |
| √n (x) ≥ m (x) | m (x) je větší nebo rovno 0 n (x) ≥ (m (x)) 2 | |
nebo n (x) je větší nebo rovno 0 m (x) je menší než 0 | ||
| √ n (x) <√ m (x) | n (x) je větší nebo rovno 0 n (x) je menší než m (x) | |
| √n (x) * m (x) <0 | n (x) je větší než 0 m (x) je menší než 0 | |
| √n (x) * m (x)> 0 | n (x) je větší než 0 m (x) větší než 0 | |
| √n (x) * m (x) ≤ 0 | n (x) je větší než 0 m (x) ≤0 | |
nebo n (x) je 0 m (x) - libovolné | ||
| √n (x) * m (x) ≥ 0 | n (x) je větší než 0 m (x) ≥0 | |
nebo n (x) je 0 m (x) - libovolné |
Příklady řešení různých typů nerovností
Abychom dosáhli přehlednosti teorie řešení nerovností, uvádíme níže příklady.
První příklad. 2x - 4> 1 + x
Řešení: pro určení TLD stačí jen pečlivě se podívat na nerovnost. Je tvořen z lineárních funkcí, proto je definován pro všechny hodnoty proměnné.
Teď z obou stran nerovnosti je třeba odečíst (1 + x). Ukázalo se: 2x - 4 - (1 + x)> 0. Po otevření hranatých závorek a jejich zadání platí nerovnost následující forma: x - 5> 0.
Vyrovnáváním to na nulu je snadné najít jeho řešení: x = 5.
Nyní s tímto číslem 5 musíte označit na souřadnicovém paprsku. Poté zkontrolujte znaménka původní funkce. V prvním intervalu od minus nekonečno do 5 můžete zařadit číslo 0 a nahradit ho nerovností, která vznikla transformací. Po výpočtech se ukáže -7> 0. pod obloukem intervalu je třeba podepsat znaménko mínus.
V dalším intervalu od 5 do nekonečna můžete zvolit číslo 6. Poté se ukáže, že 1> 0. Pod obloukem je podepsán znak "+". Tento druhý interval bude odpovědí na nerovnost.
Odpověď: x leží v intervalu (5; ∞).
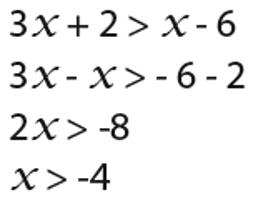
Druhý příklad. Je třeba vyřešit systém dvou rovnic: 3x + 3 ≤ 2x + 1 a 3x - 2 ≤ 4x + 2.
Rozhodnutí. LDL těchto nerovností spočívá také v oblasti libovolných čísel, jelikož jsou uvedeny lineární funkce.
Pak musíte jednat po etapách. Nejprve převeďte první z nerovností a rovno ji na nulu. 3x + 3 - 2x - 1 = 0. To znamená, že x + 2 = 0. Tedy x je -2.
Druhá nerovnost bude mít formu takové rovnice: 3x - 2 - 4x - 2 = 0. Po transformaci: -x - 4 = 0. Hodnota proměnné je -4.
Tato dvě čísla by měla být označena na ose a zobrazovat intervaly. Vzhledem k tomu, že nerovnost není přísná, musí být všechny body namalovány. První interval od mínus nekonečno do -4. Nechť číslo je -5. První nerovnost dá hodnotu -3 a druhá nerovnost, což znamená, že tato mezera není zahrnuta v odpovědi.
Druhý interval je od -4 do -2. Můžete si vybrat číslo -3 a nahradit ho v obou nerovnostech. V první a druhé se získá hodnota -1. Takže pod obloukem "-".
V posledním intervalu od -2 do nekonečna je nejlépe číslo nulové. Je nutné ji nahradit a najít hodnoty nerovností. V prvním z nich se získá kladné číslo a druhé je nulové. Tato mezera by měla být z odpovědi vyloučena.
Ze tří odstupů je řešení nerovnosti pouze jedno.
Odpověď: x patří k [-4; -2].

Třetím příkladem. | 1 - x | > 2 | x - 1 |.
Rozhodnutí. Prvním krokem je určit body, ve kterých funkce zmizí. Vlevo toto číslo bude 2, pro správné číslo 1. Měli by být označeny na paprsku a určeny intervaly znamení stálosti.
V prvním intervalu, od mínus nekonečno k 1, funkce z levé strany nerovnosti přebírá kladné hodnoty a z pravé strany přijímá záporné hodnoty. Pod obloukem musíte zapsat dva znaky "+" a "-" vedle sebe.
Další interval je od 1 do 2. U obou funkcí mají pozitivní hodnoty. Takže, pod obloukem, dva plus.
Třetí interval od 2 do nekonečna dává následující výsledek: levá funkce je záporná, pravá je pozitivní.
Vzhledem k výsledným značkám je nutné vypočítat hodnoty nerovnosti pro všechny intervaly.
Na prvním místě dostaneme následující nerovnost: 2 - x> - 2 (x - 1). Mínus před dvěma v druhé nerovnosti je způsoben skutečností, že tato funkce je negativní.
Po transformaci nerovnost vypadá takto: x> 0. Okamžitě udává hodnoty proměnné. To znamená, že z tohoto intervalu se vrátí pouze interval od 0 do 1.
Na druhé: 2 - x> 2 (x - 1). Konverze poskytnou následující nerovnosti: -3x + 4 více než nula. Jeho nula je x = 4/3. Vzhledem k označení nerovnosti se ukazuje, že x musí být menší než toto číslo. Proto je tento interval snižován na interval od 1 do 4/3.
Druhý uvádí následující nerovnost: - (2 - x)> 2 (x - 1). Jeho transformace vede k následujícímu: x> 0. To znamená, že rovnice platí pro x menší než nula. To znamená, že v požadované mezery nerovnost nedává řešení.
V prvních dvou intervalech se tato hranice ukázala jako číslo 1. Je třeba ji zkontrolovat odděleně. To je, nahradit původní nerovnost. Ukazuje se: | 2 - 1 | > 2 | 1 - 1 |. Výpočet udává, že 1 je větší než 0. Toto je platné prohlášení, takže je součástí odpovědi.
Odpověď: x leží v intervalu (0; 4/3).