Zvláštní teorie relativity. Einsteinova zvláštní a obecná relativita

Poté, co matematici vytvořili pravidla v prostoru pojmů a čísel, vědci byli přesvědčeni, že vše, co museli udělat, bylo experimentovat a vysvětlovat strukturu všech věcí pomocí logických konstrukcí. V rozumných mezích pracují zákony matematiky. Ale experimenty, které přesahují denní koncepce a koncepce, vyžadují nové principy a zákony.

Idea

V polovině devatenáctého století se rozšířila všudypřítomná myšlenka univerzálního vysílání rozšířeného většinou vědců a vědců. Tajemný éter se stal nejčastějším modelem vysvětlujícím fyzické procesy známé v té době. Ale k matematickému popisu éterické hypotézy bylo postupně přidáno množství nevysvětlitelných skutečností, které byly vysvětleny různými dodatečnými podmínkami a předpoklady. Postupně, harmonické teorie éteru zarostlé "berly", se staly příliš mnoho. Nové myšlenky byly potřebné k vysvětlení struktury našeho světa. Postuláty zvláštní teorie relativity splnily všechny požadavky - byly stručné, konzistentní a plně potvrzené experimenty.

Michelsonovy experimenty

Poslední slámou, která roztrhla zadní část éterické hypotézy, byl výzkum v oblasti elektrodynamiky a Maxwellovy rovnice, které je vysvětlovaly. Při uvedení výsledků experimentů do matematického řešení Maxwell použil teorii éteru.

Ve svém experimentu vědci přinutili dva paprsky, které směřovaly různými směry, aby vyzařovaly synchronně. Pokud se světlo pohybuje v "éteru", měl by se jeden paprsek světla pohybovat pomaleji než druhý. Navzdory četným opakováním zkušeností byl výsledek stejný - světlo se pohybovalo konstantní rychlostí.

Jinak nebylo možné vysvětlit skutečnost, že podle výpočtů byla rychlost světla v hypotetickém éteru "vždy stejná, bez ohledu na rychlost, s jakou se pozorovatel pohyboval. Abychom však mohli vysvětlit výsledky výzkumu, bylo nutné, aby referenční rámec byl "ideální". To odporovalo Galileoově postulátu o invarianci všech inerciálních referenčních systémů.

Nová teorie

Na počátku dvacátého století celá galaxie vědců začala rozvíjet teorii, která by sladila výsledky studia elektromagnetických kmitů se zásadami klasické mechaniky.

Při vývoji nové teorie bylo zohledněno, že:

- pohyb s téměř rychlostí světla mění vzorec druhého zákona Newtona, který se týká zrychlení silou a hmotností;

- rovnice pro tělový impuls musí mít jiný, složitější vzorec;

- rychlost osvětlení zůstal konstantní, bez ohledu na zvolený referenční systém.

Úsilí A. Poincaré, G. Lorenze a A. Einsteina vedlo k vytvoření speciální teorie relativity, která se shodla na všech nedostatcích a vysvětlila stávající pozorování.

Základní pojmy

Základem speciální teorie relativity jsou definice, s nimiž tato teorie funguje.

1. Referenční systém je materiálové těleso, které lze považovat za začátek referenčního systému a časovou souřadnici, během které pozorovatel bude sledovat pohyb objektů.

2. Inerciální referenční systém je ten, který se pohybuje rovnoměrně a přímočaře.

3. Událost. Speciální a obecná teorie relativity považujte událost za prostorově lokalizovaný fyzický proces s omezenou dobou trvání. Souřadnice objektu lze specifikovat v trojrozměrný prostor as (x, y, z) a časové období t. Standardním příkladem takového procesu je záblesk světla.

Zvláštní teorie relativity považuje inerciální referenční systémy, u kterých se první systém pohybuje v blízkosti druhé s konstantní rychlostí. V tomto případě je hledání vztahů souřadnic objektu v těchto inerciálních systémech prioritou SRT a je součástí jeho hlavních úkolů. Zvláštní teorie relativity dokázala tuto otázku řešit pomocí Lorentzových vzorců.

STO postuluje

Při vývoji teorie Einstein odmítl všechny četné předpoklady, které byly nezbytné pro podporu teorie éteru. Jednoduchost a matematická prokazatelnost jsou dvě velryby, na nichž spočívala jeho zvláštní teorie relativity. Stručně, jeho předpoklady lze snížit na dva postuláty, které byly potřebné k vytvoření nových zákonů:

1. Všechny fyzické zákony v inerciálních systémech jsou prováděny stejným způsobem.
2. Rychlost světla ve vakuu je konstantní, nezávisí na poloze pozorovatele a jeho rychlosti.

Tyto postuláty zvláštní teorie relativity učinily teorii o mythickém éteru neužitečnými. Namísto této látky byla navržena koncepce čtyřrozměrného prostoru spojující čas a prostor společně. Při určování polohy těla v prostoru je třeba vzít v úvahu čtvrtou souřadnici - čas. Tato myšlenka je poněkud umělá, ale je třeba poznamenat, že potvrzení tohoto pohledu spočívá v rychlostech odpovídajících rychlosti světla a v běžném světě zákony klasické fyziky dělají svou práci dokonale. Galilejský princip relativity je splněna pro všechny inerciální referenční rámce: pokud je pravidlo F = ma pozorováno v CO k, pak bude správné v jiném referenčním rámci k '. V klasické fyzice je čas určitým množstvím a jeho hodnota je neměnná a nezávisí na pohybu inerciálního FR.

Převedení na čerpací stanici

Stručně, souřadnice bodu a času mohou být označeny jako:

x '= x - vt a t' = t.

Tento vzorec dává klasickou fyziku. Zvláštní teorie relativity nabízí tento vzorec ve složitější podobě.

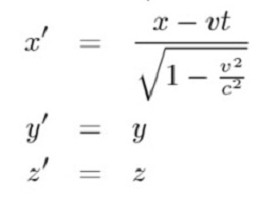
V této rovnici jsou veličiny (x, x 'y, y' z, z 't, t') označeny souřadnicemi objektu a průtokem času v pozorovaných referenčních systémech, v je rychlost objektu a c je rychlost světla ve vakuu.

Rychlost objektů v tomto případě musí odpovídat nestandardnímu systému Galilean

vzorec v = s / t a takovou Lorentzovou transformaci:

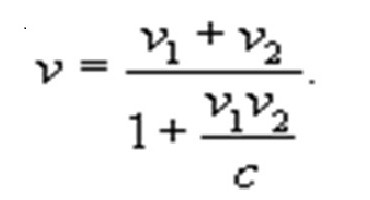
Jak je vidět, při zanedbatelné rychlosti těla se tyto rovnice degenerují v rámci známých rovnic klasické fyziky. Pokud dáváme přednost jinému extrému a nastavíme rychlost objektu, který se rovná rychlosti světla, pak v tomto omezujícím případě je stále dosaženo c. Zvláštní teorie relativity tedy dospívá k závěru, že žádné tělo v pozorovatelném světě se nemůže pohybovat rychlostí převyšující rychlostí světla.

Důsledky SRT

Při další úvaze o Lorentzových transformacích je zřejmé, že s standardními objekty se začínají dělat nestandardní věci. Důsledky zvláštní teorie relativity jsou změna délky objektu a toku času. Pokud se délka segmentu v jednom referenčním rámci rovná l, pak pozorování z jiného operačního systému poskytnou následující hodnotu:

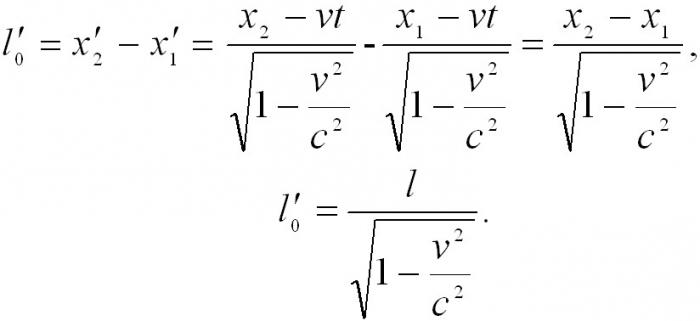
Ukazuje se tedy, že pozorovatel z druhého referenčního systému uvidí segment kratší než první.

Úžasná transformace se dotkla a byla tak veliká jako čas. Rovnice pro souřadnice t bude vypadat takto:

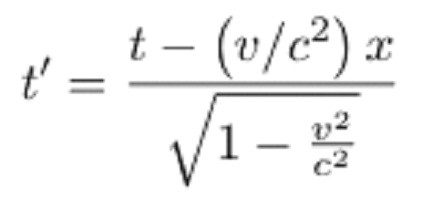
Jak vidíte, čas ve druhém referenčním rámci probíhá pomaleji než v prvním. Samozřejmě, obě tyto rovnice přinesou výsledky pouze při rychlostech srovnatelných s rychlostí světla.

Prvním, který odvodí vzorec časové dilatace, je Einstein. Také nabídl, že vyřeší tzv. "Dvojí paradox". Podle podmínek tohoto úkolu existují dvojčatí bratři, z nichž jeden zůstal na Zemi a druhý z nich vyletěl do vesmíru na raketě. Podle výše uvedeného vzorce budou bratři věk různými způsoby, protože čas pro cestujícího bratra je pomalejší. Tento paradox má řešení, jestliže se domníváme, že bratr-homebody byl vždy v inerciálním referenčním rámci, zatímco dvojčata vycvičovala v non-inertial CO, který se pohyboval s akcelerací.

Změna hmotnosti

Dalším důsledkem SRT je změna hmotnosti pozorovaného objektu v různých CO. Vzhledem k tomu, že všechny fyzikální zákony jsou platné ve všech inerciálních referenčních systémech, musí být dodržovány základní zákony ochrany - hybnost, energie a moment hybnosti. Ale jelikož rychlost pozorovatele v stacionárním CO je větší než rychlost v pohybujícím se, pak podle zákona o zachování hybnosti musí být hmotnost objektu změněna o hodnotu: 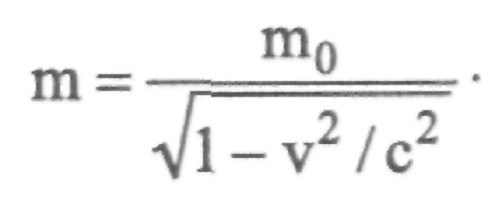V prvním referenčním systému musí mít objekt větší tělesnou hmotnost než ve druhé.

Vzhledem k tomu, že rychlost těla se rovná rychlosti světla, dostáváme neočekávaný závěr - hmotnost objektu dosahuje nekonečné hodnoty. Samozřejmě, každé hmotné tělo obsaženého vesmíru má konečnou hmotnost. Rovnice říká, že žádný fyzický objekt se nemůže pohybovat rychlostí světla.

Poměr hmotnosti a energie

Když je rychlost objektu mnohem nižší než rychlost světla, rovnice pro hmotnost může být redukována na formu:

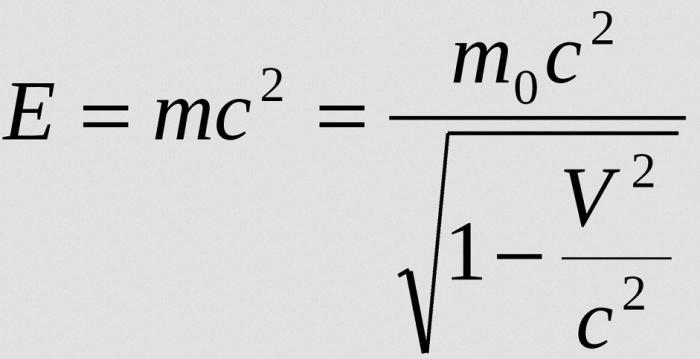
Výraz m 0c je určitá vlastnost objektu, která závisí pouze na jeho hmotě. Tato hodnota se nazývá zbytek energie. Součet energií odpočinku a pohybu lze psát takto:

mc ² = m ₀ c + E _kin .

Z toho vyplývá, že celková energie objektu může být vyjádřena vztahem:

E = mc ² .

Jednoduchost a elegance vzorce tělesné energie poskytla úplnost,

kde E je celková energie těla.

Jednoduchost a elegance slavného vzorce Einsteina poskytla úplnost speciální teorii relativity, která je vnitřně konzistentní a nevyžaduje mnoho předpokladů. Vědci tak vysvětlovali řadu protikladů a podněcovali studium nových fenoménů přírody.