Tělo bylo vrháno pod úhlem k horizontu: rychlost, dosah a výška

V tomto článku budeme analyzovat situaci, kdy tělo bylo hodeno pod úhlem k horizontu. To by mohlo být co by kamenem dohodil s rukou, výstřel z děla, spuštění šípu z luku a tak dále. Všechny uvedené situace jsou popsány stejně z matematického pohledu.

Funkce pohybu v úhlu k horizontu

Jaké jsou podobnosti výše uvedených příkladů z hlediska fyziky? Spočívá v povaze sil působících na tělo. Během volného letu určitého těla působí na něj pouze dvě síly:

• Závažnost.
• Odpor vzduchu

Pokud je tělesná hmotnost dostatečně velká a její tvar je špičatý (projektil, šipka), může být zanedbáván odpor vzduchu.

Pohyb objektu, hozený v úhlu k horizontu těla, je tedy úkol, ve kterém se objevuje pouze síla gravitace. To určuje tvar trajektorie, který je s přesností popsán parabolickou funkcí.

Rovnice pohybu podél parabolické trajektorie. Rychlost

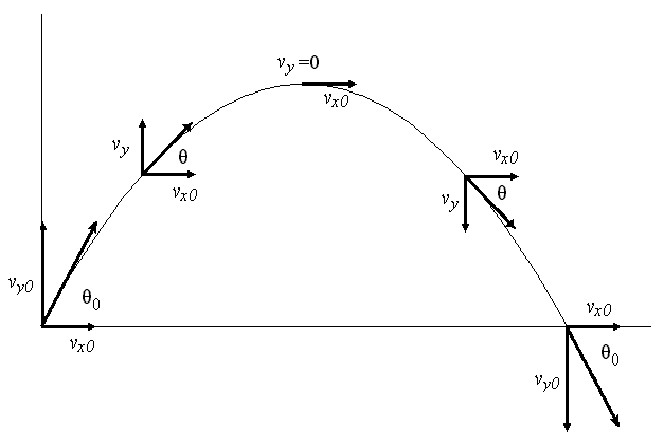
Tělo je vrháno pod úhlem k horizontu. Jak můžete popsat jeho hnutí? Vzhledem k tomu, že jediná síla působící během letu tělesa směřuje dolů, její horizontální složka je nulová. Tento fakt znamená, že vodorovný pohyb objektu je jednoznačně určen počátečními podmínkami (úhel házení nebo výstřel θ a rychlost v). Vertikální pohyb těla je živým příkladem rovnoměrně zrychleného pohybu, kdy konstanta g hraje roli při zrychlení (9,81 m / s ² ).

Vzhledem k výše uvedenému můžeme v době t napsat dvě složky pro rychlost létajícího těla:

v _x = v * cos (θ);

v _y = v * sin (θ) - g * t

Jak je zřejmé, komponenta v _x nezávisí na čase a zůstává konstantní po celou letovou trajektorii (vzhledem k absenci vnějších sil ve směru osy x). Komponenta v _y má maximální hodnotu v počátečním okamžiku. A pak začne klesat, až do té míry, že zmizí v maximálním bodě vzletu těla. Potom se změní jeho znaménko a v době pádu se ukáže, že se rovná modulu počáteční složky v _y , to je v * sin (θ).

Písemné rovnice nám umožňují určit rychlost těla, která se v každém okamžiku hodí do obzoru k horizontu. Jeho modul se bude rovnat:

v = √ (v _x ² + v _y ² ) = √ (v ² * cos ² (θ) + v ² * sin ² (θ) ² ) =

= √ (v ² - 2 * v * sin (θ) * g * t + g ² * t ² )

Rovnice pohybu podél parabolické trajektorie. Rozsah letu

Tělo je vrháno pod úhlem k horizontu. Jakou vzdálenost bude létat? Otázka letového rozsahu se týká změny souřadnic x. Tuto hodnotu lze najít, pokud integrujeme obě složky rychlosti v čase. V důsledku integrace získáváme vzorce:

x = v * cos (θ) * t + x ₀ ;

y = v * sin (θ) * t - g * t 2/2 + y ₀

Rozdíl v souřadnicích x a x ₀ je rozsah. Pokud předpokládáme, že x ₀ = 0, pak bude rozsah rovný x, abychom zjistili, co potřebujete vědět, jak dlouho bude t tělo ve vzduchu.

Druhá rovnice umožňuje vypočítat tuto dobu za předpokladu, že _je známa hodnota y ₀ (výška h, z níž je tělo hodeno). Když objekt dokončí svůj pohyb (padá na zem), jeho souřadnice y se změní na nulu. Vypočítejte čas, kdy k tomu dojde. Máme:

v * sin (θ) * t - g * t 2/2 + h = 0

Před námi je úplná rovnost. Řešíme to prostřednictvím diskriminujícího:

D = v ² * sin ² (θ) - 4 * (-g / 2) * h = v ² * sin ² (θ) + 2 * g * h;

t = (-v * sin (θ) ± √D) / (2 * (-g / 2))

Odmítáme negativní kořen. Získáme následující letový čas:

t = (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)

Nyní nahrazujeme tuto hodnotu za rovnost pro letový rozsah. Máme:

x = v * cos (θ) * (v * sin (θ) + √ (v ² * sin ² (θ)

Pokud je tělo vyhozeno ze země, tedy h = 0, potom bude tento vzorec mnohem jednodušší. A vezměte podobu:

x = 2 * v ² * cos (θ) * sin (θ) / g = v ² * sin (2 * θ)

Poslední výraz byl získán pomocí spojení mezi trigonometrickými funkcemi sinusu a kosinusu (redukční vzorec).

Vzhledem k tomu, že sinus má maximální hodnotu pro pravý úhel, dosáhne se maximálního rozsahu, když je tělo vyhozeno (natočeno) ze země pod úhlem 45 ° a tento rozsah se rovná:

x = v ² / g

Výška těla, hodená pod úhlem k horizontu

Nyní definujeme další důležitý parametr - výšku, ke které může opuštěný objekt vylézt. Je zřejmé, že k tomu je třeba zvážit pouze změnu souřadnic y.

Takže tělo bylo hodené pod úhlem k obzoru, do jaké výšky by to vypadlo? Tato výška bude odpovídat nulové rovnováze složky rychlosti v _y . Máme rovnici:

v _y = v * sin (θ) - g * t = 0

Vyřešte rovnici. Máme:

t = v * sin (θ) / g

Nyní byste měli tento čas nahradit ve výrazu pro souřadnici y. Máme:

y = v * sin (θ) * t - g * t 2/2 + h = v ² * sin ² (θ) / g -

= v ² * sin ² (θ) / (2 x g) + h

Tento vzorec naznačuje, že maximální nadmořská výška, na rozdíl od rozsahu letu, je dosažena tím, že vrhání tělesa je vertikálně (θ = 90). V tomto případě se dostáváme ke vzorci:

y = v ² / (2 x g) + h

Je zajímavé poznamenat, že ve všech vzorcích uvedených v tomto článku se tělesná hmotnost neobjevuje. Charakteristiky parabolické trajektorie jsou nezávislé na tom, ale pouze v nepřítomnosti odporu vzduchu.