Typy algoritmů a příkladů

Programování nahrává něco pomocí cizího cizího jazyka. S rozvojem této oblasti znalostí šli vývojáři ještě dál a naučili se psát něco, aniž by pochopili, jak to zní v ruštině. Začátečníci se naučí psát kód najednou v C ++ nebo php pomocí mnoha knihoven a dokonce ani nepochopí, co vytvářejí zvuky ve svém rodném jazyce. Algoritmizace se zabývá vysvětlením a uvedením tohoto "něčeho".

Algoritmizace

Většina příkladů algoritmů pro výpočetní techniku, dokonce i na univerzitách, je studována na průměrné úrovni. Obvyklou praxí je nekonečné psaní stále složitějšího kódu. Pokusy nezkušených programátorů začít psát programy v programovacím jazyku hned lze porovnat s prací novináře, která sotva zvládla základy cizího jazyka, píše článek pro časopis. Tento problém se můžete vyhnout, pokud začnete nejprve nahrávat svou práci ve svém jazyce, upravovat jej, kontrolovat chyby a na konci překládat do požadovaného jazyka.

Výhodou tohoto přístupu je především to, že developer se bude zabývat překládáním pouze 25% času, při psaní programu v novém jazyce utratí 100% při práci s neznámým jazykem. Současně bude ve stísněných podmínkách a nebude schopen provést dobrou kontrolu chyb a zdokonalení projektu.

Algoritmizace pomáhá při implementaci projektu v počítači popsat proces řešení v nativním a srozumitelném jazyce ve formě diagramu propojených algoritmů, analyzovat myšlenky a získat nejkvalitnější a přemýšlivý kód, který bude odolnější vůči chybám a pracovat efektivněji.

Koncepce algoritmu

Počítač neví, jak řešit problémy, může provádět pouze jednoduché akce v uvedeném pořadí. "Jaká je kalkulačka?" - ptáte se. Je to také ovoce práce programátorů, kteří vytvořili program, který používá určité algoritmy k získání potřebných výsledků. Zvažte abstraktní situaci. Co byste měli udělat, pokud budete vyzváni, abyste našli kořeny čtvercové trinomiální osoby, která není obeznámena s metodami řešení rovnic?

Je zřejmé, že musí být vycvičen. kvadratické rovnice. To se děje takto:

1. Vyberte řešení.
2. Zkontrolujte všechny podrobnosti vybrané metody.
3. Vysvětlete první dva body budoucímu umělci v jazyce, kterému rozumí.

Pak bude možné poskytnout dodavateli úkoly pro řešení kvadratické rovnice. A pokud jsou první dva kroky jednoduché a jasné - všechna řešení jsou popsána v příslušné literatuře, potom je třetí krok obtížný.

Jak se můžete ujistit, že umělci vnímají nápady použité při řešení tohoto problému, jak to chápete? Zde se blížíme pojetí algoritmu. Praxe ukazuje, že k tomu, aby někdo něco správně vysvětlil, je třeba postupovat následovně:

• určuje zdrojová data (proměnná a koeficienty kvadratické rovnice);
• dělí proces rozhodování na jedinečně známé součásti pro umělce (diskriminační vzorce a zjištění kořenů);
• uveďte pořadí kroků (nejprve vypočítat diskriminační, pak kořeny);
• zadejte podmínky, za kterých je řešení považováno za úplné (zkontrolujte nalezené kořeny a nahraďte je do rovnice pro místo proměnných);
• přesně uveďte, jak by měl být výsledek řešení (kořeny patří k souboru reálných čísel).

Popisovaná sada kroků v obecném smyslu je algoritmus. Takto lze algoritmus chápat jako metodu řešení problému, napsanou pomocí určitých pravidel, která umožňuje jednoznačně pochopit provedené akce a jejich pořadí. Níže budou podrobněji diskutovány algoritmy a příklady problémů.

Hlavní vlastnosti algoritmu

Diskrétnost Proces řešení problému vždy sestává ze striktně oddělených akcí, tzv. Kroků, které mají specifický pořadí provedení.

Jistota Každý krok by měl být jasný a jednoznačný, a to jak ve smyslu, tak v klíči akce, která má být přijata.

Výkonnost. Tento algoritmus by měl dát výsledek. V tomto případě může být počet kroků v tisících nebo milionech, ale musí vždy vést k výsledku.

Mass. Jakýkoli algoritmus vyvinutý k vyřešení problému by měl být použitelný pro všechny problémy tohoto typu pro všechny platné vstupní data.

Funkce počítače

Chcete-li správně vytvářet algoritmy pro počítače, je důležité pochopit jejich schopnosti. Zvažte nejprve množství, s nimiž počítač pracuje. Obecně lze je rozdělit na číselné a textové, konstantní a variabilní.

Konstantní čísla jsou všechna čísla: 3.15, 100, 10 ⁵ , jejich zvláštnost je invariance v průběhu celého programu. Proměnné mění svou hodnotu během provádění kódu a jsou zpravidla označeny písmeny: x, y, max, min atd.

Textové proměnné, například číselné, jsou konstantní nebo variabilní. V prvním případě se jedná jen o text: "dobrý", "a" a "atd. Ve druhém je symbol stejný jako numerické proměnné: název, město atd. Rozdíl mezi nimi leží hlavně v přidělené paměti počítače pod uskladněním takové proměnné.

Operace, které je počítač schopen provádět:

1. Čtení dat z vstupních zařízení (klávesnice, myši, soubory).
2. Výpočet hodnot pomocí matematických funkcí: sčítání, odečítání, sin, cos, ln atd. - každý programovací jazyk má vlastní sadu vestavěných funkcí.
3. Výstup dat (na obrazovce, na papíře, v síťovém rozhraní).
4. Přechod mezi etapami programu.
5. Srovnání dvou veličin (více, méně, stejných).

Jedná se o základní operace, které mohou provádět většina programovacích jazyků.

Způsoby popisu algoritmů

Verbální. To je nejjednodušší způsob. Příkladem je recept. Použití jednoduchých matematických vzorců je povoleno.

Grafické. Popis pomocí schémat. Jedná se o speciální způsob zápisu algoritmů pomocí obecně přijatého algoritmického jazyka - čísel a bloků, které mají specifický význam: obdélník je jednoduchá akce, vstup / výstup je šikmý rovnoběžník, kosočtverec je podmínkou atd.

Použití algoritmického jazyka. Podobně jako v grafické podobě je to také speciální způsob, jak napsat algoritmus. Existuje mnoho algoritmických jazyků. Jejich pravidla nejsou přísná, jinak by to byl programovací jazyk. Zvažte příklad algoritmu mezd, v závislosti na délce služby, zaznamenané pomocí algoritmického jazyka.

 алг заработная плата (int ST, real ZP)арг STрез ZPначалоесли ST < 5 то zp = 150иначеесли ST <= 15 то ZP = 180иначе ZP = 180 + (ST - 15)*10конец 

Algoritmický jazyk může být nazváno přísnější formou psaní než verbální. Používá se omezená množina slov a jejich konstrukce, stejně jako odsazení. Nevýhodou slovní podoby a algoritmického jazyka je zhoršující se viditelnost algoritmu se zvyšující se jeho velikostí. Proto lze tyto metody použít pouze k vyjádření významu malých algoritmů.

Druhy algoritmů

Existuje obrovské množství algoritmů určených k řešení různých problémů. Například každá učebnice vyšší matematiky obsahuje stovky algoritmů: systémové řešení lineární rovnice nalezení extrému funkce, výpočet integrálu apod. Nicméně po podrobném přezkoumání jejich struktury se ukázalo, že všechny algoritmy lze rozdělit do několika typů. Zvažte tyto typy algoritmů s příklady.

• lineární (výpočet výsledku přidání nebo násobení, výměna hodnot několika proměnných);
• rozvětvení (určení největšího čísla);
• cyklické (třídění pole, faktoriální výpočet).

Jedná se o základní typy. Je také třeba poznamenat, že v řadě literatury je také zdůrazněn čtvrtý typ - rekurzivní. V schematickém zápisu však nemá speciální označení a je implementováno prostřednictvím základních.

Další podrobnosti o každém algoritmu výpočtu s příklady budou popsány níže.

Principy algoritmizace

1. Identifikujte zdrojová data.
2. Vyberte řešení.
3. Rozdělit zvolenou metodu na kroky založené na schopnostech počítače (programovací jazyk).
4. Spusťte algoritmus ve formě schématu, který definuje jasný pořadí kroků.
5. Zobrazuje výsledky výpočtů.
6. Označte přechod na výstupní obvod.

Algoritmus ladění

Člověk dělá chyby, a to je fakt. Hlavním parametrem každého algoritmu by měla být správnost jeho práce. Ladění je proces identifikace a opravy chyb algoritmu. Chcete-li to provést, proveďte určitou sadu zdrojových dat, nazvanou test. Jsou to zpravidla všechny druhy zdrojových dat. Pokud je například vloženo číslo, měl by být algoritmus zkontrolován pro správný provoz s přihlédnutím k: pozitivním, negativním, celočíselným a reálným číslům, nulovým hodnotám apod.

Hlavním nástrojem pro kontrolu přesnosti algoritmu zůstává lidský mozek. Samozřejmě je povoleno používat jiné počítačové nástroje k automatizaci ověření, avšak jedním nebo druhým způsobem se člověk zabývá přípravou testů a analýzou výsledků. V tomto případě vzniká otázka, proč potřebujeme algoritmus, pokud člověk sám vykoná sám sebe? Poté, že hlavním úkolem algoritmu je vícenásobné řešení určitého typu problémů.

Lineární algoritmy

Lineární algoritmus je ten, ve kterém kroky postupují za sebou. Každý algoritmus, který neobsahuje větve a cykly, je lineární. Zvažte příklad algoritmu, který řeší následující problém: vlk a zajíc sedí ve dvou klecích, musíte je vyměnit.

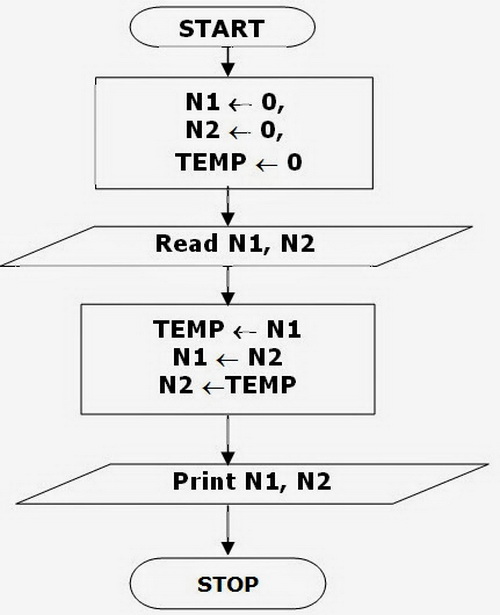
Klíčem k řešení tohoto problému je dodatečná teplota buňky, která by měla být použita k výměně zvířat.

Rozvětvovací algoritmy

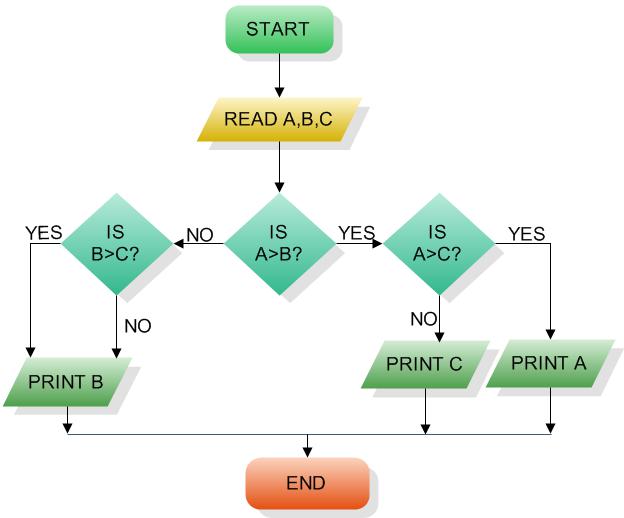
Jak naznačuje název, má algoritmus několik větví. Podstatou práce je výběr jedné z možných variant výpočetního procesu v závislosti na podmínkách. Schématické větvení je reprezentováno blokem ve tvaru kosočtverce, uvnitř kterého je indikován stav, a na jeho stranách jsou vybrané větve v závislosti na tom, zda je podmínka pravdivá nebo nepravdivá. Rozvětvovací algoritmus a příklady jeho aplikace lze nalézt všude. Při programování je to typický konstrukt if-else, který je téměř jakýkoliv jazyk.

Uvádíme příklad algoritmu pro řešení problému nalezení největšího ze tří čísel.

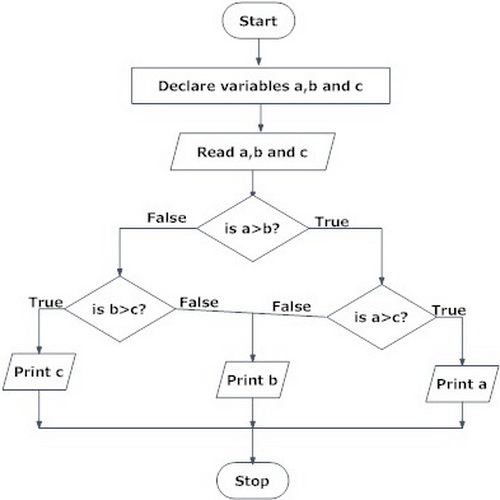
Cyklický algoritmus

Cyklická je algoritmus, ve kterém dochází k opakovaným opakování stejných kroků, ve kterých se může měnit pouze hodnota konkrétní proměnné, nad kterou jsou výpočty provedeny. Druhy cyklických algoritmů a příkladů budou diskutovány níže, ale prozatím budeme seznamovat s hlavními kroky budování cyklu.

1. Přiřazení počáteční hodnoty proměnných. Bez splnění této podmínky nebude cyklus s největší pravděpodobností schopen pracovat nebo chyby.
2. Jednotka vypočte výsledky. Toto je hlavní část cyklu.
3. Zkontrolujte koncové podmínky cyklického procesu. Pokud zapomenete určit podmínku, za jakou má cyklus dokončit, algoritmus bude trvat neomezeně.
4. Změňte proměnné Tento blok se projeví po kontrole stavu ukončení, pokud byl nepravdivý. Pokud zapomeneme na tento blok, cyklus bude vždy provádět jednu akci a nikdy nekončí. Proto je důležité, aby proměnné procházely změnami při každé iteraci smyčky.

Existuje několik typů cyklických algoritmů: s postcondition, předpokladem a parametrem.

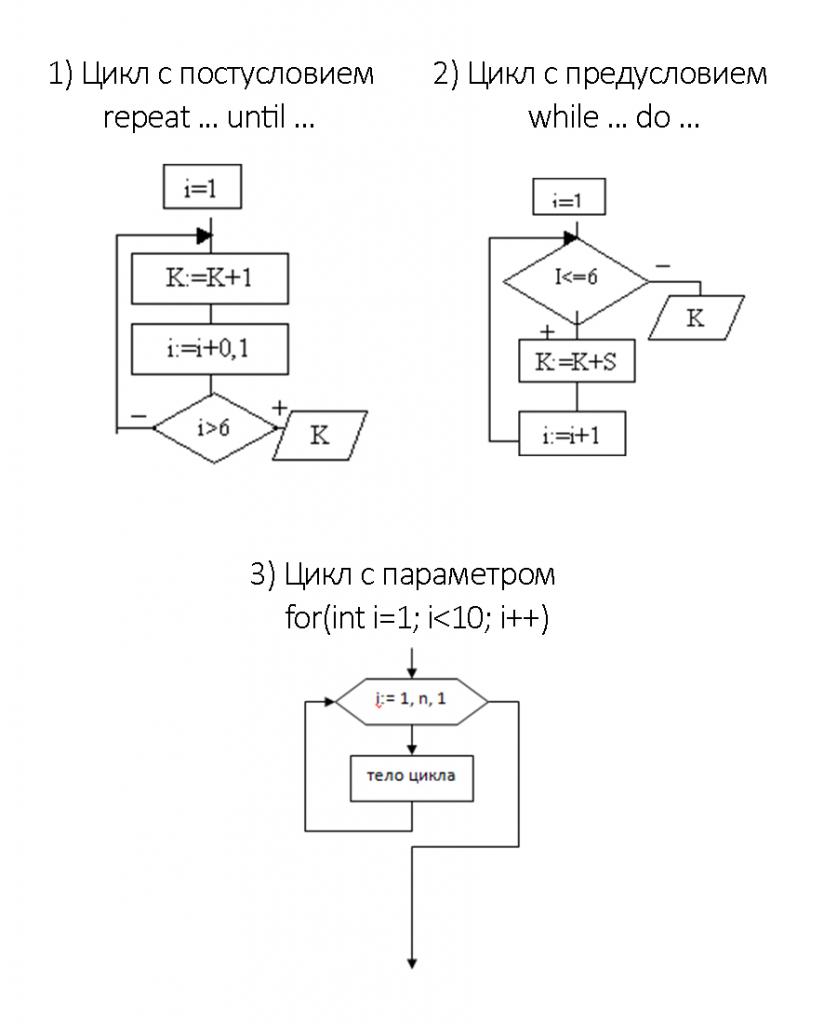
Vytváříme cyklický algoritmus pomocí příkladu nalezení faktoriálu N.

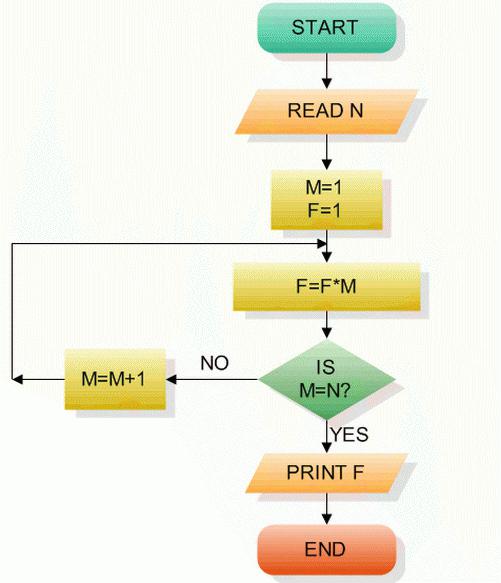
Jiné typy algoritmů

Existuje řada algoritmů, které se liší klasifikací nebo původem.

• Mechanické algoritmy. Například provoz spalovacího motoru nebo montážní linky.
• Pravděpodobnostní algoritmy. Jejich práce vychází z teorie pravděpodobnosti a matematické statistiky.
• Heuristické algoritmy. Použijte praktické úvahy v jejich práci bez přísného matematického zdůvodnění.
• Genetické algoritmy. Aplikujte biologické myšlenky v jejich práci.

A další.