Lineární rovnice: vzorce a příklady. Nerovnosti a jejich řešení
Naučit se řešit rovnice je jednou z hlavních úkolů, které algebra představuje pro studenty. Počínaje nejjednodušším, když se skládá z jednoho neznámého a postupuje se stále více a složitěji. Pokud akce, které je třeba provést s rovnicemi z první skupiny, nejsou pochopeny, bude těžké jednat s ostatními.
Chcete-li pokračovat v konverzaci, musíte se dohodnout na zápisu.
| Název hodnoty | Jeho označení |
| proměnná | x, y |
| libovolné číslo | a, b, c |
Obecný pohled na lineární rovnici s neznámou a princip jejího řešení
Každá rovnice, která může vést k záznamu tohoto typu:
a * x = in ,
lineární . Toto je obecný vzorec. Často jsou však v úlohách implicitně psány lineární rovnice. Potom musíte provést identické transformace, abyste získali obecně uznávaný záznam. Mezi tyto akce patří:
- otevírací konzoly;
- přesunutí všech výrazů s proměnnou na levou stranu rovnice a zbytek doprava;
- takových podmínek.
V případě, kdy je neznámá hodnota v jmenovateli zlomku, je nutné stanovit její hodnoty, u kterých výraz nebude mít smysl. Jinými slovy, je nutné znát doménu rovnice.
Princip, kterým jsou řešeny všechny lineární rovnice, snižuje rozdělení hodnoty na pravé straně rovnosti koeficientem před proměnnou. To znamená, že "x" bude rovno / a.
Zvláštní případy lineární rovnice a jejich řešení
Při odůvodňování mohou takové momenty vznikat, když lineární rovnice mají jeden ze speciálních typů. Každá z nich má specifické řešení.
V první situaci:
a * x = 0 , navíc a ≠ 0.
Řešení takové rovnice bude vždy x = 0.
Ve druhém případě má hodnota "a" hodnotu rovnající se nule:
0 * x = 0 .
Odpověď na tuto rovnici bude libovolné číslo. To znamená, že má nekonečný počet kořenů.
Třetí situace vypadá takto:
0 * x = in , kde v ≠ 0.
Tato rovnice nemá smysl. Protože kořeny, které ho uspokojují, neexistují.

Obecný pohled na lineární rovnici se dvěma proměnnými
Ze svého jména je zřejmé, že v něm jsou již dvě neznámá množství. Lineární rovnice se dvěma proměnnými vypadají takto:
a * x + v * y = s .
Vzhledem k tomu, že v záznamu jsou dvě neznámé, odpověď bude vypadat jako dvojice čísel. To nestačí k zadání pouze jedné hodnoty. To bude neúplná odpověď. Dvojice veličin, u nichž se rovnice změní v identitu, je řešením rovnice. Navíc odpověď je vždy první, která zapíše proměnnou, která se dříve nachází v abecedním pořadí. Někdy říkají, že tato čísla ho uspokojují. Navíc takové páry mohou být nekonečné číslo.
Jak řešit lineární rovnici se dvěma neznámými?
Chcete-li tak učinit, zvedněte libovolný pár čísel, který se ukáže být pravdivý. Pro zjednodušení můžete mít jednu z neznámých, aby se rovnali všem primární číslo a pak najděte druhou.
Při řešení je často nutné provádět akce k zjednodušení rovnice. Jsou nazývány transformace identity. Kromě toho jsou pro rovnice vždy platné následující vlastnosti:
- každý pojem může být převeden na opačnou část rovnosti tím, že nahradí jeho znamení opakem;
- levou a pravou stranu libovolné rovnice lze rozdělit stejným číslem, pokud není rovno nule.

Příklady úkolů s lineárními rovnicemi
První úkol. Řešení lineárních rovnic: 4x = 20, 8 (x - 1) + 2x = 2 (4 - 2x); (5 x 15) / (x + 4) = 4; (5x + 15) / (x + 3) = 4.
V rovnici, která je v tomto seznamu první, stačí jednoduše rozdělit 20 na 4. Výsledek bude 5. Toto je odpověď: x = 5.
Třetí rovnice vyžaduje, aby byla provedena transformace identity. Spočívá v odhalení závorek a přiložení těchto výrazů. Po první akci má rovnice formu: 8x - 8 + 2x = 8 - 4x. Poté je nutné přenést všechny neznámé na levé straně rovnosti a zbytek doprava. Rovnice bude vypadat takto: 8x + 2x + 4x = 8 + 8. Po zmenšení těchto pojmů: 14x = 16. Nyní vypadá stejně jako první a jeho řešení je snadné. Odpověď je x = 8/7. Ale v matematice má být přidělena celá část zlý zlomek. Pak bude výsledek transformován a "x" bude rovno jednomu a jednému sedmému.
Ve zbývajících příkladech jsou proměnné v jmenovateli. To znamená, že nejprve potřebujete vědět, na jakých hodnotách jsou definovány rovnice. K tomu musíte vyloučit čísla, při kterých se jmenovatelé změní na nulu. V prvním příkladu je to "-4", ve druhém je "-3". To znamená, že tyto hodnoty musí být z odpovědi vyloučeny. Poté musíte vynásobit obě strany rovnice výrazy v jmenovateli.
Otevřením konzolí a poskytnutím podobných výrazů získáváme v první z těchto rovnic: 5x + 15 = 4x + 16 a ve druhé 5x + 15 = 4x + 12. Po transformacích je řešení první rovnice x = -1. Druhá se rovná "-3", což znamená, že druhá nemá žádné řešení.
Druhý úkol. Vyřešte rovnici: -7x + 2y = 5.
Předpokládejme, že první neznámý x = 1, pak rovnice má formu -7 * 1 + 2y = 5. Po převedení faktoru "-7" na pravou stranu rovnice a změně jejího znaménka na plus se ukázalo, že 2u = 12. Proto je y = 6. Odpověď: jedno z řešení rovnice je x = 1, y = 6.

Obecný pohled na nerovnost s jednou proměnnou
Zde jsou uvedeny všechny možné situace v oblasti nerovností:
- a * x> v;
- a * x <v;
- a * x ≥ v;
- a * x ≤v.
Obecně platí, že to vypadá jako nejjednodušší lineární rovnice, pouze rovná se znaménko je nahrazeno nerovností.
Stejné transformační pravidla pro nerovnost
Stejně jako lineární rovnice a nerovnosti lze upravit podle určitých zákonů. Vrácejí se na následující:
- může být na levou a pravou stranu nerovnosti přidáno jakékoli doslovné nebo číselné vyjádření, přičemž znaménko nerovnosti zůstává stejné;
- lze také rozmnožit nebo rozdělit stejným kladným číslem, opět se znak nezmění;
- když vynásobíte nebo dělíte stejným záporným číslem, zůstane rovnost za předpokladu, že znak nerovnosti je obrácen.

Obecný pohled na dvojité nerovnosti
Následující problémy nerovností mohou být zastoupeny v problémech:
- v <a * x <s;
- v ≤ a * x <s;
- v <a * x ≤ s;
- v ≤ a * x ≤ c.
Dvojitá je nazývána, protože je omezena známkami nerovnosti na obou stranách. Vyřeší se stejnými pravidly jako běžné nerovnosti. A nalezení odpovědi přichází k řadě shodných transformací. Dokud nebude přijato nejjednodušší.
Vlastnosti řešení dvojí nerovnosti
První z nich je jeho obraz na souřadnicové ose. Tuto metodu není třeba používat pro jednoduché nerovnosti. Ale v obtížných případech to může být prostě nezbytné.
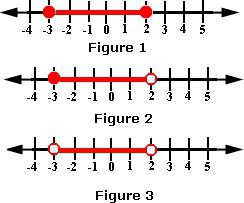
Pro obraz nerovnosti je nutné vyznačit na ose všechny body, které se během odůvodnění objevily. Jedná se o neplatné hodnoty, které jsou označeny punkturovanými body, a hodnoty z nerovností získaných po transformacích. Zde je také důležité správně kreslit body. Pokud je nerovnost přísná, tj. <Nebo>, pak jsou tyto hodnoty propíchnuty. Při slabých nerovnostech musí být body zafarbené.
Poté je třeba označit význam nerovností. To lze provést pomocí šrafování nebo oblouků. Jejich křižovatka bude znamenat odpověď.
Druhá vlastnost souvisí s jeho záznamem. Zde jsou dvě možnosti. První je konečná nerovnost. Druhá je ve formě mezery. Stává se mu, že vzniknou potíže. Intervaly odpovědí vždy vypadají jako proměnná se znaménkem příslušnosti a závorky s čísly. Někdy je několik mezer, pak mezi závorkami je třeba napsat symbol "a". Tyto znaky jsou následující: ∈ a ∩. Rozdílné hrany hrají také roli. Okrouhlý je nastaven, když je bod vyloučen z odpovědi a obdélníková obsahuje tuto hodnotu. Označení nekonečna je vždy v závorkách.
Příklady řešení nerovností
1. Vyřešit nerovnost 7 - 5x ≥ 37.
Po jednoduchých transformacích se ukáže: -5x ≥ 30. Rozdělením "-5" můžete získat následující výraz: x ≤ -6. Toto je odpověď, ale může být napsána jiným způsobem: x ∈ (-∞; -6).
2. Vyřešit dvojitou nerovnost -4 <2x + 6 ≤ 8.
Nejprve je třeba odečíst všude 6. Ukázalo se: -10 <2x ≤ 2. Nyní musíte rozdělit na 2. Nerovnost bude vypadat takto: -5 <x ≤ 1. Po zobrazení odpovědi na číselné ose můžete okamžitě pochopit, že výsledek bude od -5 do 1. A první bod je vyloučen a druhý je zahrnut. To znamená, že odpověď na nerovnost je: x ∈ (-5; 1).