Rovnoměrně zrychlený pohyb. Úkoly a vzorce

Nejdůležitějším znakem pohybu těla je jeho rychlost. Když je známe, stejně jako některé další parametry, můžeme vždy určit čas pohybu, ujetou vzdálenost, počáteční, konečnou rychlost a zrychlení. Rovněž zrychlený pohyb je pouze jeden typ pohybu. Obvykle se vyskytuje ve fyzikálních problémech z kinematiky. Při takových úkolech je tělo přijato materiální bod což výrazně zjednodušuje všechny výpočty.

Rychlost Zrychlení

Nejprve bych chtěl upozornit čtenáře na skutečnost, že tato dvě fyzikální veličiny nejsou skalární, ale vektorová. A to znamená, že při řešení určitého druhu problémů je třeba věnovat pozornost tomu, jaký druh zrychlení má tělo z hlediska znamení, a také co je vektor rychlosti samotného těla. Obecně platí, že ve chvílích výlučně matematického plánu jsou tyto momenty vynechány, ale ve fyzice to je velmi důležité, protože v kinematiku může být odpověď na základě nesprávně daného znamení chybná.

Příklady

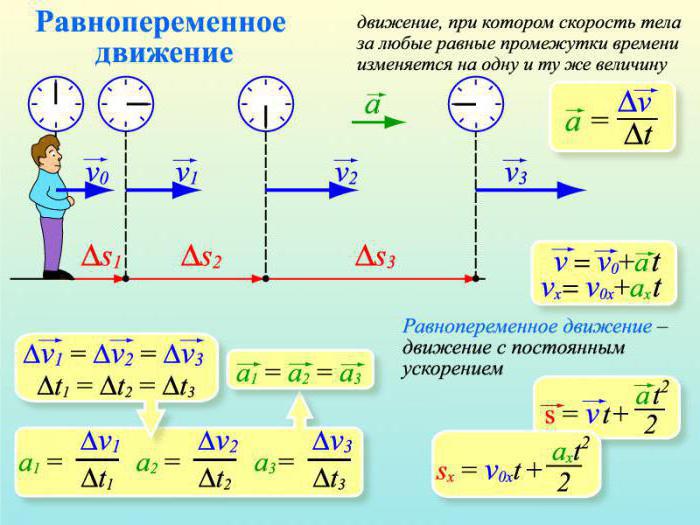
Jako příklad můžete učinit jednotně zrychlený a stejně zpomalený pohyb. Rovnoměrně zrychlený pohyb je charakterizován, jak je dobře známo, zrychlením těla. Zrychlení zůstává konstantní, ale rychlost se neustále zvyšuje v každém jednotlivém okamžiku. A při stejně pomalém pohybu má zrychlení zápornou hodnotu, rychlost těla se neustále snižuje. Tyto dva typy akcelerace jsou základem mnoha fyzikálních problémů a často se vyskytují v problémech první části testů ve fyzice.

Příklad rovnoměrně zrychleného pohybu

Stejně zrychlený pohyb se setkáváme všude všude. Žádné auto se v reálném životě nerovná rovnoměrně. Dokonce i když rychloměr ukazuje přesně 6 kilometrů za hodinu, mělo by být pochopeno, že tomu tak není. Nejprve, pokud analyzujeme tento problém z technického hlediska, první parametr, který poskytne nepřesnost, bude zařízení. Spíše jeho chyba.

Setkáváme se s nimi ve všech přístrojové vybavení. Stejný řádek. Vezměte asi deset kusů přinejmenším stejných pravítků (například 15 cm), ačkoli odlišných (15, 30, 45, 50 centimetrů). Připojte je navzájem a zjistíte, že existují malé nepřesnosti a jejich váhy se zcela neshodují. To je chyba. V tomto případě se bude rovnat polovině ceny rozdělení, stejně jako u ostatních nástrojů, které vytvářejí určité hodnoty.

Druhým faktorem, který dává nepřesnost, je měřítko zařízení. Tachometr nezohledňuje hodnoty, jako je půl kilometru, jeden druhý kilometr a tak dále. Upozornění na zařízení je oko těžké. Téměř nemožné. Ale dochází ke změně rychlosti. Pusťte na tak malé množství, ale stále. Tím bude rovnoměrně zrychlený pohyb a nebude jednotný. Totéž lze říci o obvyklém kroku. Pojďme, řekněme, chodíme a někdo říká: naše rychlost je 5 kilometrů za hodinu. Ale to není úplně pravda, a proč to bylo řečeno o něco výš.

Zrychlení těla

Zrychlení může být pozitivní a negativní. To bylo zmíněno dříve. Přidáváme, že akcelerace je vektorová veličina, která se číselně rovná změně rychlosti během určitého časového období. To znamená, že prostřednictvím vzorce může být označen následujícím způsobem: a = dV / dt, kde dV je změna rychlosti, dt je časový interval (změna času).

Nuance

Bezprostředně se může stát otázka, jak může být zrychlení v této situaci negativní. Ti lidé, kteří položí podobnou otázku, to motivují skutečností, že i rychlost nemůže být negativní, ne tentokrát. Ve skutečnosti nemůže být čas skutečně negativní. Je však často zapomenuto, že rychlost může mít negativní hodnoty. Toto je vektorové množství, nezapomeňte na to! Celá věc, pravděpodobně, ve stereotypech a nesprávném myšlení.

Abychom řešili problémy, stačí pochopit jednu věc: zrychlení bude pozitivní, pokud tělo urychlí. A bude to negativní, pokud tělo zpomalí. To je vše, dost jednoduché. Nejjednodušší logické myšlení nebo schopnost vidět mezi linkami bude ve skutečnosti součástí řešení fyzického problému týkajícího se rychlosti a zrychlení. Zvláštním případem je gravitační zrychlení a to nemůže být negativní.

Vzorce. Řešení problémů

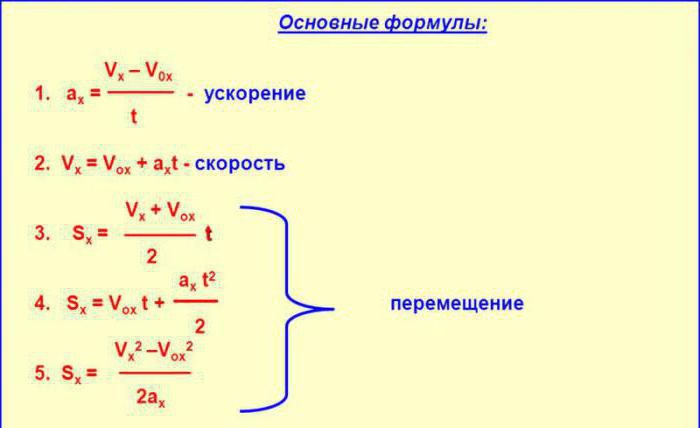
Je třeba si uvědomit, že úkoly spojené s rychlostí a zrychlením jsou nejen praktické, ale i teoretické. Proto je budeme analyzovat a pokud je to možné, pokusíme se vysvětlit, proč je tato odpověď správná nebo naopak špatná.

Teoretický problém

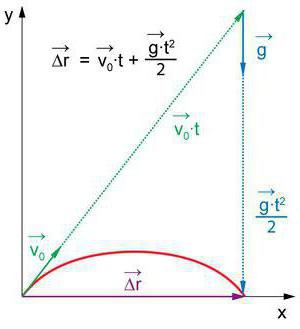
Velmi často se ve zkouškách ve fyzice v 9. a 11. třídě setkáváme s těmito otázkami: "Jak se bude chovat, jestliže součet všech sil působících na něm bude nulový?". Ve skutečnosti může být znění otázky velmi odlišné, ale odpověď je stále stejná. První věc, kterou musíte udělat, je začít s povrchovými budovami a běžným logickým myšlením.

Výběr studenta má 4 odpovědi. Za prvé: "rychlost bude nula". Druhý: "rychlost těla klesá po určitou dobu". Za třetí: "rychlost těla je konstantní, ale není to přesně nulová". Za čtvrté: "rychlost může mít jakoukoli hodnotu, ale v každém okamžiku bude konstantní."

Správná odpověď je samozřejmě čtvrtá. Nyní uvidíme proč. Zkusme zvážit všechny možnosti. Jak je známo, součet všech sil působících na tělo je součinem hmotnosti a zrychlení. Ale hmota zůstává konstantní, my ji odhodíme. To znamená, že pokud je součet všech sil nulový, zrychlení bude také nulové.

Předpokládejme tedy, že rychlost bude nula. Ale to nemůže být, protože máme nulovou akceleraci. Čistě fyzicky je to přípustné, ale ne v tomto případě, protože teď mluvíme o něčem jiném. Nechte rychlost těla klesat po určitou dobu. Ale jak se může snížit, pokud je zrychlení konstantní a je nulová? Neexistují žádné důvody a předpoklady pro snížení nebo zvýšení rychlosti. Proto odmítáme druhou možnost.

Předpokládejme, že rychlost těla je konstantní, ale není to přesně nulové. Opravdu bude konstantní kvůli tomu, že zrychlení prostě chybí. Ale nemůžeme s jistotou říci, že rychlost se bude lišit od nuly. Ale čtvrtá možnost - přímo v jablku. Rychlost může být libovolná, ale protože není žádné zrychlení, bude časově konstantní.

Praktický úkol

Zjistěte, kterou cestou tělesa prošlo v určitém časovém období t1-t2 (t1 = 0 sekund, t2 = 2 sekundy), pokud jsou k dispozici následující údaje. Počáteční rychlost těla v intervalu od 0 do 1 sekundy je 0 metrů za sekundu, konečná rychlost je 2 metry za sekundu. Rychlost těla v čase 2 sekundy se rovná také 2 metru za sekundu.

Řešení podobného problému je poměrně jednoduché, stačí jen pochopit jeho podstatu. Takže musíte najít cestu. No, pojďme ji hledat po výběru dvou oblastí. Je snadné vidět, že první část cesty (od 0 do 1 sekundy) prochází tělem rovnoměrně zrychleně, což svědčí o zvýšení jeho rychlosti. Pak najdeme toto zrychlení. Může být vyjádřeno jako rozdíl rychlostí vydělený časem pohybu. Zrychlení bude (2-0) / 1 = 2 metry za sekundu.

Podle toho bude vzdálenost ujetá na prvním rameni cesty S rovna: S = V0t + při ^ 2/2 = 0 * 1 + 2 * 1 ^ 2/2 = 0 + 1 = 1 metr. Ve druhé části cesty v období od 1 sekundy do 2 sekund se tělo pohybuje rovnoměrně. Proto se vzdálenost bude rovnat V * t = 2 * 1 = 2 metry. Nyní se shrneme vzdálenosti, dostaneme 3 metry. To je odpověď.