Vektor. Co je vektor?

Taková koncepce vektoru je zvažována téměř ve všech přírodních vědách a může mít zcela odlišné významy, a proto není možné poskytnout jedinečnou definici vektoru pro všechny oblasti. Ale zkusme to na to přijít. Takže co je vektor?

Pojem vektor v klasické geometrii

Vektor v geometrii je segment, pro který je označen, který z jeho bodů je začátek a který je konec. To znamená, že je jednodušší, vektor je řízený segment.

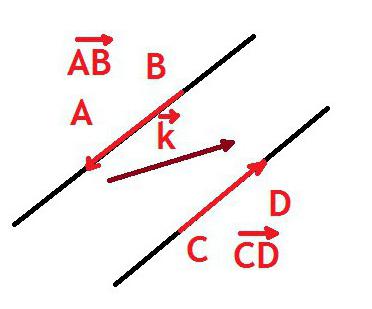
Podle toho je vektor označen (co je považováno výše), stejně jako segment, tj. Dva velkými písmeny Latinská abeceda s pomlčkou nebo šipkou směřující vpravo shora. Můžete také jej podepsat malým písmenem (latinská abeceda) s pomlčkou nebo šipkou. Šipka je vždy směrována doprava a nemění se v závislosti na umístění vektoru.

Takže vektor má směr a délku.

Označení vektoru obsahuje jeho směr. Toto je vyjádřeno jako na obrázku níže.

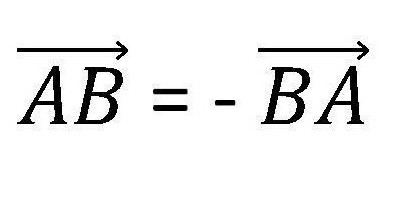
Změna směru mění hodnotu vektoru naopak.

Délka vektoru je délka segmentu, ze kterého je vytvořen. Označuje se jako modul vektoru. To je znázorněno na obrázku níže.

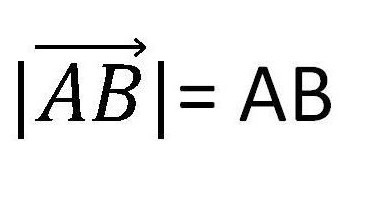
V souladu s tím je nula vektor, jehož délka je nula. Z toho vyplývá, že nulový vektor je bod a body počátku a konce se v něm shodují.

Délka vektoru - hodnota není vždy záporná. Jinými slovy, pokud existuje segment, pak má nutně určitou délku nebo je bod, pak je jeho délka rovna nule.

Pojem bod je základní a nemá definici.

Vektorové doplnění

Existují speciální vzorce a pravidla pro vektory, které můžete přidat.

Pravidlo trojúhelníku. Pro vektorové přírůstky podle tohoto pravidla stačí kombinovat konec prvního vektoru a začátek druhého, při použití paralelního překladu a připojit je. Výsledný třetí vektor se rovná přidání dalších dvou vektorů.

Pravidlo pro paralelogram. Pro přidání podle tohoto pravidla je nutné nakreslit oba vektory z jednoho bodu a nakonec nakreslit další vektor od konce každého z nich. To znamená, že druhá bude čerpána z prvního vektoru a první z druhého. Výsledkem je nový průsečík a vzniká rovnoběžník. Pokud spojíme průsečík počátků a konců vektorů, výsledný vektor bude výsledkem přidání.

Podobně je možné provést a odečíst.

Vektorový rozdíl

Podobně jako vektorové doplnění je možné je odečíst. Je založen na principu uvedeném na následujícím obrázku.

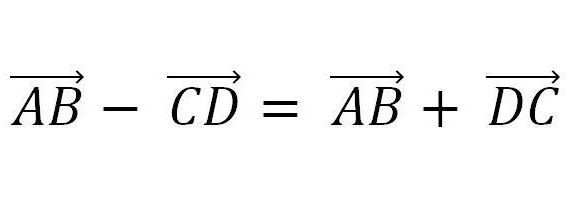
To znamená, že stačí reprezentovat odečtený vektor ve formě vektoru, naopak, a vypočítat podle principů přidání.

Také absolutně jakýkoli nenulový vektor může být vynásoben libovolným počtem k, změní se jeho délka k časy.

Navíc existují další vzorce vektorů (například vyjádření délky vektoru přes jeho souřadnice).

Umístění vektorů

Jistě, mnozí byli konfrontováni s takovou koncepcí jako kolineární vektor. Co je to kolinearita?

Kolinearita vektorů je ekvivalentní rovnoběžným liniím. Pokud dva vektory leží na rovných liniích, které jsou vzájemně rovnoběžné nebo na jedné přímce, pak se tyto vektory nazývají kolineární.

Směr Vzájemně vůči sobě mohou být kolineární vektory koordinovány nebo opačně zaměřeny, to je určeno směrem vektorů. Proto je-li vektor společně s jiným, potom je protilehlý vektor proti sobě nasměrován.

První obrázek ukazuje dva protilehlý vektory a třetí, který není pro ně kolineární.

Po zavedení výše uvedených vlastností je možné definovat a rovnat vektory - jedná se o vektory, které jsou orientovány ve stejném směru a mají stejnou délku segmentů, ze kterých jsou vytvořeny.

V mnoha vědách je také použita koncepce radiusového vektoru. Takový vektor popisuje polohu jednoho bodu roviny vzhledem k jinému pevnému bodu (často je to původ).

Vektory ve fyzice

Předpokládejme, že při řešení problému vznikla podmínka: tělo se pohybuje rychlostí 3 m / s. To znamená, že se tělo pohybuje v určitém směru v jedné přímce, takže tato proměnná bude vektorovou hodnotou. Pro řešení je důležité znát jak hodnotu, tak směr, protože v závislosti na úvaze se rychlost může rovnat 3 m / s a ​​-3 m / s.

Obecně platí, že vektor ve fyzice se používá k označení směru působení síly na tělo a k určení výsledku.

Když jsou tyto síly uvedeny na obrázku, jsou označeny šipkami s podpisem vektoru nad ním. Klasicky je délka šipky stejně důležitá, s pomocí toho označují, která síla působí silněji, ale tato vedlejší vlastnost se nestojí na tom spoléhat.

Vektor v lineární algebře a matematická analýza

Prvky lineárních prostorů se nazývají také vektory, ale v tomto případě jsou uspořádaným systémem čísel popisujícími některé prvky. Proto směr v tomto případě již nemá význam. Vektorová definice v klasické geometrii a v matematická analýza se velmi liší.

Projekční vektory

Projektovaný vektor - co to je?

Poměrně často je pro správný a pohodlný výpočet nutné rozložit vektor ve dvourozměrném nebo trojrozměrném prostoru podél souřadnic. Tato operace je nutná například při mechanickém výpočtu sil působících na tělo. Vektor ve fyzice se používá poměrně často.

Chcete-li provést projekci, stačí snížit kolmo od začátku a konce vektoru na každou z os souřadnic, segmenty získané na nich budou nazývány projekcí vektoru na osu.

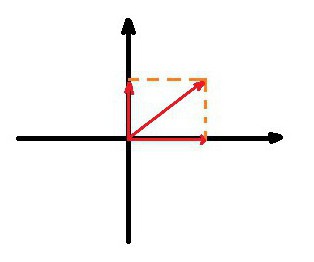
Pro výpočet délky projekce stačí vynásobit počáteční délku určitou trigonometrickou funkcí, která se získá vyřešením mini-problému. V podstatě je pravý trojúhelník ve kterém hypotenze je původní vektor, jedna z nohou je projekce a druhá je sestupná kolmice.