Co je to predikát: definice a příklady

Co je to predikát? Toto slovo se nachází v lingvistice, matematice, filozofii a programování. Ale nemůže to být tak, že v těchto velmi odlišných vědách má toto slovo stejný význam? Matematická logika dává svou vlastní speciální interpretaci tohoto pojmu. Začněme s tím.

Predikát v matematice

V matematické logice je predikát obvykle chápán jako funkce P: X → {true, false}, nazývaný predikát X. Nicméně, predikáty mají mnoho různých aplikací a interpretací v matematice a logice a jejich přesná definice, význam a použití se bude lišit od teorie k teorii. Takže například pokud teorie definuje koncept vztahu, pak je predikát jednoduše charakteristickou funkcí, jinak známou jako indikátorová funkce vztahu. Nicméně ne všechny teorie jsou příbuzné nebo založené na teorii množin, takže musíte být opatrní se správnou definicí a sémantickou interpretací predikátu.

Pravda nebo nepravda

Pokud stále nerozumíte tomu, co je předpoklad v matematice, pak stojí za to podrobněji se zabývat. Neformálně je predikát výrok, který může být pravdivý nebo nepravdivý, v závislosti na hodnotách jeho proměnných. Může být myšlenka jako operátor nebo funkce, která vrátí hodnotu, která je pravdivá nebo nepravdivá. Například předikáty se někdy používají k zadání sady prvků: když mluvíme o sadách, je někdy nepohodlné nebo nemožné popsat soubor tím, že uvede všechny jeho prvky. Předpoklad P (x) tedy bude pravdivý nebo nepravdivý, v závislosti na tom, zda x patří k sadě.

Vlastnosti objektu

Předpovědi v matematické logice jsou také široce používány k tomu, aby mluvily o vlastnostech objektů a definovaly soubor všech objektů, které mají společnou vlastnost. Takže například když P je predikát X, někdy lze říci, že P je vlastnost X. Podobně se označuje P (x) jako věta nebo prohlášení P vzhledem k objektu proměnné X. Soubor definovaný písmenem P (x) je napsán jako { x | P (x)} a je množina objektů, pro které platí P.

Například {x | x je kladné celé číslo menší než 4} je množina {1,2,3}.

Pokud t je prvkem množiny {x | P (x)}, potom příkaz P (t) je pravdivý.

Zde se P (x) nazývá predikát a x je zástupný symbol. Někdy je P (x) také nazývána propositional funkce, protože každá volba s X vytvoří větu.

Jednoduchá forma predikátu (P) je booleovský výraz a v tomto případě jsou vstupy do výrazu sami kombinovány s booleovskými operacemi. Booleovský výraz s předikovanou pravdou je složitější jev.

Formální definice

• Přesná sémantická interpretace atomového vzorce a atomového věty se bude lišit od teorie k teorii.
• V propoziční logice se atomové vzorce nazývají propoziční proměnné. V jistém smyslu jsou to předikáty s nulovými hodnotami.
• V logice prvního řádu se atomový vzorec skládá z předikátového symbolu, který je aplikován na odpovídající počet členů.
• V teorii množin jsou predikáty chápány jako charakteristické funkce nebo definují funkce indikátoru, tj. Funkce z daného prvku na hodnotu pravdy.
• Metoda sestavování typů soudů používá predikáty k jejich určení.
• V auto-epistemické logice, která odmítá zákon vyloučeného středu, mohou být predikáty pravdivé, falešné nebo prostě neznámé, to znamená, že tato sada skutečností nemusí být dostatečná k tomu, aby určila pravdu nebo falešnost předikátu.
• V fuzzy logice jsou predikáty charakteristickými funkcemi distribuce pravděpodobnosti. To znamená, že přísný pravdivý / nepravdivý odhad predikátu je nahrazen hodnotou interpretovanou jako stupeň pravdy.

Gramatika Predikát

Ve teoretických teoriích gramatiky existují dva konkurující koncepty predikátů. Konkurence mezi těmito dvěma koncepty vyvolala zmatek ohledně použití termínu "predikát" v teoretických teoriích gramatiky. Takže co je predikát? Tento článek zahrnuje oba tyto pojmy.

První koncept se týká tradiční gramatiky, která má tendenci považovat predikát za jednu ze dvou hlavních částí věty, druhou je předmět. Účelem predikátu je dokončit myšlenku subjektu, například co dělá nebo co to je.

Druhý koncept byl odvozen z práce v predikátovém počtu (predikátová logika, logika prvního řádu) a je prominentní v moderních teoriích syntaxe a gramatiky. V tomto přístupu předikát věty v podstatě odpovídá hlavnímu slovesu a všem pomocným prostředkům, které doprovázejí hlavní sloveso. Současně její argumenty (například fráze podstatného jména) jsou mimo predikát.

V tradiční gramatice

Koncept P v tradiční gramatice je inspirován proposiální logikou starověku (na rozdíl od modernější logiky predikátů). Předikát je považován za vlastnost, kterou má subjekt. Proto je predikát výrazem, který může být pravdivý. Tak, výraz "pohyby" je pravdivý pro všechno, co se pohybuje. To dává odpověď na otázku, co je predikát.

Takové klasické porozumění predikátů bylo přijato více či méně přímo v latinských a řeckých gramatikách a odtud se dostalo do gramatiky anglického a ruského jazyka, kde se aplikuje přímo na analýzu struktury věty. Toto porozumění P ​​je také používáno v angličtině-slovní slovníky.

Předmět a predikát

Predikát je jedna ze dvou hlavních částí věty (druhá je předmět, který modifikuje predikát). Musí obsahovat sloveso a sloveso vyžaduje nebo dovoluje ostatním prvkům vyplnit predikát.

Předikát poskytuje informace o předmětu: co to je, co dělá subjekt nebo co je objekt. Spojení mezi předmětem a jeho predikátorem se někdy nazývá jazykem predikátů. Jeho nominální hodnota je podstatná fráze. Například ve větě "George III - král Anglie" je král Anglie přednostní nominální. Předmět a prediktivní hodnota musí být spojena spojovacím slovesem, nazývaným také copula. Předmět a přívlastkové přídavné jméno musí být také spojeny.

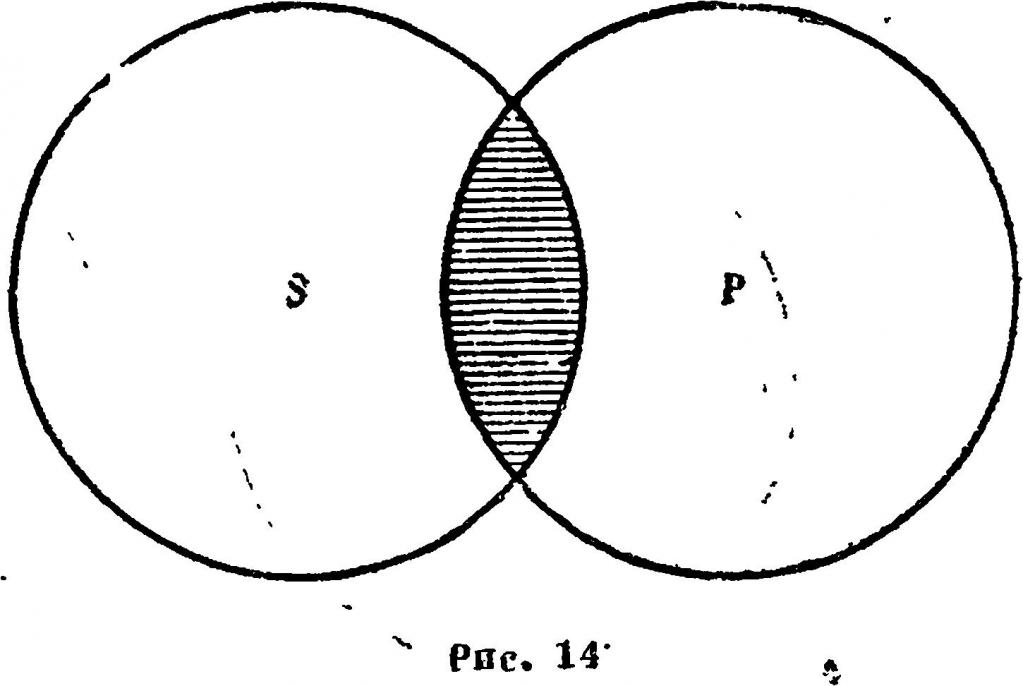
Ve syntaxi

Syntaktická P označuje syntaktickou platnost použití díla ve formální gramatice a je podobná sémantickému predikátu, který určuje sémantickou realitu aplikace díla. Ve své první implementaci měly syntaktické predikáty tvar "(α)?" A mohly se objevit pouze na levém okraji díla. Nezbytnou syntaktickou podmínkou α může být libovolný platný kontext bez gramatiky.

Formálněji syntaktický predikát je forma průniku výroby použitá v specifikacích parseru nebo ve formálních gramatikách. V tomto smyslu má pojem význam matematické funkce indikátoru. Pokud jsou p1 a p2 pravidla výroby, jazykem generovaným p1 a p2 je jejich dané křižovatce.

Reflexní gramatické výrazy (PEGs), vynalezené Brianem Fordem, rozšiřují tyto jednoduché P, které jim umožňují objevit se kdekoliv ve výrobě spolu s "non-predikáty". Navíc Ford vynalezl proces parsování pro zpracování těchto gramatik v lineárním čase.

Tento přístup je implementován v ANTLR verze 3, která používá deterministické státní stroje pro prohlížení. To může vyžadovat testování predikátu pro výběr mezi syntaktickými přechody (tzv. "Pre-LL (*)" parsování).

V moderních syntaktických teoriích

Většina moderních teorií syntaxe a gramatiky pochází z teorie predikátního počtu spojeného s Gottlobem Fregem. Toto pochopení vidí predikáty jako vztahy nebo funkce, které stojí nad argumenty. Používají se buď k přiřazení vlastností k jednomu argumentu nebo ke vzájemnému propojení dvou nebo více argumentů. Návrhy se skládají z predikátů a jejich argumentů (a dodatků) a jsou tedy struktury argumentu predikátu. V souladu s nimi je toto P považováno za propojení jeho argumentů s větší strukturou.

Predikáty jsou umístěny vlevo mimo závorky, zatímco jejich argumenty jsou umístěny uvnitř hranatých závorek. Jeden rozpoznává predikovanou valenci, podle níž může být k dispozici (není zobrazeno), monovalentní, bivalentní nebo trojmocné. Tyto typy reprezentací jsou podobné formálním sémantickým analýzám, kde mluvíme o správném zachycení skutečností kvantifikátorů a logických operátorů. Nicméně, pokud jde o základní strukturu věty, tyto myšlenky předpokládají především to, že slovesa jsou predikáty a fráze podstatného jména, s nimiž se objevují, jsou jejich argumenty. S tímto chápáním věty je binární dělení věty na předmět NP a predikát VP jen stěží možné. Místo toho je sloveso predikát a podstatná jména jsou jeho argumenty.

V logice

Logika prvního řádu, známá také jako predikátový počet prvního řádu a predikátová logika, je soubor formálních systémů používaných v matematice, filozofii, lingvistice a informatice. Logika prvního řádu používá kvantizační proměnné nad objekty a umožňuje použití vět, které obsahují proměnné. To je odlišuje od propositional logiky, která nepoužívá kvantifikátory nebo vztahy.

Logika prvního řádu

Takové teorie jsou zpravidla součástí logiky prvního řádu spolu s určitou oblastí diskurzu, v níž se mění kvantifikované proměnné. Někdy je teorie chápána ve formálnějším smyslu, a to je jen sada vět v prvotřídní logice.

Použité adjektivy rozlišují logiku prvního řádu od logiky vyššího řádu, ve které existují "definování predikátů nebo funkcí jako argumentů nebo v nichž jsou povoleny jeden nebo oba kvantifikátory predikátů nebo kvantifikátory funkcí. V teoriích prvního řádu jsou predikáty často spojovány se soubory. Ve vyšších pořadí interpretibilních teorií lze interpretovat jako množiny. Něco podobného se používá při definici predikátu v programování. To není překvapující, protože matematika se stala jakousi surovinou pro tuto vědu.

Teoretická část

Existuje mnoho deduktivních systémů pro typy soudů a logiku prvního řádu, které jsou oba zvuky (všechny prokazatelné příkazy jsou pravdivé ve všech modelech) a kompletní (prohlášení, která jsou pravdivá pro všechny modely, jsou prokazatelné). Přestože vztah logického důsledku je jenom částečně rozpustný, v automatizované věty se prokázal logika prvního řádu, bylo dosaženo významného pokroku. Logika prvního řádu také splňuje několik metalogických vět, která ji činí vhodnou pro analýzu v teorii důkazů, jako je věta Levenheim-Skolem a věta kompaktnosti.

Logika prvního řádu je standardem pro formalizaci matematiky v axiomech a je studována v základech matematiky. Peano aritmetika a Zermelo-Fraenkelová teorie množin jsou axiomatizace teorie čísel a teorie množin, resp., Jsou součástí logiky prvního řádu. Nicméně teorie prvního řádu nemá schopnost jednoznačně popisovat strukturu s nekonečnou oblastí, například přirozených čísel. Systémy axiomu, které plně popisují tyto dvě struktury (tj. Kategorické axiomové systémy), lze získat v silnějších formách logiky, jako je logika druhého řádu.

Základy prvotřídní logiky byly vyvinuty nezávisle od Gottlob Frege a Charles Sanders Pierce.