Co to je - kužel v geometrii. Rovný kužel s kulatou základnou a jeho charakteristikami

Prostorová geometrie, jejíž průběh probíhá na střední škole, zkoumá vlastnosti a vlastnosti různých geometrických tvarů ve třech rozměrech. Jedním z takových známých postav je kužel. To, že to je kužel, jaké prvky popisuje a jaké vlastnosti má, článek zodpoví tyto otázky.

Kužel v geometrii

Z hlediska stereometrie je kuželem postava vytvořená ve vesmíru spojením přímých segmentů určitého bodu s křivkou v rovině. Tato křivka se nazývá directrix nebo průvodce. To omezuje tvar základny. Directrix může být uzavřená čára, například elipsa nebo kruh, nebo nemusí být uzavřena jako hyperbola nebo parabola. Všechny segmenty, které propojují direktivu s výše uvedeným bodem prostoru, se nazývají generátory nebo generátory. Sada generátorů definuje kuželový povrch a bod, ze kterého vystupují, se nazývá vrchol kužele.

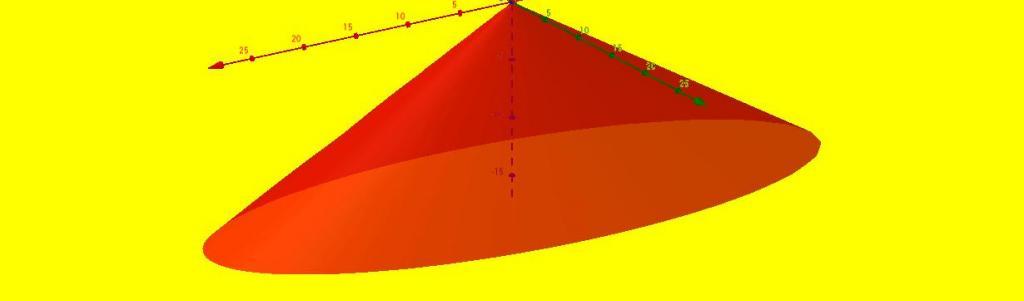
Kužel je tedy postava, která má jeden vrchol, bez okrajů a skládá se ze dvou povrchů (plochá základna a boční kuželovitý povrch). Eliptický kužel je znázorněn na obrázku výše.

Kruhový nebo kulatý kužel

Pod pojmem "kolo" v názvu položky rozumíte číslo, jehož základem je kruh. Na rozdíl od ostatních typů kužele může být v důsledku otáčení získána kulatá postava. Níže uvedený obrázek demonstruje tento proces.

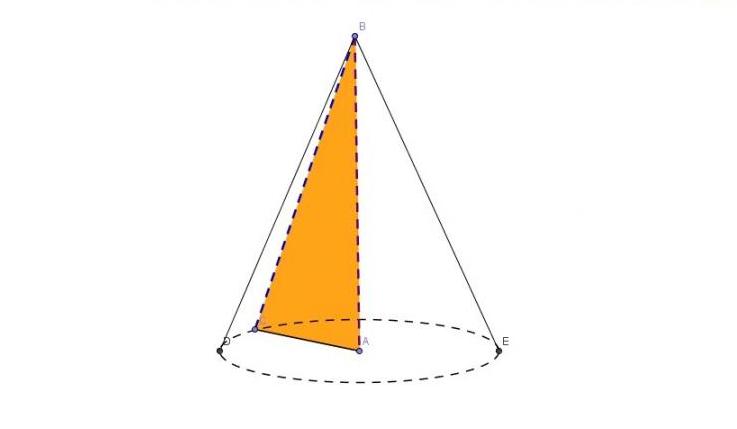
Dovolte nám stručně vysvětlit, co ukazuje obrázek. Trojúhelník ABC je obdélníkový. Pokud se otočí kolem nohy AB, noha AC bude popisovat jeden povrch kužele, základny a hypotenze BC bude mít za následek vytvoření kónického povrchu v důsledku otáčení.

Kónus zobrazený na obrázku není pouze kulatý, ale rovný. Poslední vlastnost je důležitá při výpočtu lineárních parametrů, plochy a objemu obrázku.

Geometrický tvar kužele je přímý, pokud výška h spadá přesně do středu základny (v tomto případě je výška segmentu AB a střed základny je bod A). Není-li splněná podmínka splněna, je číslo nazýváno šikmo. Šikmé a rovné kužele jsou zobrazeny níže pro přehlednost.

Mnoho objektů, které nás obklopují, jako jsou kuželky zmrzliny, pruhovaný silniční kužel nebo nálevka pro nalévání kapaliny přes úzké otvory, mají tvar kužele s kruhovou základnou.

Dále zvažujeme kvantitativní charakteristiky přímého kužele s kruhovou základnou.

Lineární rozměry postavy a úhel na základně

Lineární rozměry kužele jsou sada parametrů, které vám umožňují jednoznačně definovat číslo v prostoru. Jedná se o následující:

• poloměr základny r;
• výška h;
• generatrix g.

Všimněte si, že pro daný typ kužele jsou všechny generátory stejné a protínají základnu obrázku ve stejném úhlu.

Vedle výše uvedených lineárních parametrů je kužel také charakterizován úhlem φ mezi generátorem a základnou.

Všechny tyto charakteristiky jsou vzájemně propojeny těmito základními rovnicemi:

g = √ (h ² + r ² );

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ)

Tyto rovnosti mohou být psány nezávisle, pokud vezmeme v úvahu pravý trojúhelník uvnitř kužele a připomínáme definice označených trigonometrických funkcí.

Plocha

Plocha základny a kuželovitý povrch je důležitou vlastností kužele. Je jasnější a jednodušší studovat povrch postavy, který není v trojrozměrném, ale ve dvourozměrném prostoru. Chcete-li to provést, proveďte tzv. Skenovací vzory. Předpokládáme, že proces přijetí je následující: Předpokládejme, že je vyroben papír z kužele. Nejprve jsme sejmuli základnu podél obvodu a pak jsme vyřízli kuželovou plochu podél generátoru a rozvinuli jej. Obdrželi jsme skenování kužele, které je znázorněno na obrázku níže.

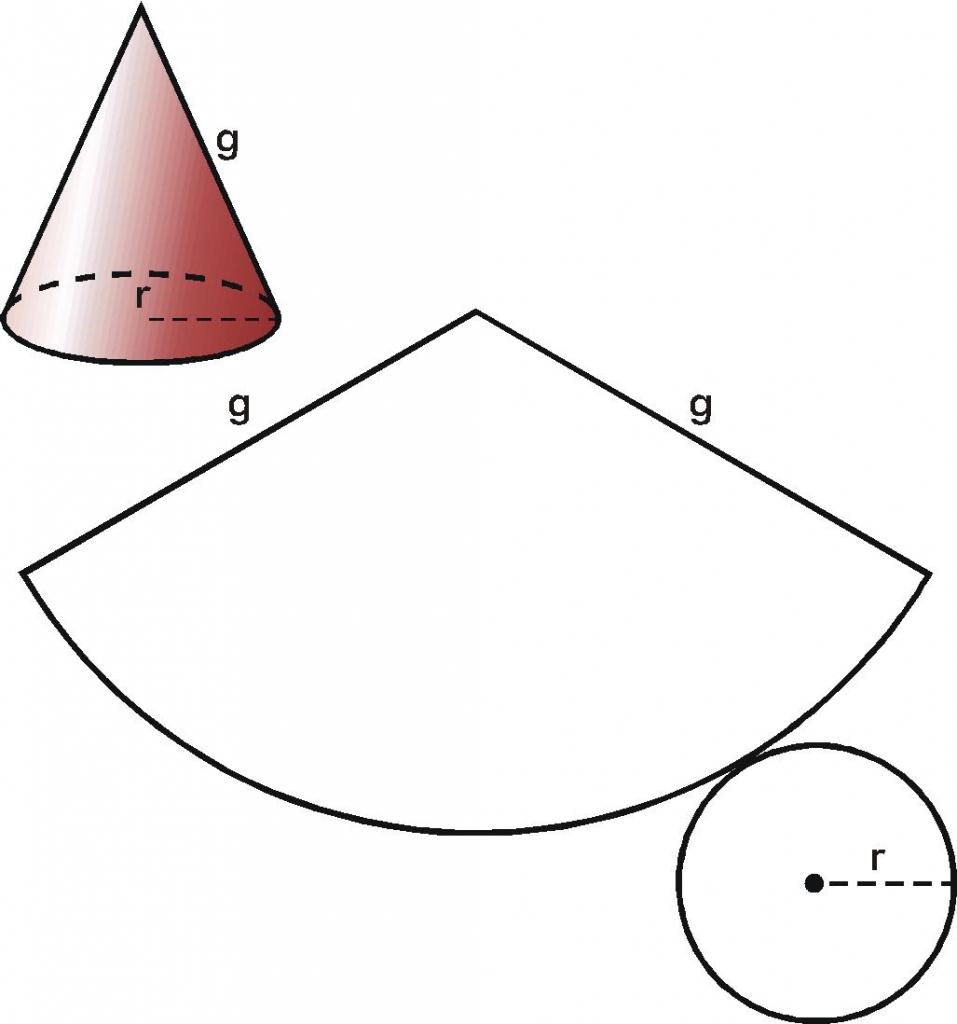
Plocha celého zametání S se rovná:

S = S _o + S _b

Kde první termín (S _o ) je oblast kruhu, druhý termín (S _b ) je oblast kruhového sektoru odrážejícího kuželový povrch. Hodnota S _{o se} vypočte podle následujícího vzorce:

S _o = pi * r ²

S kruhovým sektorem je situace komplikovanější. To je ohraničeno dvěma poloměry, jejichž délka je rovna generátoru g a jeden oblouk odpovídá obvodu základního kruhu. Tyto číselné informace umožňují jednoznačně určit oblast odvětví. Nebudeme jít do matematických výpočtů, ale budeme okamžitě dávat finální vzorec pro S _b :

Sb = pi * r * g

Srovnání písemných vzorců pro Sb a S _o naznačuje, že boční plocha je vždy větší než plocha báze g / r.

Vzorec pro celkovou plochu povrchu je následující:

S = pi * r * (r + g)

Velikost těla

Kužel je prostorová postava, takže má určitý objem. Číselně odpovídá prostoru prostoru, který je ohraničen kuželovou plochou a kruhovou základnou. K určení objemu kužele použijte následující výraz:

V = 1/3 * S _o * h

Nahrazením tohoto výrazu formulacem pro S _o dostaneme:

V = 1/3 * pi * r ² * h

Někteří čtenáři si možná všimli, že vzorec pro objem kužele odpovídá vzorci pro pyramidu. Tato náhoda není náhodná, protože tvary těchto čísel se stanou shodnými, jestliže počet okrajů přímky pyramidy stoupá do nekonečna.