Co je systém egyptských čísel? Historie, popis, příklady

S neposlušným systémem egyptských čísel, který byl použit ve starověkém Egyptě, jsme vizuálně obeznámeni s několika zbývajícími papyrusy. Příklady úkolů a jejich řešení jsou v nich tak zajímavé, že zbývá jen litovat, že je jen málo z nich.

Z nich je zřejmé, že matematika a systém egyptských čísel úzce souvisí s ekonomickými potřebami a praktickou aplikací. Každý rok po povodni Nilu bylo nutné obnovit stavby, znovu vyložit pozemky, vypočítat plochu a hranice, uchovat záznam o sklizni, kalendáři.

Co je poziční a neposlušné číslované systémy?

Odpověď spočívá v názvu samotném. Pokud pozice číslice ovlivňuje výsledek výpočtů, máme polohový systém čísel, pokud ne - polohový.

Pokud píšeme 12, je to dvanáct, a se stejnými čísly, 21 je dvacet jedna. Podle egyptského číselného systému: abyste napsali 12, musíte použít symbol jednotky dvakrát a symbol desítek jednou a 21 bude vypadat jako jeden symbol jednotky a dva desítky symbolů, to znamená, stačí napsat tři symboly.

Nepořazené jsou: římský systém, který je nám známý, v němž čísla jsou označena římskými písmeny, slovanským systémem, kde každý dopis označuje také určité číslo nebo číslo. Římský systém zvládl své funkce v západní Evropě až do 16. století.

Systém čísel, který používáme v moderním životě, je polohový desítkový systém.

Nonpositional systémy byly vhodné pro provádění jednoduchých aritmetických operací, protože složité výpočty zahrnovaly těžkopádné záznamy, které nezabránily úspěšnému rozvoji algebry a geometrie ve starověkém Egyptě.

Jak si Egypťané mysleli?

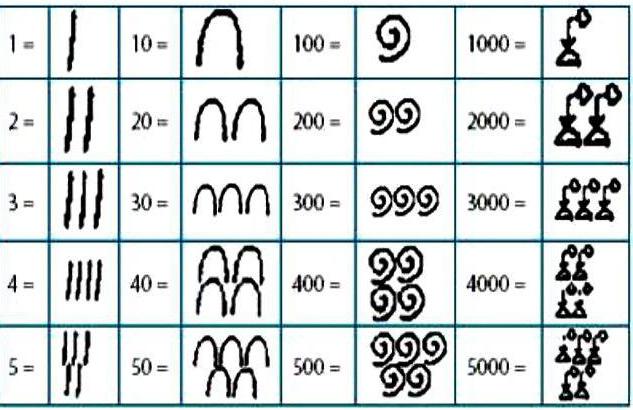
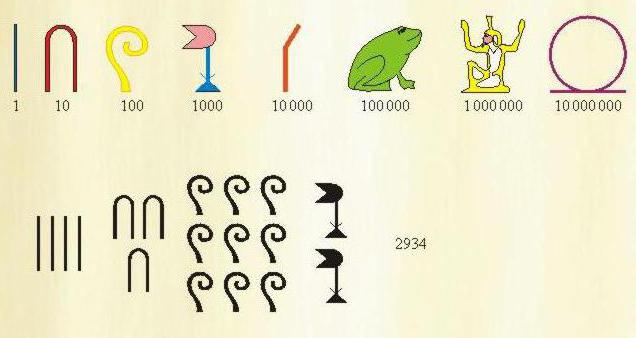
Co je to - systém egyptských čísel? Abychom mohli napsat libovolné číslo, použili jsme hieroglyfy označující určitá čísla, jejichž součet se rovnal požadované hodnotě.

Zvláštní označení bylo k dispozici pro čísla 1, 10, 100, 1000, 10000, 100000, 1000000. Při psaní požadovaného čísla bylo každé označení používáno až 9krát. Záznam v egyptském číselném systému byl ve vzestupném pořadí: nejprve jednotky, pak desítky, stovky a tak dále.

A psali zpravidla zprava doleva, ale to bylo možné zleva doprava, množství tohoto se nezměnilo. Bylo také použito vertikální psaní, ale pak odpočítávání šlo zhora dolů.

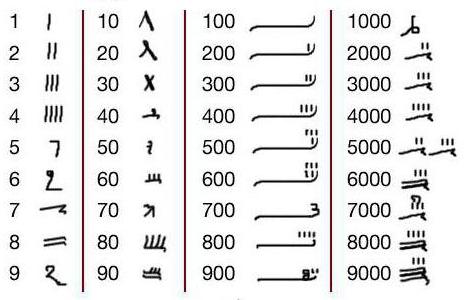
Byly použity dva způsoby psaní:

1. Hieroglyphic, v němž byly použity přijaté hieroglyfy.
2. Hieratic, což bylo praktičtější a praktičtější.

Prohlídka historie

Historie egyptského číselného systému pochází z dávných dob, první rukopisy s čísly se týkají druhého tisíciletí před naším letopočtem. Pak nebyly žádné peníze, takže systém byl používán jak pro neuvěřitelnou složitost a velikost matematických problémů, tak pro řešení každodenních každodenních problémů.

Koneckonců znalost matematiky byla použita v zememeračním průzkumu a v budování kalendářů a map v astronomii, navigaci a při stavbě paláců, kanálů a vojenských opevnění.

Egypťanský systém nepozičních čísel byl používán až do 10. století.

Má také mystický význam, jehož tajemství kněží s sebou, ale částečně otevřel svět Pythagoras. Má díla, ve kterých popisuje symbolické významy, které jsou dány digitálním hieroglyfům, které napsal po jeho pobytu v Egyptě. Proto jejich popis patří do systému egyptských čísel.

Jen pár papyrů z těchto časů přežilo, čímž lze pochopit, že úroveň matematiky byla vysoká. Je věrohodné, že Řekové studovali starou egyptskou matematiku. Jedním z nejvnitřnějších poznatků je egyptský systém bez polohových čísel.

Papyrus Ahmes

Akhmes Papyrus pochází z roku 1650 př.nl, obsahuje 84 matematických úkolů. To bylo nalezeno v Thébách, uložené v Britském muzeu.

Všechny úkoly v papyru jsou zváženy na konkrétních příkladech systému egyptských čísel. Zobrazují příklady výpočtů s frakcemi, s celistvými čísly, dělením a násobením.

Výpočty jsou uvedeny pro nalezení oblastí geometrických tvarů: čtyřúhelník, kruh, trojúhelník.

Informace z papyru dokazují, že egyptští matematici byli schopni extrahovat kořen, dělat aritmetické a geometrická progrese rovnice s neznámými.

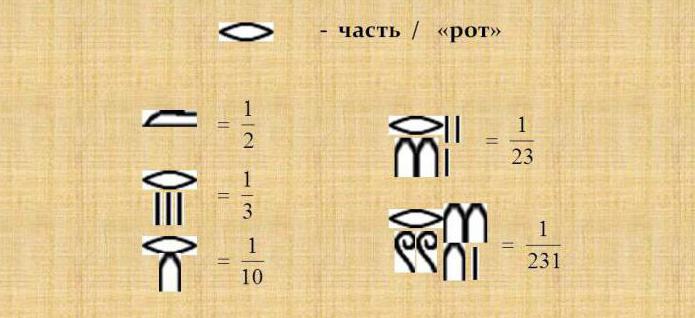
Podíl alikvot

Je zajímavé, že ve výpočtech byly použity pouze alikvotní frakce, ve kterých byl čitatel roven jedné a byl označen takovým znaménkem a hodnoty jmenovatele byly zapsány pod ním a všechny ostatní frakce pro výpočty nejprve musely být expandovány do alikvotních frakcí. Ale byly používány a měly zvláštní označení frakce 2/3 a 3/4.

Aby bylo obvyklé frakce v alikvotním stavu na egyptském číselném systému, bylo nutné pracovat:

4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2 + 1/4 + 1/20

2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28

3/7 = 12/28 = 24/56 = 14/56 + 7/56 + 3/56 = 1/4 + 1/8 + 1/18 + 1/56.

Frakce byly vytvořeny moderním způsobem: snížením na společného jmenovatele, pro mnohé hodnoty existovaly četné hotové stoly.

Násobení

Egypťané se naučili požadovaný výsledek, protože nevěděli násobící tabulku, ale s použitím vědomí, že pokud se jeden faktor zdvojnásobí a druhý faktor se sníží, výsledek se nezmění:

32 * 13 = 16 * 26 = 8 * 52 = 4 * 104 = 2 * 208 = 1 * 416

Je zajímavé, že tato metoda násobení byla známá v Rusku a věřilo se, že pochází ze starověkého Egypta a v Evropě se nazývala ruština.

Papyrus Golenishčev

Díky úsilí vědce egyptologa V. S. Golenischeva, papyrus je uložen v Moskvě o 200 let starší než papyrus pisárovi Ahmse. Vědec ji koupil během své práce v Thébách.

Byl napsán hieraticky, kurzívou se zabývá 25 problémy, jejich popisem podle egyptského číselného systému a řešení. Její délka je více než 5 m a šířka 7 cm. K těmto problémům nejsou žádné připomínky, stejně jako v předchozím papyru, existují pouze matematické výpočty.

Ukazuje, že Egypťané byli schopni vypočítat oblasti trojúhelníku, lichoběžníku, obdélníku, kruhu, stejně jako objemy pyramidy, hranolky, rovnoběžnost, válce a zkrácené pyramidy s velkou přesností a mnohé vzorce se zcela shodují s moderními.

V systému egyptských čísel bylo číslo pi 3,16, což téměř odpovídalo moderní hodnotě 3,14, ačkoli v té době byla hodnota 3 použita všude na východě.

Všechno jsou čísla

To je věřil tomu Pythagoras žil v Egyptě pro 22 roků, hluboce studovat geometrii, filozofii, mysticismus čísel. Ty objevy, které později vyrobila pythagoreská škola, by se daly vytvořit ve starověkém Egyptě.

Proto se věří, že díla Pythagoras o mysticismu čísel, které později napsal, jsou založeny na tajných poznatcích, které získal od egyptských kněží. Nepřijali cizince, aby studovali, a po rozhovoru s hlavním knězem se k nim přihlásil vysokým patronátem, který je považoval za hodný tajemství.

Čísla jsou živé bytosti, které odrážejí vlastnosti prostoru, hudby, energie. Vše lze vyjádřit pomocí matematiky, popisující viditelné jevy s formulemi, předvídat neviditelné, založené na logických a matematických zákoních.

Výška, šířka základny, úhel sklonu pyramidy z Cheops v Egyptě odpovídají matematickému pravidlu pro budování pythagorské pyramidy, což také potvrzuje vztah mezi objevy, které učinil, a znalostmi získanými od starověkých egyptských kněží, kteří používali systém egyptských čísel.

Práce s čísly, starodávní myslitelé pochopili nejen podstatu věcí, ale mohli je ovlivňovat.

Při studiu matematiky starobylého Egypta pomocí egyptského číselného systému lze jen obdivovat, kolik lidí objevili tisíce let před naší dobou.