Základní zákony pro stejnosměrný proud: definice a vzorce

Ohmův zákon byl nejprve formulován německým fyzikem a matematikem Georgem Simonem Omhem. Ohmův zákon je základním zákonem pro elektrické obvody s jednosměrným proudem. Stanovuje vztah mezi napětím nebo potenciálním poklesem, proudovou silou a odporem v obvodu. Podívejme se blíže na Ohmův zákon a další základní zákony stejnosměrného proudu.

Historické pozadí

Georg Simon Om se narodil ve městě Erlangen (Německo) 16. března 1789 v protestantské rodině. Od raného dětství začal pracovat v klempířské dílně svého otce. Fyzikální kariéra začala v Omme na Polytechnické univerzitě v Norimberku. Do konce svých dnů vyučoval fyziky na Mnichovské univerzitě.

Hlavní výhodou Ohm ve fyzice je, že uvedl a popsal takovou fyzickou veličinu jako elektrický odpor. Nejprve formuloval v matematické podobě vztah mezi rozdílem potenciálů, proudem a elektrickým odporem v obvodu, pro který byla odporová jednotka pojmenována po jeho příjmení.

Ohmova nová myšlenka nebyla okamžitě přijata světovou vědeckou komunitou, teprve v roce 1841 získala Královská společnost v Londýně medaili Oom Copley a v roce 1849 mu Mnichova univerzita přidělila katedru fyziky.

Om během své vědecké činnosti se zabýval nejen elektrickými obvody. V roce 1840 studoval zvukové vlny a od roku 1852 se zabýval optikou, zejména fenoménem rušení. Vědec zemřel v Mnichově 6. července 1854.

Ohmovy experimenty

Než Om vydal svůj slavný zákon stejnosměrný proud jiní vědci provedli mnoho experimentů s elektrickými obvody. Je třeba poznamenat experimenty britského Henry Cavendish, který v roce 1781 vyšetřoval chování plechovek Leiden, ale nebyl schopen zveřejnit své závěry.

V současné době mají fyzici nástroje, které umožňují měřit všechny parametry elektrického obvodu s potřebnou přesností. Na konci 18. a počátku 19. století taková zařízení neexistovala, což způsobilo, že Ohm obtížně zjistil zákon o stejnosměrném proudu.

Proto se Om rozhodl udělat takové zařízení samo. Konkrétně použil Coulombovy torzní váhy, ale zdokonalil je přidáním magnetického prvku. Zároveň vědec použil v roce 1819 Hans Christian Oersted objev, že dirigent s proudem vyvíjí sílu na magnetizovanou jehlu v jeho blízkosti. S použitím nové torzní rovnováhy, vedení kabelů různých délek, zdroje elektrického proudu a nádob s rtuti, byl Ohm schopen měřit pokles síly, s nímž se zvětšuje délka vodiče s proudem na jehle.

V důsledku těchto experimentů vědce získal následující matematickou závislost: V = 0,41 lg (1 + x), kde V je napětí v obvodu, x je délka vodiče s proudem. Tento výraz následně vedl vědce k formulaci zákona stejnosměrného proudu.

Koncept síly elektrického proudu

Než budeme zvažovat Ohmův zákon o stejnosměrném proudu, představíme koncept současné síly. Některé částice v přírodě mají takzvaný elektrický náboj. Pojem proudové síly přímo souvisí s pohybem těchto nabitých částic, které jsou ve většině případů buď ionty nebo elektrony. Proud ve fyzice je chápán jako množství náboje, které prochází úsekem vodiče za jednotku času, což je matematicky vyjádřeno jako následující výraz: I = dq / dt.

Jednotka proudové síly v SI je ampér (A), 1 A je proudová síla, při níž se náboj 1 C přenáší vodičem po dobu 1 s. Vzhledem k tomu, že kladné a záporné náboje se pohybují v opačném směru ve stejném elektrickém poli, je obvyklé stanovit proudovou sílu ve směru pohybu kladných nábojů.

Rychlost pohybu nabitých částic v elektrickém poli

Ve fyzice je zákon stejného proudu formulován pro I = const, což znamená, že každá částice nesoucí elektrický náboj se musí pohybovat konstantní rychlostí. K tomu, aby existoval elektrický proud, je nutné mít nabité částice schopné pohybu, stejně jako existenci elektrického pole. Ten působí na elektrický náboj q s určitou silou. Tato síla je určena podle vzorce: F = q * E, zde E je intenzita elektrického pole.

Podle druhého zákona Newtonu nabitá částice získá akceleraci a = q * E / m, kde m je hmotnost částic. Protože jsou všechny hodnoty v tomto výrazu konstantní, bude zrychlení také konstantní a nenulové. Všechny tyto argumenty platí v případě, že náboj se pohybuje v prázdném prostoru, ale pokud se pohybuje v jakémkoli médiu, vzniká určitý odpor z média.

Například elektron pohybující se pod působením elektrické síly v kovovém vodiči zažívá stálé kolize s ionty vytvářejícími kovovou krystalovou mřížku. Tyto kolize způsobují, že se elektron pohybuje konstantní rychlostí, která se nazývá rychlost driftu. V interakci elektronu s ionty mřížky spočívá povaha elektrického odporu.

Pohyb elektronu v kovovém vodiči lze porovnat s pohybem dešťové kapky ve vzduchu, protože tento pokles neklesá při zrychlení volného pádu, ale způsobuje rovnoměrný pohyb vlivem vlivu odporové síly ze vzduchu.

Místní Ohmův zákon

V každé škole se začínají učit zákony DC ve třídě 8. Současně formulujte Ohmův zákon, nejprve v místní podobě. Proveďte tak například kovový vodič.

V kovu jsou valenční elektrony, tj. Elektrony umístěné na vnějších energetických skořápkách atomů, slabě vázány na atomová jádra, a proto v sypkých materiálech nepatří k určitému atomovému jádru, ale jsou svobodné nebo socializované. Každý takový elektron při pokojové teplotě se v kovovém krystalu nenápadně pohybuje. Tento pohyb je podobný pohybu molekuly v plynu. Rychlost tepelného pohybu elektronu je velká, je asi 10 ⁶ m / s. Vzhledem k tomu, že pohyb je stejně pravděpodobný ve všech směrech, nevzniká elektrický proud.

Pokud je tento vodič umístěn v elektrickém poli, objeví se proud. Výsledkem je, že elektron získává rychlost driftu, jehož velikost je ^10-6 m / s. Výsledkem je, že elektrický proud v průřezu A je zapsán následujícím způsobem: I = n * q ² * E * t * A / m _e , zde n je počet elektronů, které procházejí oblastí A v čase t, dvě elektronové kolize s mřížkovými ionty, m _e - elektronová hmota

Výsledný výraz může být přepsán jako J = I / A = σ * E, kde J je hustota elektrického proudu, σ je vlastnost materiálu, která se nazývá elektrická vodivost. Tento výraz pro proudovou hustotu se nazývá Ohmův zákon pro stejnosměrný proud v místní podobě.

Ohmův zákon v makroskopické podobě

Ve škole v platové třídě 8 je zákon o stejnosměrném proudu považován také v makroskopické podobě. Lze ji snadno získat z příslušného zákona v místní podobě. Za tímto účelem je nutné určit napětí nebo potenciální pokles elektrického obvodu v následujícím pořadí: ΔV = E * l, kde l je délka vodiče s proudem a ΔV je napětí na jeho koncích.

Výsledkem je, že Ohmův zákon bude mít formu: ΔV = I * l / (σ * A) = R * I, kde R je elektrický odpor. Jak je zřejmé ze zákona přímého elektrického proudu v makroskopické podobě, hodnota R je inverzní elektrická vodivost σ, to znamená, že čím lepší materiál vede, tím menší je jeho elektrický odpor. Je také důležité poznamenat, že zatímco σ je vlastností materiálu, ze kterého je vyroben vodič, R je vlastnost určitého vodiče a závisí nejen na materiálu, ale také na jeho geometrických parametrech (délka a průřezová oblast).

Použitelnost a význam klasického zákona Ohmu

Ohmův zákon v klasické nebo makroskopické podobě je napsán ve tvaru: V = I * R. U kovů je R konstantní hodnota, bez ohledu na pevnost proudu, který prochází vodičem. V některých materiálech, jako jsou například polovodiče, tomu tak není. Materiály, ve kterých je elektrický odpor konstantní, se nazývají lineární nebo ohmické. Pro ně je charakteristika proudového napětí, tj. Funkce napětí jako funkce proudu U (I), lineární.

Ohmův zákon nelze považovat za základní přírodní zákon, protože je platný pouze pro určitou třídu materiálů, především kovů. Ovšem hraje důležitou roli ve fyzice a v každodenním životě, protože nám umožňuje jednoduše stanovit důležité fyzické veličiny v elektrickém obvodu. Zejména díky zákonu společnosti Ohm obvod DC vypočítá ztrátu elektrické energie při přenosu a spotřebě. Ohmův zákon se používá také pro výpočet požadované hodnoty odporu, která by měla být zahrnuta do elektrického obvodu tak, aby plnila své funkce s maximální účinností.

Závislost odporu na teplotě ohmických materiálů

Vzhledem k zákonům DC obvodů by mělo být uvedeno, jak se odpor mění se zvyšující se teplotou. Analogicky s elektrickou vodivostí materiálu ve fyzice se zavádí koncept specifického elektrického odporu ρ, který je spojen s odporem podle následujícího vzorce: R = l * ρ / A.

Bylo zjištěno empiricky, že u ohmických materiálů platí ρ následující teplotní závislost: ρ = ρ ₀ * [1 + α (TT ₀ ) + β (TT ₀ ) ² + ...], zde ρ ₀ je specifický odpor tohoto materiálu teplota T ₀ , která se často předpokládá jako 20 ° C.

U kovových materiálů v rozmezí od 0 do 200 ° C je rezistivita lineárně závislá na teplotě, tj. Ρ = ρ ₀ * [1 + α (TT ₀ )], kde α je koeficient teplotní odolnosti, což je pozitivní hodnota pro kovy, že elektrický odpor se zvyšuje lineárně s rostoucí teplotou pro kovy. Toto chování je spojeno s poklesem vzdálenosti, kterou elektron prochází mezi dvěma srážkami s ionty mřížky se stoupající teplotou.

Je zajímavé poznamenat, že v polovodičích se s rostoucí teplotou snižuje odpor. Tato skutečnost je spojena s nárůstem počtu nosičů elektrického proudu při ohřevu polovodičového materiálu, například křemíku nebo germania.

Kirchhoffovy zákony

Ve školách ve stupni 10 nejsou zákony stejnosměrného proudu omezen na zákon Ohm. Školní osnovy také zkoumají zákony Kirchhoff. Existují dva zákony Kirchhoff pro stejnosměrný proud. Jsou založeny na zákon o ochraně energie a nabíjení v elektrickém obvodu. Následující jsou formulace obou zákonů Kirchhoff:

1. Pro každý uzel elektrického obvodu se součet všech proudů vstupujících do tohoto uzlu rovná součtu proudů, které ho opouštějí. Tato formulace odráží zákon zachování náboje.
2. V každém obvodu s uzavřenou smyčkou se součet všech poklesů napětí na prvcích tohoto obvodu rovná napětí, které je dodáváno. Druhý zákon Kirchhoffa odráží zachování potenciální energie v elektrickém obvodu.

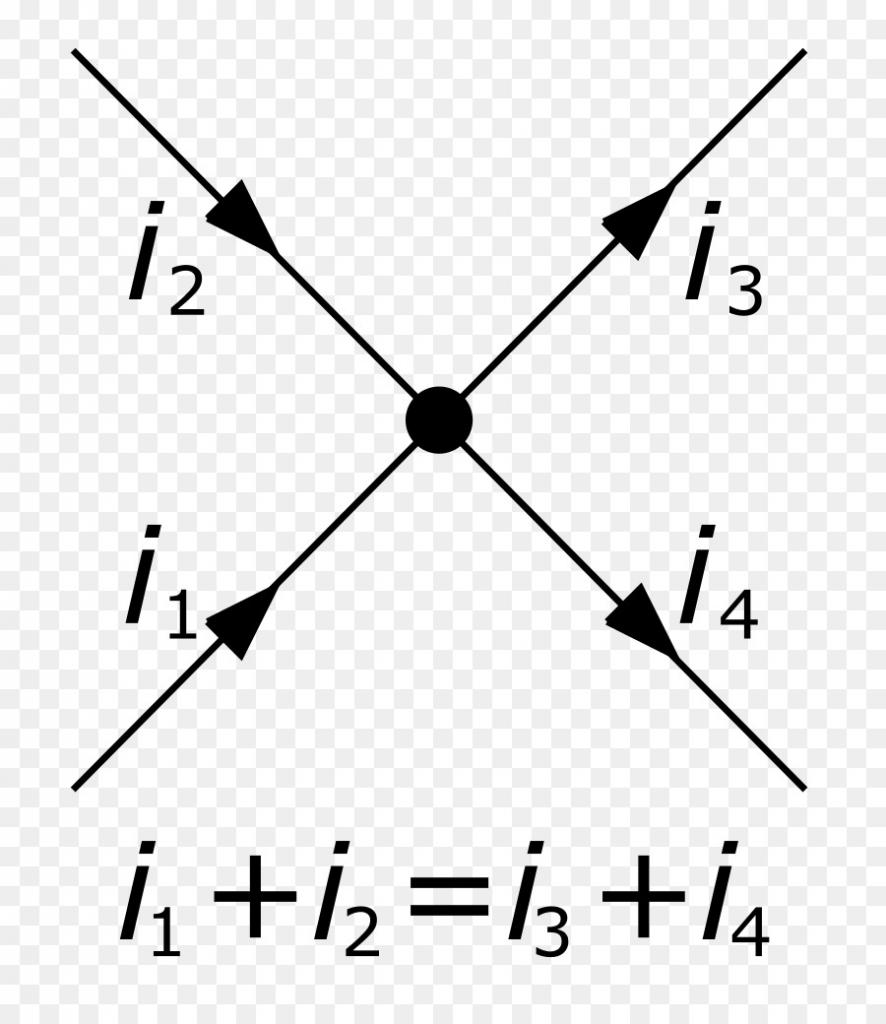
Tyto zákony byly poprvé zaznamenány v roce 1846. V současné době jsou široce používány v elektrotechnice a elektronice k určení neznámých proudů, napětí a odporů v obvodech. Všimněte si, že v případě přítomnosti nenulového elektrického odporu v obvodu R se část elektrické energie změní na teplo Q, které se nazývá Joule a vypočte se podle vzorce Q = I ² Rt, kde t je doba proudu protékající obvodovým prvkem s odporem R.

Praktická aplikace zákonů Ohmových a Kirchhoffových

Uvádíme příklad problému zákonů stejnosměrného proudu. Na následujícím obrázku je uveden příklad elektrického obvodu, který se skládá ze dvou obvodů, dvou zdrojů napětí a 5 rezistorů s různými odpory. Úkolem je najít neznámé proudy I _x a I _y . Okamžitě je třeba říci, že směr v obou obrysech je zvolen libovolně, v tomto případě ve směru hodinových ručiček.

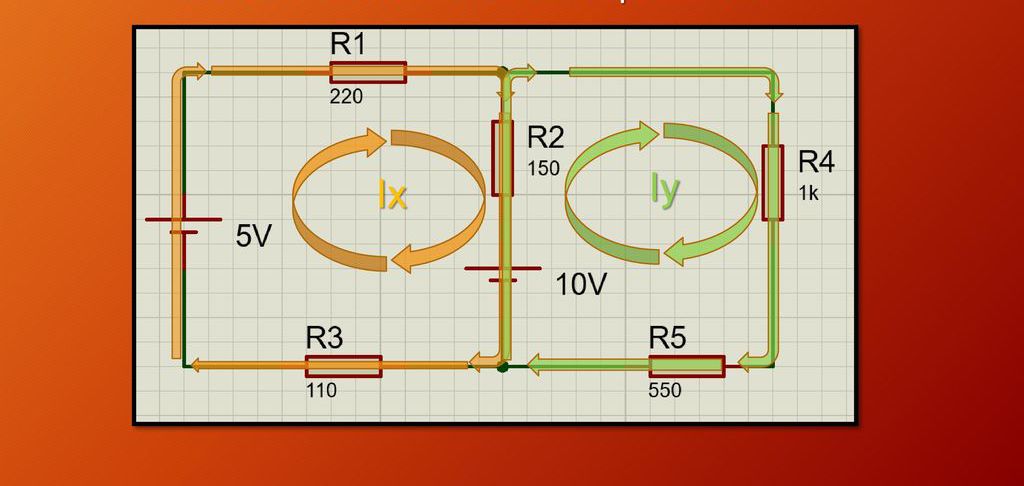
Dále musíte zvážit každý obvod zvlášť. Začněte věnovat pozornost obvodu s neznámým proudem I _x . Pro zvolený obvod je nutné aplikovat druhý zákon Kirchhoff, tedy zákon, který říká, že napětí poklesne napříč všemi odpory a napájecí napětí ze všech proudových zdrojů je stejné. Při použití tohoto zákona dostaneme: 5-10 = I _x * R ₁ + (I _x -I _y ) * R ₂ + I _x * R ₃ . Při sestavování tohoto výrazu byl vzat v úvahu znaménko zvoleného směru proudu I _x jako kladný směr, proto je potenciální rozdíl u zdroje 5 V kladný a při zdroji 10 V je záporný. Mějte také na paměti, že při uvážení tohoto obvodu je také nutné vzít v úvahu proud I _y, který proudí podle zadaných symbolů prostřednictvím rezistoru R ₂ .

Teď získáme podobnou rovnici pro druhý obvod s neznámým proudem I _y . Tento výraz bude mít formu: 10 = (I _y- I _x ) * R ₂ + I _y * R ₄ + I _y * R ₅ . Ve druhém okruhu je pouze jeden zdroj energie (10 V), a proto vstupuje pouze do výrazu odvozeného z 2. Kirchhoffova zákona.

Tak jsou získána dvě rovnice, ve kterých existují dvě neznámá: I _x a I _y . Zůstává kombinovat tyto výrazy do systému lineárních rovnic a vyřešit je. Níže uvedený obrázek ukazuje daný obvod a výsledný systém rovnic pro určení neznámých proudů.

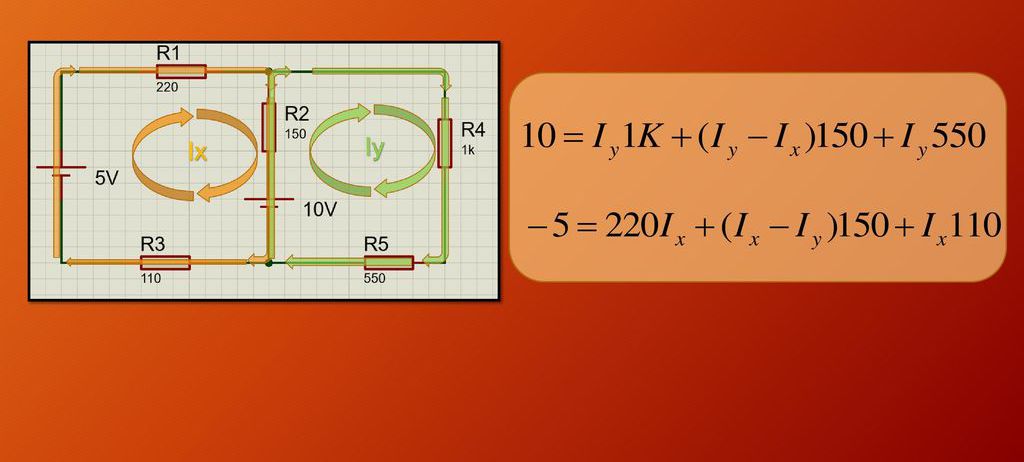
Řešení systému rovnic získáme tak, že I _x = -0.00882 A = -8.82 mA a I _y = 0.0051 A = 5.1 mA. Znaménko mínus znamená, že ve skutečnosti proud proudí ve směru, který je opačný k zvolenému. V důsledku toho protéká proudem 8,82 mA přes rezistory R1, R3 přes rezistory R ₄ , R ₅ - 5,1 mA a přes odpor R ₂ - I _y - I _x = 13,92 mA.