Korelační a regresní analýza: aplikace, hlavní fáze

Koncept korelační regresní analýzy předpokládá řadu operací, totiž určení blízkosti vztahu, jeho směru a vytvoření rovnice popisující podobu vztahu. Tento typ analýzy obsahuje dvě samostatné složky: korelační a regresní analýzu.

Hodnota a hlavní fáze procesu korelační a regresní analýzy ekonomických jevů

Korelace a regresní analýza jsou jedním ze způsobů řešení problémů a hledání informací. Umožňuje určit společný vliv mnoha vzájemně souvisejících a současně působících znaků, jakož i samostatný vliv každého atributu na ekonomický jev (proces). Díky tomuto typu analýzy je možné odhadnout míru vzájemného vztahu mezi několika charakteristikami, mezi charakteristikami a získaným výsledkem a také modelovat regresní rovnici popisující formu vzájemného vztahu.

Etapy analýzy

Korelační a regresní analýza ekonomických procesů je rozdělena do několika fází:

1. Definice argumentů a předběžné zpracování podmíněných informací.
2. Definice blízkosti a formy vzájemného vztahu mezi několika znaky.
3. Modelování prezentovaného ekonomického procesu a analýza výsledného modelu.
4. Uplatnění konečných výsledků ke zlepšení plánování a řízení modelu.

Homogenita statistické informace může být stanovena pomocí dvou technik. Nejprve je třeba stanovit a vyřadit hodnotu faktorů, které se od všech veličin výrazně liší. Poté se provede statistická studie o homogenitě provedením kontroly nezávislosti vzorku a jeho zařazení do jediné sady s normálním rozdělením.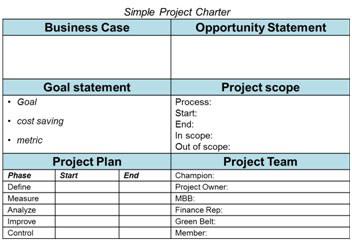

Regresní model je určen metodou nejmenších čtverců, která poskytuje nejlepší aproximaci odhadu výsledků, určeného regresní rovnicí, k jeho faktorům.

Korelace a regresní analýza: parametry vytvořeného modelu

Nejdůležitějšími faktory určujícími charakteristiky modelu se považují:

• Koeficienty dvojice korelace (demonstrují sílu vztahu dvou faktorů).
• Koeficient vícenásobné korelace (určuje vztah výsledku a faktorů).
• Koeficienty soukromého určení (ukazují vliv změny argumentu na změnu požadovaného znaku).
• Koeficient vícenásobného určení (ukazuje poměr všech argumentů na změnu požadované charakteristiky).
• Soukromé koeficienty elasticity (charakterizovat vliv faktorů na výsledek, vyjádřený v jediném měřítku v procentech).

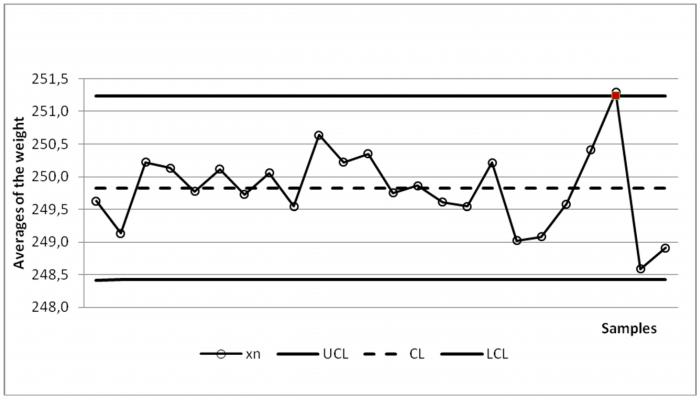
Účel analýzy

Hlavními úkoly analýzy korelační a regresní analýzy jsou identifikace faktorů, které významně ovlivňují hospodářský výsledek jevu nebo procesu a využití získaných informací pro zlepšení plánování ekonomického procesu nebo jevu.

Parametrické metody analýzy

Všechny výrobní procesy jsou úzce spjaty. Tento vztah je stochastický (výsledek závisí na mnoha faktorech) a funkční (výsledek se mění o stejné množství jako faktor). Stochastická závislost je často korelativní povahy, tj. Hodnota faktoru současně odpovídá několika hodnotám výsledku, které mají zcela odlišné směry.

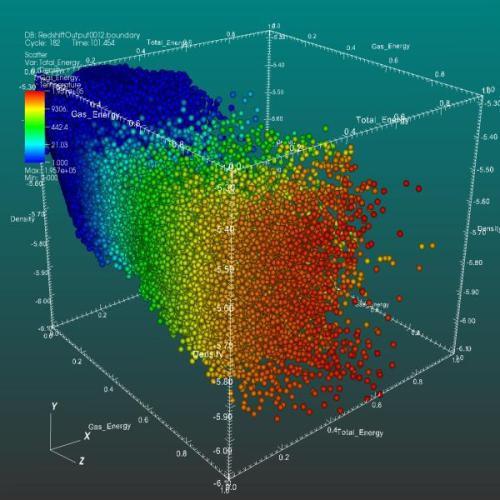
Korelační mřížka

Korelační vztah může mít jeden nebo více faktorů, má pozitivní nebo zápornou směrovost, je rovný nebo křivočarý (v závislosti na výrazu). Je možné určit, který typ vztahu se vztahuje pomocí korelační mřížky. Je postavena v pravoúhlých osách souřadnic.

Frekvence umístěné v blízkosti diagonálů naznačují vysokou korelaci znaků. Frekvence umístěné v blízkosti diagonálu procházejícího levým a pravým horním rohem ukazují pozitivní směr, zatímco ty, které procházejí levým horním a pravým dolním rohem, ukazují opačný směr. Frekvence umístěné ve tvaru oblouku naznačují křivočarý vztah a náhodně rozptýlené - o absenci vztahu vůbec.

Základní metoda korelační analýzy je lineární. korelační koeficient. Může to trvat od -1 do +1. Čím blíže je hodnota 1, tím silnější je vazba mezi faktorem a výsledkem. Pozitivní hodnoty naznačují přímý vztah a záporné hodnoty naznačují inverzní. Koeficient má hodnotu "nula", pokud neexistuje žádný vztah mezi značkami.

Neparametrické metody analýzy

Řada metod umožňuje vyhodnotit vztah jevů bez kvantitativního vyjádření vlastností a podle toho i distribučních parametrů. Jsou nazývány neparametrické. Mezi ně patří:

• Kendallův korelační koeficient (určuje vztah kvantitativních a kvalitativních hodnot ukazatelů, pokud jsou předmětem hodnocení).
• Spearmanův korelační koeficient (přiděluje pozice každému argumentu a výsledku, na základě kterého jsou určeny rozdíly a je vypočten indikátor).
• Korelační koeficient Fechnerových znaků (určuje počet shody a nesouladů mezi odchylkami argumentů a výsledky jejich střední hodnoty).
• Další důležitou metodou korelační a regresní analýzy je metoda nejmenších čtverců, která umožňuje určit analytický výraz vztahů výsledného znaku a jeho faktoru. Spočívá v budování systému rovnic a určování parametrů těchto rovnic.

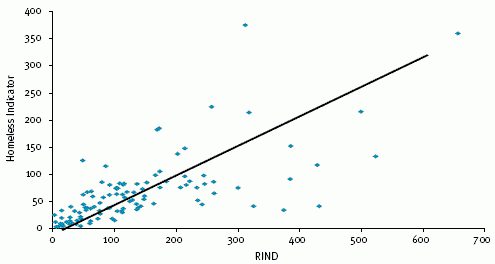
Korelace a regresní analýza: příklad

V statistice a ekonomice se používá široká škála typů a objektů analýzy. Statistické metody analýzy jsou zaměřeny na studium opakovaných procesů, aby bylo možné dlouhodobě předpovídat chování ekonomických jevů.

Například pro analýzu socioekonomického vývoje území je nutné studovat ukazatele životní úrovně obyvatelstva. Korelační a regresní analýza ve statistikách vám umožňuje vytvářet regresní rovnice a určit korelační koeficienty, které ukazují vztah mezi životní úrovní a rozvojem území. Životní úroveň je určena příjmem a hlavním zdrojem příjmu je plat. V tomto případě činí faktor mzda a výsledek je obyvatelstvo s nízkými příjmy.

Analýza software

Pro usnadnění výpočtů můžete provést korelační analýzu v aplikaci Excel. V tomto programu existuje řada nástrojů, které usnadňují výpočty. Mezi nimi funkce "Korelace", která umožňuje vytvořit matici koeficientů a různých parametrů. Je znázorněna ve formě tabulky. Korelační koeficienty se používají jako sloupce a řádky. Na základě údajů získaných v tabulce bude nutné provést korelační analýzu. Příklad sekvence analýzy:

1. V příkazu "Service" vyberte možnost "Analýza dat".
2. Jako nástroj pro analýzu vyberte položku "Korelace".
3. V okně, které se zobrazí, v řádku "Vstupní interval" zadejte rozsah analyzovaných dat, vyberte položku "Seskupování" v řádku "Výstupní parametry", zadejte výstupní rozsah výsledků a klepněte na tlačítko "OK".

Výsledkem je korelační matice umístěná ve výstupním rozsahu. Uvnitř bude indikován lineární korelační koeficient, který posuzuje těsnost a podobu vztahu mezi indikátory.

Analýza v aplikaci Excel

V aplikaci MS Excel se pro korelační a regresní analýzu používá funkce "Korelace". Příklad výpočtu koeficientů bude zvažován později. Tato funkce tvoří matici s koeficienty blízkosti vztahu mezi různými parametry. V důsledku toho se vytvoří čtvercový tabulka obsahující korelační koeficienty na průsečíku řádků a sloupců.

Pro analýzu bude třeba provést řadu konkrétních akcí:

1. Otevřete příkaz "Service" a v něm položku "Data Analysis".
2. V okně, které se zobrazí, zadejte položku "Korelace" v seznamu "Nástroje pro analýzu".
3. V okně "Korelace", které se otevře, zadejte vstupní interval jako rozsah buněk obsahujících analyzované informace (měl by být alespoň dva sloupce), zaškrtněte volbu "Seskupování" av poli Výstupní parametry vyberte levou horní buňku, kde korelační matice.
4. Klepněte na tlačítko OK.

V důsledku výpočtů se zobrazí čtvercový tabulka s korelačními koeficienty.

Regresní analýza v MS Excel

Pro výpočet lineární rovnice Regrese popisující vztah mezi faktory a výsledkem, v MS Excel se používá "Linean" statistická funkce. Chcete-li jej používat, musíte:

1. Vyberte prázdnou oblast, ve které budou zobrazeny výsledky analýzy.
2. Otevřete "Master of Functions", najděte kategorii "Statistical" a v něm funkci "Lineine" a klikněte na OK.
3. Do pole "Známé hodnoty y " zadejte rozsah analyzovaných výsledků v poli "Známé hodnoty x" - rozsah analyzovaných faktorů.
4. Pole "Konstantní" označuje přítomnost volného termínu v rovnici (1 - ano, 0 - ne) av poli "Statistika" - potřeba zobrazit další informace (1 - zobrazí se další informace, 0 - zobrazí se pouze odhady parametrů). Ve výchozím nastavení můžete v obou polích specifikovat 1.
5. Klepněte na tlačítko OK.

V horní části dříve vybrané oblasti se zobrazí počáteční prvek tabulky. Chcete-li zobrazit všechna data, musíte stisknout klávesu F2 a současně kombinaci kláves Ctrl + Shift + Enter.

V důsledku toho se regresní informace zobrazí jako tabulka se dvěma sloupci a pěti řádky:

Výsledky by měly být nahrazeny rovnicí lineární regrese, která vypadá takto: y = a + bx. Hodnota z buňky v průsečíku řádku 1 a sloupce 2 nahrazuje koeficient a. Hodnota v průsečíku řádku 1 a sloupce 1 se používá jako koeficient b.

Koeficient určení udává, jaká část výsledku je vysvětlena pomocí studovaného faktoru. Zbývající část výsledků je určena faktory, které jsou v lineárním modelu nezohledněny.