Rozložení čtvercových trinomiálů do faktorů: příklady a vzorce

Rozložení čtvercových trimestrů na faktory se týká úkolů školy, kterým se dříve či později čelí všichni. Jak to udělat? Jaký je vzorec pro rozklad čtvercových trinomálních faktorů? Postupně budeme chápat příklady.

Obecný vzorec

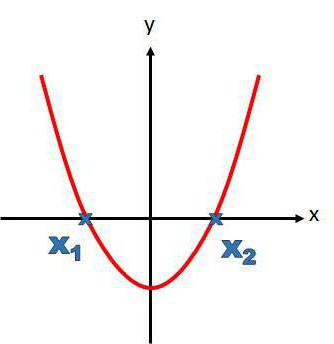
Rozklad čtvernových trinomiálů do faktorů se provádí řešením kvadratické rovnice. Jedná se o jednoduchý úkol, který lze vyřešit několika způsoby - nalezení diskriminujícího, pomocí věty Viety existuje také grafické řešení. První dvě metody jsou studovány na střední škole.

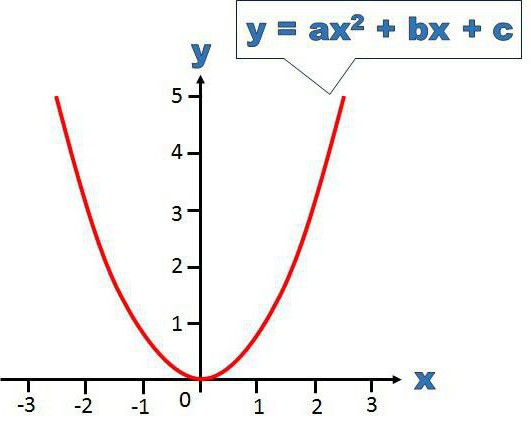
lx ² +kx+n=l(xx ₁ )(xx ₂ ) (1) Obecný vzorec je následující: lx ² + kx + n = 1 (xx ₁ ) (xx ₂ ) (1)

Algoritmus provádění úkolů

Abyste provedli faktorizaci čtvercových trinomiálů, musíte znát větu Vit, mít řešení po ruce, najít řešení graficky nebo hledat kořeny rovnice druhého stupně prostřednictvím diskriminačního vzorce. Je-li udán čtvercový trinom a musí být faktorizován, postupnost kroků je následující:

1) Rovná se původní rovnice na nulu, aby se získala rovnice.

2) Přineste takové termíny (pokud je taková potřeba).

3) Najděte kořeny jakýmkoli známým způsobem. Grafická metoda se nejlépe použije, pokud je předem známo, že kořeny jsou celé čísla a malé čísla. Je třeba mít na paměti, že počet kořenů se rovná maximálnímu stupni rovnice, kvadratická rovnice dva kořeny.

4) Nahraďte hodnotu x ve výrazu (1).

5) Zaznamenejte rozklad čtvercových trinomálních faktorů.

Příklady

Nakonec pochopte, jak je tento úkol vykonáván, umožňuje praktické cvičení. Ilustru faktoringu čtvercových příkladů:

Je třeba rozšířit výraz:

x ² -17x = -32

Zaměřme se na náš algoritmus:

1) x ² -17x + 32 = 0

2) podobné pojmy jsou sníženy

3) podle vzorce Viet, je obtížné najít kořeny pro tento příklad, protože je lepší použít výraz pro diskriminační:

D = 289-128 = 161 = (12,69) ²

x ₁ = 2,155

x ₂ = 14,845

4) Náhradu kořenů, které jsme nalezli v základním vzorci pro rozklad:

(x-2.155) _* (x-14.845)

5) Odpověď bude:

x ² -17x + 32 = (x-2.155) (x-14.845)

Zkontrolujte, zda řešení nalezená diskriminujícím odpovídají vzorce Viet:

2,155 + 14,845 = 17

14,845 ^. 2,155 = 32

Pro tyto kořeny je použita Vietova věta, byla nalezena správně, což znamená, že faktorizace, kterou jsme získali, je také správná.

Podobně rozloží 12x ² + 7x-6.

12x ² + 7x-6 = 0

D = 337

x ₁ = -7 + (337) ^1/2

x ₂ = -7- (337) ^1/2

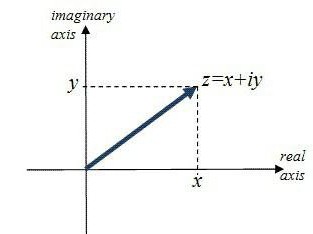
V předchozím případě byla řešení necelová, ale skutečná čísla, která se snadno nacházejí, mají kalkulačku před vámi. Nyní zvažte komplexnější příklad, ve kterém budou kořeny složité: factoring x ² + 4x + 9. Podle vzorce pro Vieta nelze najít kořeny a diskriminující je negativní. Kořeny budou v komplexní rovině.

D = -20

Vycházíme z těchto zajímavých kořenů -4 + 2i * 5 ^1/2 a -4-2i _* 5 ^1/2 , protože (-20) ^1/2 = 2i * 5 ^1/2 .

Získáme požadovaný rozklad, nahrazením kořenů obecným vzorcem.

Jiný příklad: musíte vyčíslit výraz 23x ² -14x + 7.

=0 Máme rovnici 23x 2 -14x + 7 = 0

D = -448

To znamená, že kořeny jsou 14 + 21,166i a 14-21,166i. Odpověď bude:

23x 2 -14x + 7 = 23 (x-14-21,166i) * (x-14 + 21,166i).

Uveďme příklad, který lze vyřešit bez pomoci diskriminující osoby.

Předpokládejme, že potřebujete rozšířit kvadratickou rovnici x 2 -32x + 255. Je zřejmé, že to může být vyřešeno diskriminujícím, ale v tomto případě je rychlejší zvednout kořeny.

x 1 = 15

x 2 = 17

Takže x 2 -32x + 255 = (x-15) (x-17).