Příklad algoritmu Diffie Hellman

Zveřejnění tématu kryptografie s veřejným klíčem musí začínat historickou cestou problému. Whitfield Diffie a Martin Hellman se poprvé zeptali na otevřenou metodu předávání klíčů. Stalo se to v roce 1976. Publikace provedla první pokusy o řešení tohoto problému. Jejich řešení nebylo bez chyb, ale položilo základy pro zcela jiný způsob myšlení v oblasti šifrovaného přenosu dat.

Předpoklady pro vytvoření algoritmu Diffie-Hellman

Až do tohoto bodu bylo ověřování a šifrování možné pouze prostřednictvím sdíleného tajného klíče. S rozvojem technologií se problém stal nejsilnějším. Pokud je třeba 10 osob mezi sebou přenést data přes nejisté kanály, budou si muset navzájem vyměňovat hesla. Tento úkol vypadá docela reálný. Dokonce je potřeba je aktualizovat. Koneckonců, pro 10 přátel budete potřebovat pouze 45 tajných klíčů. A pokud budou kontakty 100? Vyžaduje to 4950 hesel. Situace se rozrůstá jako sněhová koule.

Hlavním úspěchem Diffie a Hellmanu byla správná formulace otázky a důvtipná odpověď na ni. Navrhovaly, že data mohou být šifrována jedním způsobem a dešifrována v jiném. To znamená, že máte 2 klíče. Ten, který se používá pro šifrování, může zůstat otevřený. Každá osoba tedy může zašifrovat zprávu, ale pouze majitelé druhého tajného klíče ji mohou dešifrovat. Ale jak implementovat algoritmus pro přenos takového klíče? Vědci byli částečně schopni odpovědět.

Krátká matematika: skupiny

Diffie-Hellmanův algoritmus nebo protokol (dále DH) pracuje s pomocí primárních čísel. Nechť je dostatečně velké číslo, které patří k souboru primární čísla. Tento algoritmus zahrnuje použití počtu 250 až 500 bajtů. Nechť Za je multiplikativní skupina reziduálního kroužku modulo a, který bude použit v šifrovacím algoritmu Diffie-Hellman. Skládá se z množiny čísel 1, ..., a-1.

Vezměte nějaký prvek b ze skupiny Z a považujte nekonečnou sekvenci 1, b, b ² , b ³ , b ⁴ , ... Ze skutečnosti, že skupina Z _{a je} definice konečnou množinou, dříve nebo později zvažovaná sekvence {b} začne opakovat. Nastavte b ⁱ = b ^j (i <j).

Nyní rozdělíme každou část rovnosti na b ⁱ (modulo a) a dostaneme b ^ji = 1. To znamená, že existuje číslo k = ji, pro které platí b ^k = 1 (mod a). Nejmenší k, pro kterou platí tato rovnost, se nazývá pořadí b. Aby nedošlo k záměně s jinou speciální literaturou, standardní matematické notace se používá k vysvětlení systému Diffie-Hellman.

Zvyšování počtu b, nazývaného generujícím prvkem, k síle, získáme sekvenci čísel (set) 1, ..., b ^k-1 . Počet prvků v této sadě je přesně k.

Multiplikační vlastnost modulo a říká, že existuje alespoň jedno číslo b generující všechny prvky skupiny Z * _a . Jinými slovy, existuje číslo, pro které platí k = a - 1. Tato vlastnost nám dovoluje reprezentovat čísla skupiny Z * _a ve tvaru 1, b, b ² , ... b ^a-2 . Takové číslo b se nazývá primitivní číslo skupiny.

V pokračování je snadné dokázat ze skupiny, že množina generovaná číslem b je také samotná skupina a dědí všechny vlastnosti skupin. Jinými slovy, operace uvnitř vytvořené skupiny nebo podskupiny mohou být prováděny přesně stejným způsobem jako ve skupině modulo a.

Zvažte prohlášení. Pro každý prvek b je jeho pořadí dělitel a-1. Je snadné ji ukázat. Nechte a = 7. Číslo b = 3 je primitivní, protože 1, ..., b ⁵ = 1, 3, 2, 6, 4, 5. Pak číslo h = 2 vytvoří podskupinu 1, ..., h ² = 1 , 2, 4, protože h ³ = 2 ³ mod 7 = 1. h = 6 generuje podskupinu 1, 6. Velikost skupin je 3 a 2, resp. Je zřejmé, že jsou dělitelé čísla a-1 = 6.

První algoritmus DH

V původní verzi fungoval algoritmus následovně. Velké množství a je vybráno ze sady jednoduchých a primitivních prvků b generujících Z * _a . Obě čísla a a b představují veřejný klíč, jsou známy všem, včetně útočníků. Jak tedy skrýt zprávy?

V tomto kroku se Diffie a Hellman objevili s velkým geniálním krokem. Předpokládejme, že máme dva lidi, kteří vzájemně komunikují: A a B. Nejprve si A vybírá náhodné číslo x od Z * _a , což odpovídá volbě čísla z {1, ..., a-1}. Potom vypočítá hodnotu pomocí vzorce (b ^x mod a) a odešle jej B. Na druhé straně B volí určitý počet y z téže sady, vypočítá hodnotu (b ^y mod a) a odešle výsledek zpět do A.

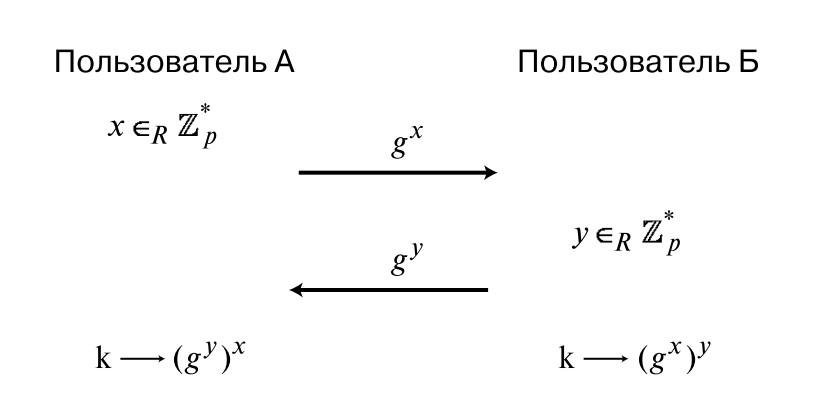
V tak choulostivém způsobu se ukázalo, že tajný klíč vypadá jako b ^xy . Vzhledem k vlastnostem stupňů, který říká g ^xy = (g ^y ) ^x , může interlocutor A vypočítat požadovanou hodnotu a rozluštit informace, které mu byly zaslány. Stejným způsobem je tato hodnota vypočtena účastníkem B. Tak mají oba stejné tajné klíčové hodnoty.

Jaké jsou problémy s vetřelcem při této výměně informací? Může zachytit čísla g ^x a g ^y . A dokonce i s vědomím veřejných klíče není problém výpočtu g ^xy triviální, t. Protože neexistuje žádný účinný algoritmus pro nalezení požadované hodnoty v distribuci klíčů Diffie-Hellman. Tento problém je známý jako problém výpočtu diskrétního logaritmu.

Mediátorský útok

Jednou ze slabostí primárního algoritmu Diffie-Hellman je jeho zranitelnost vůči zprostředkovaným útokům. Co to znamená? Interlocutor A ví, že komunikuje s určitou tváří, ale konkrétně s kým - nemá tušení. Útočník tedy může proniknout do přenosu informací a napodobovat účastníka B při komunikaci s A a naopak. Nikdo z nich nebude mít podezření, že se něco děje.

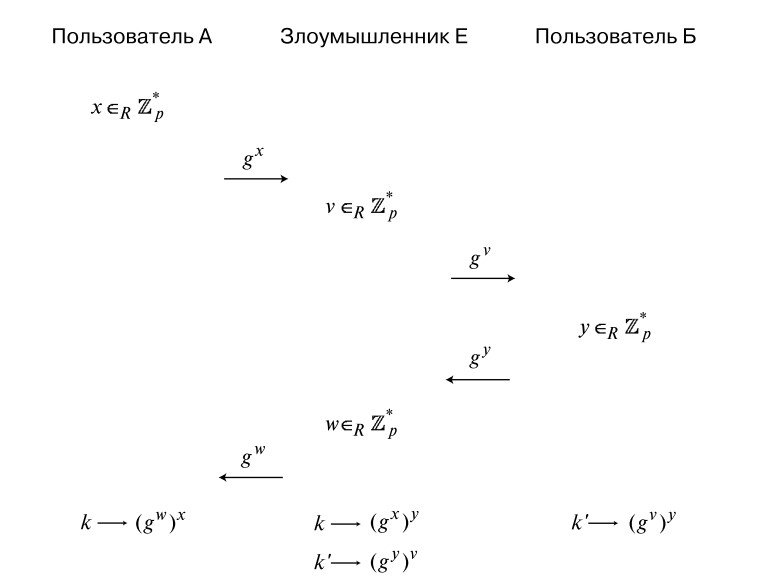
Existuje pouze jedna oblast použití, ve které jsou vyloučeny útoky na algoritmus Diffie-Hellman. Jedná se o telefonický a videohovor. Zde se mohou účastníci vzájemně poznat, takže mediátor nebude moci proniknout.

Úskalí

Kromě útoku zprostředkovatele protokol DH obsahuje řadu dalších problémů. Jednou z nevýhod je například situace, kdy primitivum není primitivní. Pak generuje pouze podskupinu. Vzhledem k zúžení počtu možných možností útočník otevírá možnost jejich vyhledávání.

Problémy způsobené tímto nedostatkem lze předejít, pokud každý z účastníků kontroluje správnost čísel a a b před zahájením výměny dat. To znamená, že a je primární číslo a b je primitivní. Nicméně pokud jde o zabezpečení prostřednictvím implementace určitých jednotných, nepovinných kroků, uživatelé je často ignorují.

Další závažný problém vzniká na základě podskupin modulo a. Pokud se útočník rozhodne změnit g ^x na 1, aby mu usnadnil odposlouchávání, uživatelé ho mohou snadno zjistit tak, že zkontroluje číslo pro zápas. Pokud však klíč vymění za nízké číslo objednávky, uživatelé nebudou moci nic podezřívat. A protože počet prvků v sadě s nízkým pořadím bude malý, bude útočník muset vyřešit malý počet možností pro dekódování.

Spolehlivost prvočísel

DH algoritmus používá velký a spolehlivý počet mnoha jednoduchých. Jak přesně to zvolit? Analyzujeme kroky.

1. Pomocí vzorce a = 2k + 1 zvolte čísla a a k tak, aby byly jednoduché.
2. Ze sady 1, ..., a-1 vylučujeme 1 a a-1.
3. Vezměte náhodné číslo x z množiny zbývající po druhém kroku a najděte hodnotu b = x ² (mod a).
4. Ujistěte se, že b není rovno 1 nebo a-1. Pokud se b rovná jedné z zakázaných hodnot, měli byste zvolit další x. A opakujte operaci.

Takto získaná množina (a, k, b) může být považována za dostatečnou pro použití v algoritmu výměny klíčů Diffie-Hellman. V souladu s tím musí příjemce zprávy také zkontrolovat hodnotu, která musí být síla b, a ujistit (například funkce symbolu Legendre), že spadá do množiny generované číslem b.

Používání podskupin

Hlavní nevýhodou výše uvedeného algoritmu je nedostatečná efektivita. Za předpokladu, že délka primárního čísla a je n bitů, pak k je n-1 bitů. Ukazuje se, že všechny stupně budou n-1 dlouhé. Pak operace exponentiace v průměru bude sestávat ze 3n / 2 násobení mod a. To je docela velký proces.

Abychom tento problém zvládli, bylo rozhodnuto použít menší podskupiny. Jaký je výkon v tomto případě? Pokud se číslo a skládá z 2000 bitů, pak je pro výpočet b ^x nutné 3000 násobných operací. Pomocí podskupin lze toto číslo snížit na ~ 400. Toto významné zvýšení efektivity algoritmu umožňuje jeho plné uplatnění. Například algoritmus Diffie-Hellman se třemi nebo více členy.

Co by mělo být délka a

Správný výběr velikostí parametrů algoritmu Diffie-Hellman je poměrně složitý úkol. Společným požadavkem ve světě kryptografie je například podmínka, že útočník potřebuje nejméně 2 ¹²⁸ kroků k proniknutí do systému. Je-li v symetrickém šifrovacím algoritmu vyhovovat takový požadavek, je to snadné, v algoritmech s veřejným klíčem je to skutečný problém. Pokud splníte výše uvedený požadavek, délka a musí obsahovat alespoň 850 bajtů.

V praxi tato velikost vytváří v systému velké problémy s výkonem, protože operace s veřejným klíčem trvají mnohem déle, než je například symetrické šifrování se 128 nebo 256 bitovými klávesami. Tak jak to být? Minimální délka veřejného klíče musí začínat na 2048 bitů. Přestože čím delší je klíč, tím vyšší je úroveň zabezpečení. Zvažuje se především výkon systému a jeho náklady. Pokud vám to dovolí použít klíč 4096 bitů, musíte to udělat.

Jak se hodnotí požadovaná úroveň zabezpečení?

Rozměry klíče v symetrickém šifrování zůstávají nezměněny (128, 256 bitů) po celou dobu životnosti systému, zatímco velikosti veřejného klíče jsou vždy variabilní hodnotou. Pokud musíte vyvinout systém, který musí být používán po dobu 30 let a uchovávat údaje tajné po dobu nejméně 20 let poté, co byl systém vyřazen z provozu, musí být velikost symetrického šifrovacího klíče zpočátku dostatečně velká, aby chránila systém v příštích 50 letech.

Z důvodu zjevných problémů s výkonem, vzhledem k tomu, že algoritmus Diffie-Hellman šifruje mnohem větší počet operací, se požadavky na veřejné klíče liší. Platí po dobu jednoho roku a chrání data pro příštích 20 let, tj. Celkem 21 let. Vzhledem ke své variabilní velikosti může být klíč každým rokem vyměňován a vytvářet stále delší dobu, aby byla zajištěna požadovaná úroveň zabezpečení.

Nejlepší odhady například ukazují, že klíč s délkou 256 bytů je schopen zajistit ochranu dat po dobu ~ 20 let, délka 384 bajtů je 35 let a délka 512 bajtů činí 47 let atd. Počet je 6800 bitů, což zajišťuje, že útočník Pro jeho crack je vyžadováno 2 ¹²⁸ kroků, odvozených z podobných odhadů. Je to však pouze prognóza, kterou musíte důkladně důvěřovat. Můžete určit přesně předvídat vývoj událostí na 10 let dopředu, ale na 50 let - to je fantastické.

Praktické doporučení

Zde je několik praktických tipů, jak používat protokol DH. Zvolte k jako primární číslo 256 bitů. To je minimum, které může poskytnout přinejmenším dostatečnou úroveň zabezpečení proti útokům. Pro číslo a vyberte číslo, které by mělo tvar Na + 1, kde N je celé číslo. O velikosti čísla a byla uvedena dříve. Následně je vybráno a zkontrolováno náhodné číslo b pro několik podmínek. Za prvé, nemůže to být jednotka. Za druhé, b ^k = 1.

Na druhé straně by měl být každý účastník komunikace přesvědčen o následujících skutečnostech:

• a a k jsou primární čísla, délka k je 256 bitů, délka p je poměrně velká.
• číslo k je dělitel a-1.
• b není rovno 1 a b ^k = 1.

Tyto podmínky by měly být kontrolovány i bezpodmínečnou důvěrou ve zdroj.

Závěr

DH algoritmus je geniální řešení jednoho z vážných problémů a je stále aktivně používán v upravené podobě pro moderní bezpečnostní požadavky v různých protokolech. Například algoritmus Diffie-Hellman se používá v některých částech implementace protokolu IKE. Jeho použití by však mělo být metodické a opatrné kvůli přítomnosti zřejmých problémů a vážných nástrah.