Distribuční zákon násobení s ohledem na přidání

Matematici jsou líní lidé, takže vždy vytvořili nějaké vzorce, zákony, názvy. Jejich úsilí nebylo marné, nyní může moderní člověk snadno vyřešit rovnice a problémy. Je snadné dokázat teorémy o geometrii a to vše díky vzorcům, notaci, vlastnostem!

Zákony násobení a doplnění

Jsou určeny pro násobení a přidání čísel pouze tří. Jsou velmi užitečné, díky nim můžete snadno vyřešit velké rovnice. Každý z nich má svůj vlastní vzorec a jméno.

První zákon násobení a doplnění je kombinovaný zákon. Čísla jsou potom seskupena, protože vědí, že součet a produkt se stejně nezmění.

Druhý zákon násobení a přidání je peremeshitelny. V tomto případě se čísla přesouvají tak, jak to bude vhodné, protože vědí, že součet a produkt zůstanou stejné.

Třetí, nejčastěji používaný distribuční zákon. Jeho smyslem je provádět akce, které nejsou pro každé číslo zvlášť, ale okamžitě se vynásobte součtem. Naopak, přidáním faktoru do závorek se vynásobí každý pojem. Je to opravdu výhodné a stojí za to se naučit, jak používat tento zákon!

Tyto zákony nelze použít pro rozdělení a odečtení, protože mohou změnit konečný výsledek.

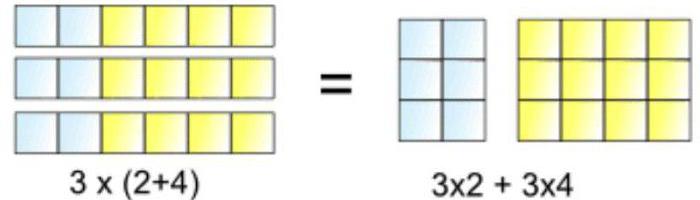
Distribuční právo

Je to velmi pohodlné, protože s jeho pomocí můžete vynásobit číslo bez jakýchkoliv potíží! A to vše proto, že je mnohem snazší distribuovat než jen znásobit každý faktor.

Z důvodu srozumitelnosti můžeme uvažovat například o tom, kde se používá pro násobení a doplnění.

Při daném výrazu: 3 x 2 + 3 x 5.

Toto je obvyklý výraz. Použijeme-li distribuční zákon, bude vypadat takto: 3 x (2 + 3) = 3 x 5 = 15.

Jak můžete vidět, pomocí tohoto pohodlného "nástroje", můžete vyřešit různé rovnice mnohem rychleji!

Vše ve světě má své vlastní jméno a znění, distribuční právo není výjimkou! Stojí za to zapamatovat si jeho znění, takže jej lze snadno použít za jakýchkoliv podmínek a za jakýchkoli okolností. Stojí za to pochopit její akce!

Příklad, kdy se vztahuje distribuční zákon násobení s ohledem na přidání

Zvažte další příklad, kdy platí tento zákon: 2 x 5 + 2 x 3 = 16.

Takový výraz byl původně a pak se stal: 2 x (5 + 3) = 2 x 8 = 16.

Jak můžete vidět, odpověď se nezměnila a bylo mnohem snazší provést akce! To je krásné! Mohli bychom náš život usnadnit!

Distribuční zákon násobení s ohledem na přidání je velmi užitečný, takže je třeba používat! Nebojte se vyzkoušet něco nového! Všechny vlastnosti, věty a vzorce jsou z matematiky z dobrého důvodu!