Příklady, jak vypočítat plochu válce

Existuje mnoho úkolů týkajících se válce. Musí najít poloměr a výšku těla nebo typ jeho průřezu. Navíc někdy musíte vypočítat plochu válce a jeho objem.

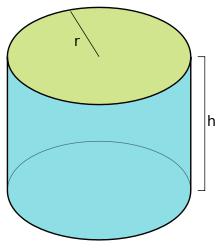
Které tělo je válec?

V průběhu školního vzdělávacího programu je studován kruhový tvar, tzn. Že je na základně válce. Ale je tu také eliptický pohled na toto číslo. Z názvu je zřejmé, že jeho základna bude elipsa nebo ovál.

Existují dvě základny válců. Jsou rovnocenné a jsou spojeny segmenty, které kombinují odpovídající body základen. Jsou nazývány generátory válců. Všechny generátory jsou rovnoběžné a rovnocenné. Představují boční povrch těla.

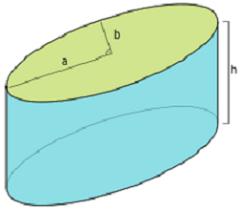
Obecně platí, že válec je nakloněné tělo. Pokud generátory tvoří základ s pravým úhlem, pak již hovoří o přímočaré osobě.

Je zajímavé, že kruhový válec je rotující těleso. Získává se otočením obdélníku kolem jedné ze stran.

Hlavní prvky válce

Hlavní prvky válce jsou následující.

1. Výška Je to nejkratší vzdálenost mezi základnami válce. Je-li rovný, výška se shoduje s generátorem.
2. Poloměr Coincides s tím, který může být držen u základny.
3. Osa. Jedná se o přímku, která obsahuje středy obou základen. Osa je vždy rovnoběžná se všemi generátory. V přímém válci je kolmý k základnám.
4. Axiální část. Vzniká v průsečíku válce rovinou obsahující osou.
5. Tečna roviny. Prochází jedním z generátorů a je kolmá na axiální část, která je vedena tímto generátorem.

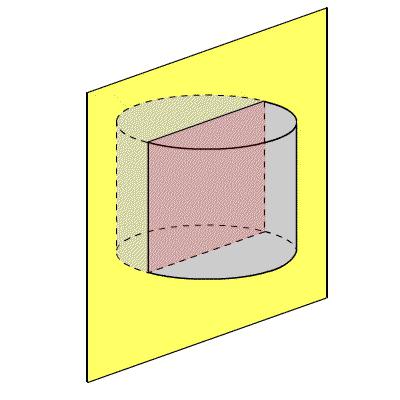
Jak je válec spojen s hranolem, který je do něj zapsán nebo je popsán v jeho blízkosti?

Někdy existují úkoly, při kterých je třeba vypočítat plochu válce, zatímco některé prvky prismu jsou známy. Jak se tyto údaje týkají?

Pokud je hranol zapsán do válce, pak jeho základny jsou stejné polygony. A jsou zapsány do příslušné základny válce. Boční hrany hranolu se shodují s generátory.

Na popsaném hranolu v podstavcích jsou pravidelné polygony. Jsou popsány kolem kruhů válečku, které jsou jejími základy. Letouny, které obsahují tváře hranolu, se dotýkají válce podél generátorů.

Na ploše boční plochy a základny pro přímý kruhový válec

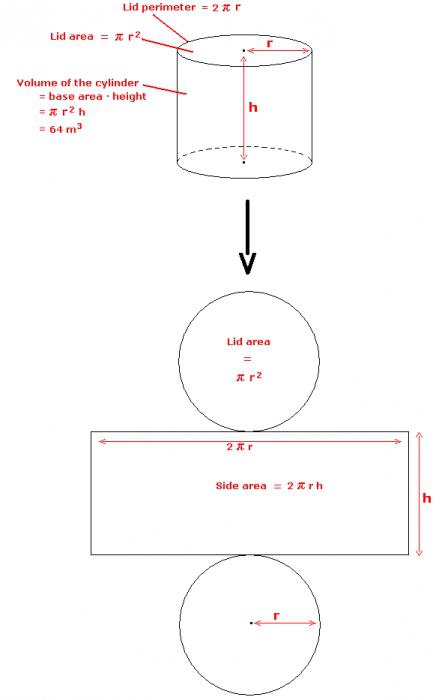
Pokud skenujete boční plochu, získáte obdélník. Jeho strany se shodují s generátorem a obvod důvody. Boční oblast válce se tedy bude rovnat výsledku těchto dvou veličin. Pokud napíšete vzorec, získáte následující:

S _strana = l * n,

kde n je generátor, l je délka kruhu.

A poslední parametr se vypočítá podle vzorce:

l = 2 π * r,

zde r je poloměr kruhu, π je číslo "pi", které se rovná 3,14.

Vzhledem k tomu, že základna je kružnice, její plocha se vypočítá pomocí následujícího výrazu:

S _primární = π * r ² .

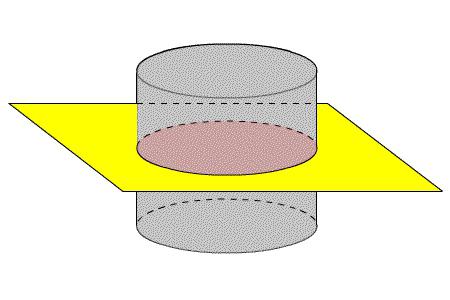
Na ploše celého povrchu přímého kruhového válce

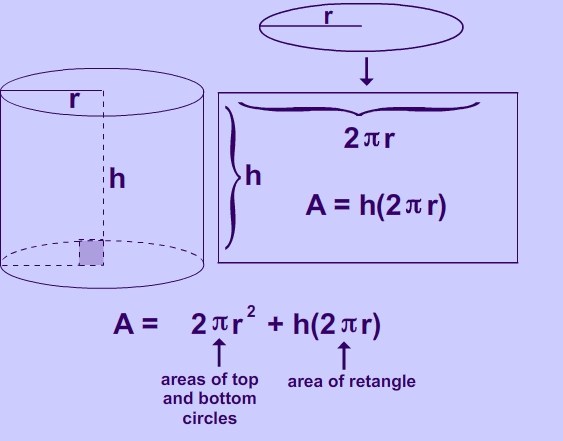
Vzhledem k tomu, že je tvořena dvěma základnami a bočním povrchem, je třeba tyto tři množství přidat. To znamená, že celková plocha válce bude vypočtena podle vzorce:

S _podlaha = 2 π * r * n + 2 π * r ² .

Často je napsána v jiné podobě:

S _podlaha = 2 π * r (n + r).

Na plochách nakloněného kruhového válce

Pokud jde o důvody, pak jsou všechny vzorce stejné, protože jsou stále kruhy. Ale boční plocha nedává obdélník.

Pro výpočet bočního povrchu šikmého válce bude nutné vynásobit hodnoty generátoru a obvod průřezu, který bude kolmý na zvolený generátor.

Vzorec vypadá takto:

S _strana = x * P,

kde x - délka válce generátoru, P - obvod úseku.

Část mimochodem je lepší zvolit tak, aby vytvořila elipsu. Potom budou výpočty jeho obvodu zjednodušeny. Délka elipsy se vypočítá podle vzorce, které dává přibližnou odpověď. Ale často to stačí pro školní úkoly:

l = π * (a + c),

kde "a" a "b" jsou poliaxy elipsy, tj. vzdálenost od středu k nejbližšímu a nejvzdálenějšímu bodu.

Plocha celého povrchu se musí vypočítat podle následujícího výrazu:

S _podlaha = 2 π * r ² + x * R.

Jaké jsou některé části přímého kruhového válce?

Když část prochází osou, je její oblast definována jako produkt generátoru a průměr základny. To je způsobeno skutečností, že má tvar obdélníku, jehož strany se shodují s uvedenými prvky.

Abychom našli plochu průřezu válce, která je rovnoběžná s axiálním válcem, potřebujeme také vzorec pro obdélník. V této situaci se jedna strana stále shoduje s výškou a druhá se rovná akordu základny. Druhý se shoduje s čárou čáry podél základny.

Když je úsek kolmý k ose, má tvar kruhu. Navíc její oblast je stejná jako na základně obrázku.

Možná i průsečík z nějakého úhlu k ose. Potom v průřezu získává ovál nebo jeho část.

Příklady úkolů

Úkol číslo 1. Je uveden přímý válec, jehož základna je 12,56 cm ² . Je třeba vypočítat celkovou plochu válce, pokud je výška 3 cm.

Rozhodnutí. Je nutné použít vzorec pro celou oblast kruhového válce. Ale chybí údaje, a sice poloměr základny. Ale oblast kruhu je známa. Z toho je snadné vypočítat poloměr.

Je rovno druhé odmocnině kvocientu, který se získá dělením plochy základny pi. Po rozdělení 12,56 na 3,14 vyjde 4. Odmocnina kořene 4 je 2. Proto bude mít poloměr přesně tuto hodnotu.

Nyní můžete vypočítat plochu bočního povrchu. Chcete-li to provést, násobte pi podle poloměru, výšky a 2. Práce bude vypadat takto: 3.14 * 3 * 2 * 2. Výsledkem je: 37.68 cm ² .

Chcete-li počítat celkovou plochu, musíte přidat dvě základny (12,56 cm ² ) a boční plochu (37,68 cm ² ). Výsledkem je počet 50,24 cm ² .

Odpověď: S _pohlaví = 50,24 cm ² .

Úkol č. 2. Válec s poloměrem 5 cm je potlačen rovinou rovnoběžnou s osou. Vzdálenost od úseku k ose je 3 cm. Výška válce je 4 cm.

Rozhodnutí. Tvar průřezu je obdélníkový. Jedna strana se shoduje s výškou válce a druhá se rovná akordu. Je-li známa první hodnota, musí být nalezena druhá hodnota.

Chcete-li to provést, proveďte další konstrukci. Na základně tvoříme dva segmenty. Oba začnou uprostřed kruhu. První se bude končit ve středu akordy a bude se rovnat známé vzdálenosti k ose. Druhý je na konci akordy.

Získejte pravý trojúhelník. Je známa hypotenze a jedna z nohou. Hypotenuse se shoduje s poloměrem. Druhá noha je polovina akordy. Neznámé noze, vynásobené 2, dávají požadovanou délku akordy. Vypočítáme jeho hodnotu.

Abyste našli neznámou nohu, musíte napočítat hypotenzu a známou nohu, odečíst druhou od první a oddělit odmocninu. Čtverce jsou 25 a 9. Jejich rozdíl je 16. Po extrakci druhá odmocnina 4. Toto je požadovaná noha.

Chord bude rovnat 4 * 2 = 8 (cm). Nyní můžete vypočítat plochu průřezu: 8 * 4 = 32 (cm ² ).

Odpověď: S _Sich je 32 cm ² .

Úkol číslo 3. Je třeba vypočítat axiální část válce. Je známo, že v ní je zapsána kostka s okrajem 10 cm.

Rozhodnutí. Axiální část válce se shoduje s obdélníkem, který prochází čtyřmi vrcholy krychle a obsahuje úhlopříčky jeho základů. Strana krychle je generátorem válce a diagonál základny se shoduje s průměrem. Produkt těchto dvou veličin udává, že oblast je rozpoznána v problému.

Chcete-li najít průměr, musíte použít vědomí, že na základně krychle je čtverec a jeho úhlopříčka tvoří rovnostranný pravý trojúhelník. Jeho hypotenze je požadovaný diagonální tvar.

Pro jeho výpočet potřebujete vzorec Pythagorovy věty. Je nutné rozdělit stranu krychle, vynásobit ji 2 a extrahovat druhou odmocninu. Deset do druhého stupně je sto. Vynásobeno 2 - 200. Druhá odmocnina 200 je 10√2.

Sekce je opět obdélník s stranami 10 a 10√2. Její plochu lze snadno počítat vynásobením těchto hodnot.

Odpověď zní. S sech = 100/2 cm ² .