Exponentiace: Základní matematika v programování

Často se setkáváme s tím, že potřebujeme zvýšit číslo do jaké míry. Můžete použít obvyklou kalkulačku. Ale to není zajímavé a velmi často neodpovídá podmínkám úkolu.

Pojem matematika

Mělo by začít s vysvětlením matematického významu exponentiace. Například musíme zvýšit nějaký počet x na výkon y. V matematice by tato položka vypadala takto: x ^y = x ^ y. To znamená, že číslo x musí být vynásobeno samotným y časem. Pamatujte, že bez ohledu na to, jakou hodnotu stavíte na nulový stupeň, získáte jeden, a když stavíte na první sílu, získáme původní číslo. Při konstrukci záporného stupně pouze výsledek otočíme.

Exponentiace v pascalu

S matematikou je vše jasné. Ale jak můžeme udělat takový program, který vytvoří exponenciaci? Je to jednoduché. Pokud chceme zvýšit x na hodnotu 5, pak náš kód bude vypadat takto: res: = x * x * x * x * x. Vynásobili jsme počet x pětkrát, protože to bylo pro nás nezbytné, ale co dělat, když nevíme, do jaké míry by mělo být číslo zvýšeno? Dále se podíváme, jak dělat exponentiaci. Pascal nám nedává příliš mnoho příležitostí, ale určitě přijdeme s něčím. Například pomocí standardních funkcí a postupů nebo pomocí různých cyklů.

Squaring číslo

Začněme výstavbou náměstí. Squaring je zvláštní případ exponentiace. Za tímto účelem poskytuje pascal standardní proceduru sqr (x). Zvýší naše číslo x na čtverec, tento záznam se rovná záznamu x * x.

Velmi často to stačí, ale ne vždy program může být omezen pouze na jeden čtverec. Jak vytvořit vyšší stupeň? Přečtěte si o tom a vzdělávejte.

Použití standardních operátorů

V Pascalu existují dvě metody pro zvýšení počtu na výkon: exp (ln (x) * y) a metodu power (x, y). Postup exp () má omezení: x musí být větší než 0, protože není možné extrahovat přirozený logaritmus z nepostavitelného čísla, ale tato funkce je považována za zastaralou a nepohodlnou k použití, proto o ní nebudeme dále mluvit. Funkce power () má dvě hodnoty, první číslo (x) se zvýší na výkon, druhé číslo (y) na výkon, který se má zvednout a vrací x na výkon y. Mělo by být zapamatováno, že čísla x a y jsou skutečné, tj. Skutečné.

Ale existuje jedna nevýhoda, tato funkce není ve všech verzích Pascalu. Každopádně musí být někdy exponentiace prováděna bez použití operátorů. Pokračujte a demontujte následující metodu.

Exponentiace se smyčkou pro

Jak jsme již pochopili, zvýšení čísla na sílu je postupné násobení čísla samo o sobě několikrát. Opakování akce několikrát v programování je mnohem jednodušší než v životě. Použijte smyčku pro:

Rozumíme, co a jak to funguje. Nejprve uvádíme dvě čísla: x a y. Potom jsme jednotku pro výsledek, pro který je - níže. Proveďte cyklus modulu našeho oboru od té doby pokud je stupeň záporný, cyklus nepůjde. V smyčce vynásobíme náš výsledek číslem x samotným. Proč tedy přiřadíme výsledek 1? Za prvé, pokud bychom se vynásobili číslem 0, pak by program vždy dával 0. Za druhé, náš stupeň může být rovný 0, pak by měl program vrátit 1, protože každé číslo v stupni 0 je 1. Poté zkontrolujeme, zda je stupeň negativní nebo pozitivní: pokud je negativní, rozdělíme jednotku o náš výsledek. Provedení tohoto úkolu se smyčkou se provádí v podstatě stejným způsobem.

Použití cyklu while v exponentiaci

Použití cyklu while je správnější než pro, ale předchozí verze je srozumitelnější. Sotva se lze omezit pouze na jednu smyčku, abychom pochopili, že by bylo lepší podívat se na několik příkladů a úkol je nastaven jinak, pro někoho s jedním cyklem, pro někoho jiného, ​​proto budeme analyzovat jinou metodu exponentiace.

Všechno je téměř stejné jako předtím. Zadejte dvě čísla x a y. Hodnotu jednotky přiřadíme k našemu výsledku, aby se zvýšil na nulový stupeň. Potom vytvoříme počítadlo i a přidělíme hodnotě modulu našeho stupně. Cyklus pokračuje, dokud je počitadlo nula, pokud je stupeň od nuly od začátku, cyklus nebude proveden, výsledek zůstane jeden, jak má být, protože libovolné číslo v nulovém stupni je jedno. V samotném cyklu stále považujeme výsledek, vynásobíme-li výsledek, který již získal náš počet x, nezapomeňte odečíst jeden z našeho počitadla, jinak nikdy nedosáhneme nuly. Takže, stejně jako výše, konverze, pokud je stupeň negativní. Není nic komplikovaného, ​​jak se ukázalo. Nikdo však nepochyboval.

No, skončili jsme s obyčejnými čísly, ale nejsou jen taková čísla.

Koncept komplexních čísel

Od samého začátku školního vzdělávání se nám vysvětlují pouze obyčejná čísla, ale existují i ​​další, komplexních čísel. Jsou poměrně obtížně si to představit, zejména vzhledem k tomu, že s nimi téměř nevíme. V matematické notaci mají formu z = x + yi, kde x a y jsou nějaká čísla a i je mentální jednotka. Hned jste si mysleli: toto je běžné číslo, stačí provést operaci přidávání. Ale ne, ne tak jednoduché. Není to součet, je to číslo. Jinými slovy, pokud se pokusíte reprezentovat vše z hlediska geometrie, pak můžete nahradit znaménko přidání středníkem a získáte souřadnice bodu x a y. A pokud budeme stavět nulový vektor k tomuto bodu, pak můžeme vizuálně vidět všechno. Zdá se, že text se stal příliš, uvidíme trochu:

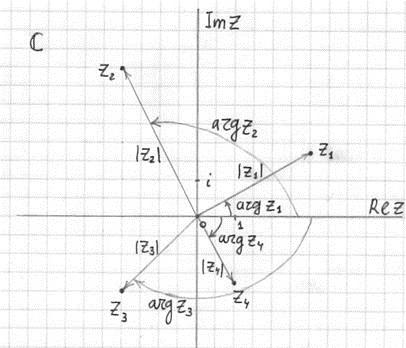
Chceme-li ukázat, že naše letadlo je složité, stačí ho označit smělým písmenem C, jako je tohle. Pak vidíme spoustu bodů, podíváme se na ně a snažíme se pochopit, která z nich je zaznamenána. Vezměte bod z _1, dolů projekci na ose ReZ a dostanete 3, pak na osu lmZ a dostanete 1,75, v důsledku čeho máme číslo z ₁ = 3 + 1,75i. Zdá se, že všechno je jasné, ještě jednou znovu konsolidovat. Bod z ₂ , na vodorovné ose - dvě, ve vertikální - čtyři, v důsledku toho máme: z ₂ = 2 + 4i. Všechno je velmi jasné a jednoduché.

S komplexními čísly jsou možná všechny stejné operace jako u běžných. Přidání, odčítání, násobení, dělení. Ale v tomto článku se zaměříme na konstrukci komplexního čísla na výkon.

Zvyšuje sílu složitého čísla

Co dělat, když potřebujete vytvořit složité číslo? Nestákejte se! Všechno je přesně stejné jako u běžných čísel, ale trochu komplikovanější. Začněme náměstí. Vzhledem k počtu z = 2 + 5i. My čtverci dostaneme z ² = (2 + 5i) ² = (2 + 5i) (2 + 5i) - a to je obvyklé dvoučlenné, můžete se jednoduše množit, dávat podobné pojmy a vše. Je to velmi jednoduché, ale co dělat, když potřebujete stavět do vyššího stupně? Za prvé, naše číslo by mělo být prezentováno v trigonometrické podobě, například:

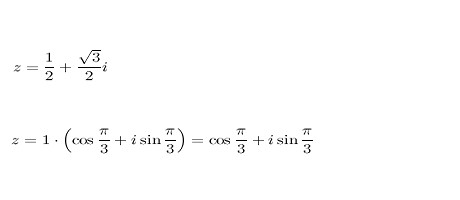
Poté je nutné použít vzorec pro konstrukci komplexních čísel v trigonometrické podobě: z ⁿ = | z | ⁿ * (cos (nx) + i * sin (nx)). Je možné poznamenat, že při konstrukci složitých čísel, a to dokonce i do značné míry, se nemění hodně, takže se nebojte, je to obtížné, ale s praxí vše přijde.

Takže nyní víte, jak zvýšit čísla na sílu v matematice, v programovacím jazyce Pascal, jste se také dozvěděli, jaké složité čísla jsou a jak je postavit na sílu. Všechno se ukázalo jako mnohem jednodušší, než jste si mysleli. Není to tak? Zůstane jen vyzkoušet všechno na vlastní zkušenosti a vše padne na místo. Každá úloha související s exponentiací je nyní pro vás velmi snadná.