Genetické algoritmy: podstata, popis, příklady, aplikace
Myšlenka genetických algoritmů (GA) se objevila již dávno (1950-1975), ale stala se skutečným předmětem studia pouze v posledních desetiletích. D. Holland byl považován za průkopníka v této oblasti, který si vypůjčil hodně genetiky a přizpůsobil ji počítačům. GA jsou široce používány v systémech umělé inteligence, neuronových sítích a optimalizačních problémech.
Evoluční vyhledávání
Modely genetických algoritmů byly vytvořeny na základě evoluce metody volně žijících živočichů a náhodného hledání. Současně je náhodné hledání implementací nejjednodušší evoluční funkce - náhodných mutací a následného výběru.
Z matematického hlediska evoluční hledání znamená nic víc než přeměnu existující konečné sady řešení na novou. Funkcí odpovědnou za tento proces je genetické vyhledávání. Hlavní rozdíl tohoto algoritmu od náhodného hledání je aktivní využití informací shromážděných během iterací (opakování).
Proč potřebujeme genetické algoritmy
GA má tyto cíle:
- vysvětlit adaptační mechanismy jak v přírodním prostředí, tak v intelektuálně-výzkumném (umělém) systému;
- modelování evolučních funkcí a jejich aplikace pro efektivní hledání řešení nejrůznějších problémů, zejména optimalizačních.
V současné době může být podstata genetických algoritmů a jejich modifikovaných verzí nazývána hledáním účinných řešení s ohledem na kvalitu výsledku. Jinými slovy, nalezení nejlepší rovnováhy mezi výkonem a přesností. K tomu dochází díky známému paradigmu "přežití nejschopnějšího jedince" v nejistých a nejasných podmínkách.
Vlastnosti GA
Uvádíme hlavní rozdíly GA od většiny jiných metod nalezení optimálního řešení.
- práce s parametry úkolu, kódované určitým způsobem, a ne přímo s nimi;
- hledání řešení se nevyskytuje stanovením počáteční aproximace, nýbrž v množině možných řešení;
- s využitím pouze objektivní funkce, aniž by se uchýlil k jeho derivacím a úpravám;
- aplikace pravděpodobnostního přístupu k analýze namísto striktně deterministického.
Kritéria výkonnosti
Genetické algoritmy provádějí výpočty na základě dvou podmínek:
- Proveďte zadaný počet iterací.
- Kvalita nalezeného řešení splňuje požadavky.
Pokud je splněna jedna z těchto podmínek, genetický algoritmus přestane provádět další iterace. Navíc použití GA v různých oblastech prostoru řešení jim umožňuje najít mnohem lepší nová řešení, která mají vhodnější hodnoty cílové funkce.
Základní terminologie
Vzhledem k tomu, že GA je založena na genetice, většina terminologie odpovídá. Každý genetický algoritmus funguje na základě počátečních informací. Soubor počátečních hodnot je populace t t = {n 1 , n 2 , ..., n n }, kde n i = {r 1 , ..., r v }. Budeme podrobněji zkoumat:
- t je číslo iterace. t 1 , ..., t k - znamená iteraci algoritmu od čísla 1 do k, a při každé iteraci je vytvořena nová populace řešení.
- n je velikost populace Pt .
- 1 , ..., п i - хромосома, особь, или организм. n 1 , ..., n i - chromozom, jednotlivec nebo organismus. Chromosom nebo řetězec je kódovaná sekvence genů, z nichž každá má sekvenční číslo. Je třeba mít na paměti, že chromozom může být zvláštní případ jednotlivce (organismu).
- r v jsou geny, které jsou součástí kódovaného řešení.
- Lokus je sekvenční číslo genu v chromozomu. Allele je hodnota genu, která může být číselná i funkční.
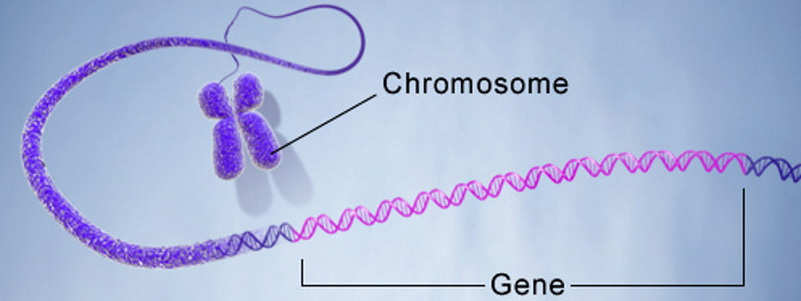
Co znamená "kódované" v kontextu GA? Obvykle je každá hodnota zakódována na základě abecedy. Nejjednodušším příkladem je konverze čísel z desetičlenného číselného systému na binární reprezentaci. Tedy abeceda je reprezentována jako množina {0, 1} a číslo 157 10 bude kódováno chromozomem 10011101 2 , sestávajícím z osmi genů.
Rodiče a potomci
Rodiče jsou prvky vybrané v souladu s danou podmínkou. Například často je tento stav nehodou. Vybrané prvky způsobené operacemi křížení a mutace dávají vzniknout novým, nazývaným potomci. Proto rodiče při realizaci jedné iterace genetického algoritmu vytvářejí novou generaci.
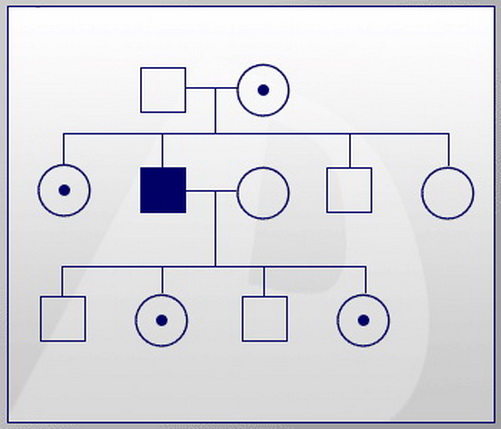
Konečně, vývoj v tomto kontextu bude střídání generací, z nichž každá nová se odlišuje sadou chromozomů, a to kvůli lepší kondici, tj. Vhodnějšímu dodržování stanovených podmínek. Obecné genetické pozadí v procesu evoluce se nazývá genotyp a tvorba spojení organismu s vnějším prostředím se nazývá fenotyp.
Fitness funkce
Kouzlo genetického algoritmu ve funkci fitness. Každý jedinec má svou vlastní hodnotu, kterou lze naučit pomocí funkce adaptace. Jeho hlavním úkolem je vyhodnotit tyto hodnoty pro různé alternativní řešení a zvolit to nejlepší. Jinými slovy, nejschopnější.
V optimalizačních problémech se funkce fitness nazývá cíl, v teorii řízení se nazývá chyba, v teorii her je funkcí hodnoty a tak dále. Co přesně bude reprezentováno jako funkce adaptace závisí na problému, který má být vyřešen.
Nakonec lze konstatovat, že genetické algoritmy analyzují populaci jedinců, organismů nebo chromozomů, z nichž každá je reprezentována kombinací genů (soubor některých hodnot) a hledá optimální řešení, které mezi sebou přeměňují jedince obyvatelstva.
Odchylky v jednom směru jednotlivých prvků v obecném případě jsou v souladu s běžným zákonem o distribuci veličin. Současně GA poskytuje dědičnost vlastností, z nichž nejvhodnější jsou fixní, čímž poskytuje nejlepší populaci.
Základní genetický algoritmus
Postupně rozkládáme nejjednodušší (klasické) GA.
- Inicializace počátečních hodnot, tj. Definice primární populace, soubor jedinců, se kterými se evoluce projeví.
- Stanovení primární způsobilosti každého jednotlivce v populaci.
- Zkontrolujte podmínky ukončení iterací algoritmu.
- Použití funkce výběru.
- Použití genetických operátorů.
- Vytvoření nové populace.
- Kroky 2-6 se opakují v cyklu, dokud není splněna nezbytná podmínka, po které se objeví výběr nejvhodnějších osob.
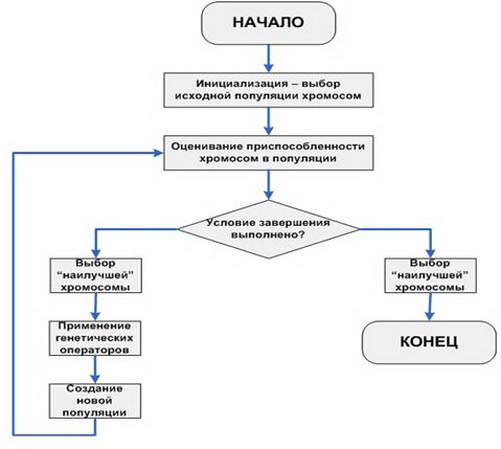
Pojďme si krátce projít trochu zřejmými částmi algoritmu. Existují dvě podmínky pro ukončení:
- Počet iterací.
- Kvalita řešení.
Genetickými operátory jsou operátory mutace a operátor přechodu. Mutace změní náhodné geny s jistou pravděpodobností. Pravděpodobnost mutace má zpravidla nízkou číselnou hodnotu. Promluvme si o postupu genetického algoritmu "crossing". Vyskytuje se podle následující zásady:
- Pro každý pár rodičů obsahujících L geny je náhodně vybrán přechodový bod Tsk i .
- První potomka je složena spojením [1; Tsk i ] genů prvního rodiče [Tsk i + 1 ; L] genů druhého rodiče.
- Druhý potomk je složen v opačném směru. Nyní k genům druhého rodiče [1; Tsk i ] přidává geny prvního rodiče do pozic [Tsk i + 1 ; L].
Triviální příklad
Problém řešíme pomocí genetického algoritmu, který používá příklad hledání jedince s maximálním počtem jednotek. Nechte jednotlivce sestávat z 10 genů. Primární populaci přidělujeme ve výši osmi osob. Je zřejmé, že nejlepší osobou by měla být 1111111111. Vyrovnejme rozhodnutí GA.
- Inicializace. Vyberte 8 náhodných jednotlivců:
| n 1 | 1110010101 | n 5 | 0101000110 |
| n 2 | 1100111010 | n 6 | 0100110101 |
| n 3 | 1110011110 | n 7 | 0110111011 |
| n 4 | 1011000000 | n 8 | 0100001001 |
- Posouzení způsobilosti. Je zřejmé, že v našem genetickém algoritmu bude fitness funkce F počítat počet jednotek v každém jednotlivci. Proto máme:
| n i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F (n i ) | 6 | 7 | 8 | 3 | 4 | 5 | 7 | 3 |
Tabulka ukazuje, že jednotlivci 3 a 7 mají největší počet jednotek, a proto jsou nejvhodnějšími členy populace k vyřešení problému. Vzhledem k tomu, že v současné době neexistuje řešení požadované kvality, algoritmus nadále funguje. Je nutné provést výběr jednotlivců. Pro snadné vysvětlení nechte výběr být náhodný a získáme vzorek jedinců {n 7 , n 3 , n 1 , n 7 , n 3 , n 7 , n 4 , n 2 } - to jsou rodiče pro novou populaci.
- Použití genetických operátorů. Zjednodušeně předpokládáme, že pravděpodobnost mutací je 0. Jinými slovy, všech 8 jedinců předává své geny tak, jak jsou. Pro křížení vytvoříme dvojice jednotlivců náhodně: (n 2 , n 7 ), (n 1 , n 7 ), (n 3 , n 4 ) a (n 3 , n 7 ). Stejným náhodným způsobem jsou vybrány body přechodu pro každý pár:
| Pár | (p 2 , p 7 ) | (n1, n7) | (p 3 , p 4 ) | (p 3 , p 7 ) |
| Rodiče | [1100111010] [0110111011] | [1110010101] [0110111011] | [1110011110] [1011000000] | [1110011110] [0110111011] |
| Tsk i | 3 | 5 | 2 | 8 |
| Potomci | [1100111011] [0110111010] | [1110011011] [0110110101] | [1111000000] [1010011110] | [1110011111] [0110111010] |
- Kompilace nové populace sestávající z potomků:
| n 1 | 1100111011 | n 5 | 1111000000 |
| n 2 | 0110111010 | n 6 | 1010011110 |
| n 3 | 1110011011 | n 7 | 1110011111 |
| n 4 | 0110110101 | n 8 | 0110111010 |
- Odhadujeme vhodnost každého jednotlivého nového obyvatelstva:
| n i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F (n i ) | 7 | 6 | 7 | 6 | 4 | 6 | 8 | 6 |
Další akce jsou zřejmé. Nejzajímavější v GA je, když odhadujeme průměrný počet jednotek v každé populaci. V první populaci bylo v průměru 5 375 jednotek u každého jednotlivce, v populaci potomků - 6,25 jednotek na osobu. A takový rys bude pozorován, i když během mutací a překročení je ztracena osoba s největším počtem jednotek v první populaci.
Implementační plán
Vytvoření genetického algoritmu je poměrně komplikovaným úkolem. Zaprvé uvedeme plán v podobě kroků, po kterém podrobněji prozkoumáme každý z nich.
- Definice reprezentace (abeceda).
- Definice operátorů náhodných změn.
- Definice přežití jednotlivců.
- Generace primární populace.
První fáze říká, že abeceda, ve které budou zakódovány všechny prvky množiny řešení nebo populace, musí být dostatečně flexibilní, aby bylo možné současně provést nezbytná náhodná permutace a vyhodnotit vhodnost elementů, primárních i těch, které prošly změnami. Je matematicky stanoveno, že pro tyto účely nelze vytvořit ideální abecedu, a proto je její kompilace jedním z nejtěžších a nejdůležitějších kroků k zajištění stabilního fungování GA.

Rovněž je obtížné definovat výkazy změn a vytvářet potomky. Existuje mnoho operátorů, kteří jsou schopni provést požadované akce. Například je z biologie známo, že každý druh se může rozmnožovat dvěma způsoby: sexuálně (křížením) a asexuální (mutací). V prvním případě si rodiče vyměňují genetický materiál, ve druhém dochází k mutacím, určeným vnitřními mechanismy těla a vnějším vlivem. Kromě toho mohou být použity reprodukční modely, které neexistují ve volné přírodě. Používejte například geny tří nebo více rodičů. Podobně překročení mutace v genetickém algoritmu může zahrnovat různorodý mechanismus.
Volba metody přežití může být extrémně zavádějící. V genetickém algoritmu pro chov je mnoho způsobů. A jak ukazuje praxe, pravidlo "přežití nejschopnějších" není vždy nejlepší. Při řešení složitých technických problémů se často ukazuje, že nejlepší řešení pochází z množství středních nebo dokonce horších. Proto je často akceptováno používání pravděpodobnostního přístupu, který uvádí, že nejlepší řešení má větší šanci na přežití.

Poslední etapa poskytuje flexibilitu algoritmu, který nikdo jiný nemá. Počáteční populace řešení může být definována buď na základě jakýchkoli známých údajů nebo zcela náhodným způsobem jednoduše přeskupením genů uvnitř jedinců a vytvořením náhodných jedinců. Je však vždy zapotřebí pamatovat na to, že účinnost algoritmu závisí na počáteční populaci.
Účinnost
Účinnost genetického algoritmu zcela závisí na správnosti kroků popsaných v plánu. Zvláště důležitým faktorem je vytvoření primární populace. Existuje mnoho přístupů k tomuto. Popisujeme několik:
- Vytvoření úplné populace, která bude zahrnovat nejrůznější možnosti pro jednotlivce v dané oblasti.
- Náhodná tvorba jednotlivců založená na všech platných hodnotách.
- Dot náhodné vytvoření jednotlivců, když mezi přijatelnými hodnotami je vybrán rozsah pro generaci.
- Kombinace prvních tří způsobů vytvoření populace.

Můžeme tedy konstatovat, že účinnost genetických algoritmů závisí do značné míry na zkušenostech programátora v této věci. To je jak nevýhoda genetických algoritmů, tak jejich výhoda.