Jak je formulovaná a prokázána kosinová věta?
Ne všichni školáci, a ještě víc dospělí, vědí, že cosinální teorém je přímo spojen s Pythagorovou větu. Přesněji řečeno jde o zvláštní případ prvního. Tento okamžik, stejně jako dva způsoby, jak prokázat větu kosinusu, vám pomohou stát se znalější osobou. Kromě toho praxe vyjadřování hodnot z původních výrazů je dobře vyvinuté logické myšlení. Dlouhý vzorec studované věty jistě nutí člověka, aby pracoval a zlepšoval.
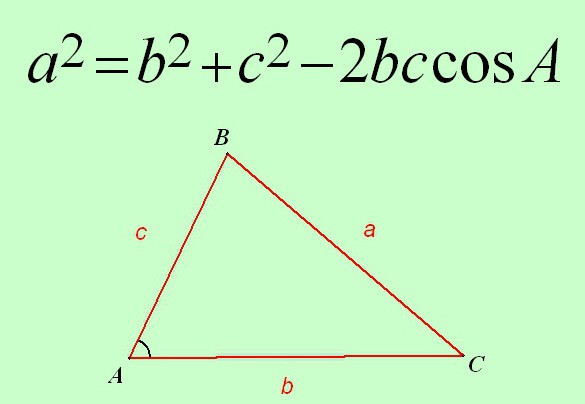
Začátek rozhovoru: zavedení symbolů
Tato věta je formulována a prokázána pro libovolný trojúhelník. Proto může být vždy použita v každé situaci, pokud jsou dány dvě strany a v některých případech tři a úhel, a ne nutně mezi nimi. Cokoliv druh trojúhelníku věta vždy funguje.
A nyní o určení množství ve všech výrazech. Je lepší souhlasit najednou, aby to nebylo několikrát vysvětleno. K tomu je sestavena následující tabulka.
| Prvek trojúhelníku | Jeho označení |
| Neznámá strana | a |
| Dvě další strany | in, s |
| Úhel proti nepoznané straně | A |
| Úhly, které leží na jiných stranách | B, C |
| Výška vrcholu trojúhelníku | n |
Formulace a matematické psaní
Takže věta kosinus je formulována takto:
Čtverec strany libovolného trojúhelníku se rovná součtu čtverců na ostatních dvou stranách, minus dvojnásobek produktu na stejných stranách kosinus úhlu ležícího mezi nimi.
Samozřejmě, je to dlouhé, ale pokud pochopíte jeho podstatu, pak bude snadno zapamatovatelné. Můžete si dokonce představit výkres trojúhelníku. Vizuálně vždy snazší zapamatovat si.
Vzorec této věty bude vypadat takto:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Trochu dlouho, ale všechno je logické. Pokud se podíváte trochu blíž, můžete vidět, že se písmena opakují, takže je snadné si je pamatovat.
Společný důkaz věty
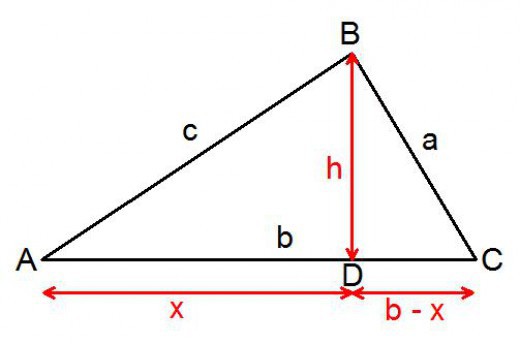
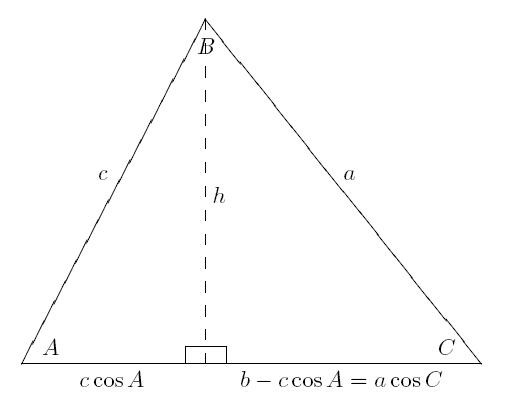
Vzhledem k tomu, že je platné pro všechny trojúhelníky, je možné zvolit odůvodnění jakéhokoli typu. Nechte to být postava se všemi ostrými rohy. Zvažte libovolný akustický trojúhelník, jehož úhel C je větší než úhel B. Z vrcholu s tímto velkým úhlem musíte snížit kolmo na protilehlou stranu. Výška držená dělí trojúhelník na dva obdélníkové. To je nutné pro důkaz.
Strana bude rozdělena na dva segmenty: x, y. Musí být vyjádřeny známými termíny. Část, která se ukáže být v trojúhelníku s hypotenzí rovnou, bude vyjádřena psaním:
x = in * cos A.
Druhý se bude rovnat tomuto rozdílu:
y = s - in * cos A.
Teď potřebujeme zapsat Pythagorovu větu pro výsledné dvě pravé trojúhelníky s neznámou výškou. Tyto vzorce budou vypadat takto:
n 2 = v 2 - (v * cos A) 2 ,
n 2 = a 2 - (c - c * cos A) 2 .
V těchto rovnicích jsou shodné výrazy vlevo. Proto budou jejich pravé strany rovny. Je snadné psát. Nyní musíte otevřít závorky:
ve 2 - v 2 * (cos A) 2 = a 2 - c 2 + 2 c * v * cos A - v 2 * (cos A) 2 .
Pokud provedeme převod a redukci takových termínů, získáme počáteční vzorec, který je napsán po znění, tj. Kosinové věty. Doklad je úplný.
Důkaz věty prostřednictvím vektorů
Je mnohem kratší než předchozí. A pokud znáte vlastnosti vektorů, pak se kosinová věta pro trojúhelník jednoduše osvědčí.
Pokud jsou strany a, b, c označené vektory BC, AC a AB, potom platí rovnost:
SU = AC - AB.
Nyní musíte provést některé akce. První z nich je na obou stranách rovnosti:
BC 2 = AC 2 + AB 2 - 2 AC * AB.
Pak musí být rovnost přepsána ve skalární podobě, jelikož produkt vektorů se rovná kosinusu úhlu mezi nimi a jejich skalárními hodnotami:
BC 2 = AC 2 + AB 2 - 2 AC * AB * cos A.
Zbývá jen vrátit se k starému zápisu a znovu se objeví cosinální věta:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Vzorce pro jiné strany a všechny úhly
Chcete-li najít stranu, z kosinové věty je třeba extrahovat druhá odmocnina. Vzorec pro čtverce jedné z ostatních stran bude vypadat takto:
s 2 = a 2 + až 2 - 2 * a * to * cos.
Chcete-li napsat výraz pro čtverec strany, je nutné předešlou rovnost nahradit z az a naopak a uvést úhel B pod kosinus
Ze základního vzorce věty můžeme vyjádřit hodnotu kosinusu úhlu A:
cos A = (v 2 + c 2 - a 2 ) / (2 v * s).
Vzorce pro jiné úhly jsou odvozeny stejným způsobem. To je dobrá praxe, takže se můžete pokusit sami napsat.
Samozřejmě není nutné tyto vzorce zapamatovat. Stačí pochopit větu a schopnost odvodit tyto výrazy z jejího hlavního záznamu.
Původní vzorec věty umožňuje najít stranu, pokud úhel není mezi dvěma známými. Například, musíte najít v , když daný hodnoty: a, c, a . Nebo je to neznámý, ale existují hodnoty a, b, a .
V této situaci je nutné přesunout všechny přídatné vzorce doleva. Tato rovnost je dosažena:
c 2 - 2 * c * c * cos A + v 2 - a 2 = 0.
Přepište jej trochu jinou formou:
s 2 - (2 * v * cos A) * s + (v 2 - a 2 ) = 0.
Můžete snadno vidět kvadratickou rovnici. V něm je neznámé množství c , a všechny ostatní jsou dány. Proto je postačující vyřešit to s pomocí diskriminace. Takže neznámá strana bude nalezena.
Podobně vzorec pro druhou stranu je získán:
2 - (2 * s * cos A) * c + (c 2 - a 2 ) = 0.
Z jiných výrazů se tyto vzorce také snadno dostanou.
Jak vypočítat úhel bez výpočtu kosinusu?
Pokud se podíváte blíže na vzorec úhlu kosinusu, který byl odvozen dříve, zjistíte následující:
- jmenovatel zlomku je vždy kladným číslem, protože obsahuje produkt stran, který nemůže být negativní;
- úhel bude záviset na znaménku čitatele.
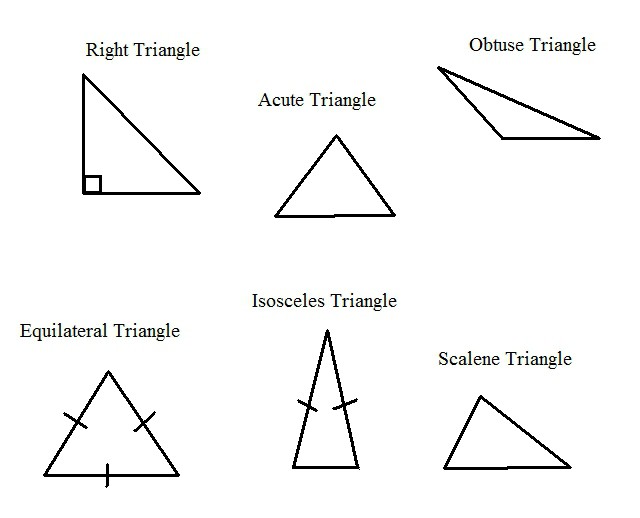
Úhel A bude:
- akutní v situaci, kdy čitatel je větší než nula;
- pokud je tento výraz záporný;
- přímý, když je nulový.
Mimochodem, poslední situace změní kosinkovou větu na Pythagorovu větu. Protože u úhlu 90 ° je jeho kosinus nula a poslední termín zmizí.
První úkol
Stav
Tupý úhel libovolného trojúhelníku je 120 °. O stranách, na které je omezeno, je známo, že jeden z nich je o 8 cm delší než druhý, délka třetí strany je známá, je 28 cm, je nutné najít obvod trojúhelníku.
Řešení
Nejprve musíte označit jednu ze stran písmenem "x". V tomto případě se druhá rovná (x + 8). Vzhledem k tomu, že existují výrazy pro všechny tři strany, můžete použít vzorec, který kosínová věta dává:
28 2 = (x + 8) 2 + x 2 - 2 * (x + 8) * x * cos 120 °.
V tabulkách pro cosinus musíte najít hodnotu odpovídající 120 stupňům. To bude číslo 0,5 s znaménkem mínus. Nyní je nutné otevřít závorky, dodržovat všechna pravidla a poskytnout podobné pojmy:
784 = x 2 + 16 x + 64 + x 2 - 2x * (-0,5) * (x + 8);
784 = 2x 2 + 16x + 64 + x 2 + 8x;
3x 2 + 24x - 720 = 0.
Tato kvadratická rovnice je řešena nalezením diskriminačního, který se bude rovnat:
D = 24 2 - 4 * 3 * (- 720) = 9216.
Vzhledem k tomu, že její hodnota je větší než nula, rovnice má dvě kořenové odpovědi.
x 1 = ((-24) + √ (9216)) / (2 * 3) = 12;
x 2 = ((-24) - √ (9216)) / (2 * 3) = -20.
Poslední kořen nemůže být odpovědí na problém, protože strana musí být nutně pozitivní.
Takže jsou známé dvě strany. Snadné najít třetí: 12 + 8 = 20 (cm). Nyní můžete odpovědět na otázku problému. Obvod trojúhelníku je definován jako součet všech stran:
24 + 12 + 20 = 60 (cm).
Odpověď : obvod je 60 centimetrů.

Číslo problému 2
Stav
V trojúhelníku jsou známy: c , rovný 2 cm; a , což je 10 cm; úhel C hodnota 120 °. Požadováno, aby se našla strana.
Řešení
Nejprve musíte použít větu cosine a odvodit vzorec kvadratická rovnice v níž bude hodnota neznámá:
s 2 = a 2 + ve 2 - 2 * a * v * cos C
a
ve 2 - (2 * a * cos C) * v + (a 2 - c 2 ) = 0.
Ve stavu je nutné nahradit všechny známé hodnoty:
ve 2 - (2 * 10 * cos 120 °) * v + (10 2 - 2 2 ) = 0.
Nyní musíme počítat, co je možné zjednodušit výraz:
v 2 - (20 * (-1/2)) * v + (100 - 4) = 0
nebo
v 2 + 10 * in - 96 = 0.
Jedná se o standardní kvadratickou rovnici, kterou je třeba vyřešit nalezením diskriminačního:
D = (10) 2 - 4 * 1 * (-96) = 484.
Podle vzorců je třeba provést výpočty pro neznámou stranu:
v 1 = (- 10 + 22) / 2 = 6 (cm);
v 2 = (- 10 - 22) / 2 = - 16 - tento kořen nevyhovuje řešení problému, protože strana nemůže být negativní.
Odpověď: neznámá strana je 6 cm.
Třetí úkol
Stav
V trojúhelníku jsou boky: a, b, c , které jsou 6 cm, 10 cm a 8 cm. Je třeba vypočítat úhel A.
Řešení
Opět musíte použít cosinální větu. Použije se jeho záznam, ve kterém je kosinus úhlu A, protože právě to musí být vypočítáno. Zde je vzorec pro kosinus neznámého úhlu:
cos A = (v 2 + c 2 - a 2 ) / (2 v * s).
Zbývá nahradit hodnoty stran a provádět všechny výpočty:
cos A = (10 2 + 8 2 - 6 2 ) / (2 x 8 x 10).
Po ukončení všech termínů a vynásobení čísel z jmenovatele:
cos A = (100 + 64 - 36) / (160).
Po přidání a rozdělení se ukáže:
cos A = 128/160 = 0,8.
Nyní musíte použít tabulku Bradis, abyste zjistili, jaký je úhel A. Nejbližší hodnota úhlu pro tento kosinus je 36 ° 54 '.
Odpověď: hodnota úhlu A je 36 ° 54 '.