Jak vypočítat plochu trojúhelníku
Trojúhelník je dobře známá postava. A to navzdory bohaté různorodosti jeho forem. Obdélníkový, rovnostranný, akutní, rovnostranný, tupý. Každý z nich je jiný. Ale pro každého, kdo potřebuje poznat oblast trojúhelníku.
Společné pro všechny vzorce trojúhelníků, které používají délku stran nebo výšky
Označení přijatá v nich: strany - a, b, c; výšky na odpovídajících stranách n, n, in , n s .
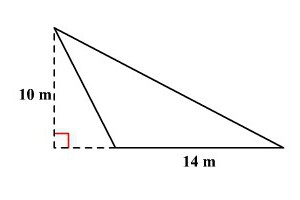
1. Plocha trojúhelníku se vypočítá jako produkt ½, boky a výška spuštěná na něm. S = ½ * a * n a . Podobně byste měli napsat vzorec pro ostatní dvě strany.
2. Heronův vzorec, ve kterém se objevuje poloprůchod (obvykle je označen písmenem p, na rozdíl od plného obvodu). Semi-perimetr musí být počítán následovně: položte všechny strany dohromady a rozdělujte je o 2. Polopříměrový vzorec: p = (a + b + c) / 2. Pak rovnost pro oblast obrázku vypadá takto: S = √ (p * p - c) * (p - c)).
3. Pokud nechcete použít poloprůchod, pak je užitečný vzorec, ve kterém jsou přítomny pouze délky stran: S = ¼ * √ ((a + b + c) * (b + c - a) (a + b - c)). Je poněkud delší než předchozí, ale pomůže, pokud jste zapomněli, jak najít poloprůhled.
Obecné vzorce, ve kterých se objevují úhly trojúhelníku
Označení, která jsou potřebná ke čtení vzorců: α, β, γ - úhly. Leží naproti stranám a, b, c, resp.
1. Podle něj polovina výrobku ze dvou stran a sinus úhlu mezi nimi je rovna ploše trojúhelníku. To znamená: S = ½ a * b * sin γ. Podobně by měly být formulovány další dva případy.
2. Plochu trojúhelníku lze vypočítat jednou stranou a třemi známými úhly. S = (a 2 * sin β * sin γ) / (2 sin α).
3. Existuje také vzorec s jednou známou stranou a dvěma koutky sousedícími s ním. Vypadá to takto: S = c 2 / (2 (ctg α + ctg β)).
Poslední dvě vzorce nejsou nejsnadnější. Zapamatujte si je docela obtížné.
Obecné vzorce pro situaci, kdy jsou známy poloměry zapsaných nebo ohraničených kružnic.
Další označení: r, R - poloměry. První se používá pro poloměr zapsaného kruhu. Druhý je pro popis.
1. První vzorec, podle kterého je vypočtený prostor trojúhelníku, je spojen s poloprůchodem. S = p * r. Jiným způsobem lze psát následovně: S = ½ r * (a + b + c).
2. V druhém případě budete muset vynásobit všechny strany trojúhelníku a rozdělit je čtyřnásobným poloměrem obrysu. Z doslovného hlediska to vypadá takto: S = (a * c * s) / (4R).
3. Třetí situace vám umožňuje dělat bez znalosti stran, ale budou vyžadovány hodnoty všech tří úhlů. S = 2 R2 2 sin sin * sin β * sin γ.
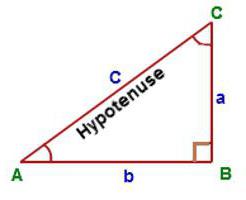
Zvláštní případ: pravý trojúhelník
Jedná se o nejjednodušší situaci, protože vyžaduje znalost pouze délky obou nohou. Označují latinské písmena a a c. Oblast pravého trojúhelníku se rovná polovině plochy dokončeného obdélníku.
Matematicky to vypadá takto: S = ½ a * c. To je nejlépe zapamatováno. Vzhledem k tomu, že vypadá jako vzorec pro oblast obdélníku, objeví se pouze další zlomek, což znamená polovinu.
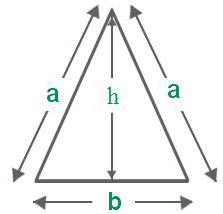
Zvláštní případ: rovnoramenný trojúhelník
Vzhledem k tomu, že má dvě stejné strany, některé vzorce pro svou oblast vypadají poněkud zjednodušené. Například Heronův vzorec, který počítá plochu rovnoramenného trojúhelníku, má následující podobu:
S = ½ v √ (((a + ½ in)) * (a - ½ palce)).
Převedete-li to, bude kratší. V tomto případě je Heronův vzorec pro rovnoramenný trojúhelník napsán jako:
S = v √ (4 * a 2 - b 2 ).
Poněkud jednodušší než u libovolného trojúhelníku, oblastní vzorec vypadá, jako by byly známé strany a úhel mezi nimi. S = ½ a 2 * sin β.
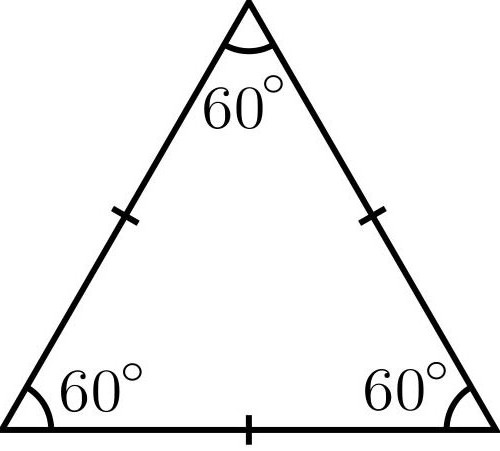
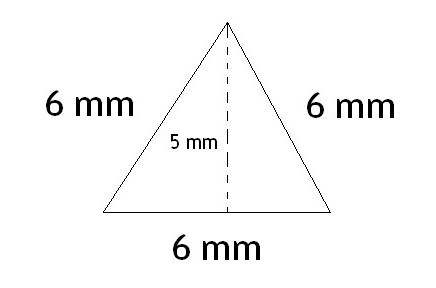
Zvláštní případ: rovnostranný trojúhelník
Obvykle v problémech o něm je známá strana nebo můžete nějak zjistit. Pak vzorec, který je oblastí takového trojúhelníku, vypadá takto:
S = (a 2 √3) / 4.
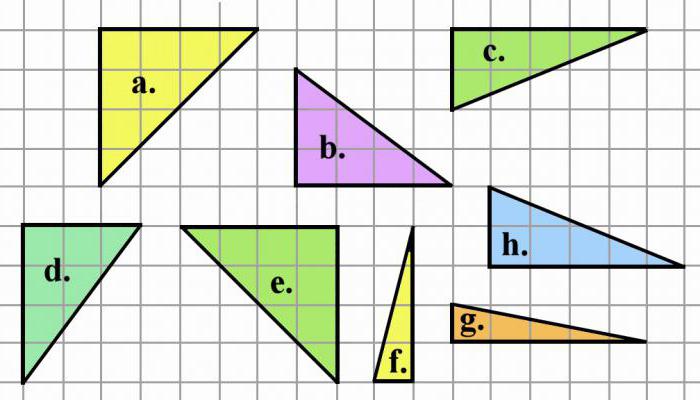
Úkoly při hledání oblasti, je-li trojúhelník zobrazen na kartonovém papíru
Nejjednodušší je situace, kdy je nakreslen pravý trojúhelník, takže jeho nohy se shodují s čarami papíru. Pak stačí započítat počet buněk, které se vejde do nohou. Pak je vynásobte a rozdělte dvěma.
Pokud je trojúhelník akutní nebo tupý, musí být přitahován k obdélníku. Pak ve výsledném tvaru budou 3 trojúhelníky. Jeden je ten, který je uveden v problému. A další dva - pomocné a obdélníkové. Určete oblast posledních dvou potřeb výše uvedené metody. Poté počítáme plochu obdélníku a odečteme od něj ty, které jsou vypočítány pro pomocné zařízení. Oblast trojúhelníku je definována.
Mnohem obtížnější je situace, kdy se ani jedna strana trojúhelníku neshoduje s linií papíru. Poté musí být zapsán do obdélníku, takže vrcholy původní postavy leží na jeho stranách. V tomto případě budou tři pomocné pravé trojúhelníky.
Příklad problému na vzorec Gerona
Stav Některé trojúhelníky mají strany. Jsou to 3, 5 a 6 cm. Musíte vědět jeho oblast.
Rozhodnutí. Především je nutné počítat poloprůchod trojúhelníku. Vypočtěte součet všech tří, dané v problému, čísla a rozdělte jej na dvě. Jednoduché výpočty vedou k číslu 7. To je hodnota poloměru.
Nyní můžete vypočítat plochu trojúhelníku pomocí výše uvedeného vzorce. Pod druhá odmocnina Objeví se produkt čtyř čísel: 7, 4, 2 a 1. To znamená, že oblast je √ (4 * 14) = 2 √ (14).
Pokud není požadována větší přesnost, můžete extrahovat druhou odmocninu 14. Je rovno 3,74. Pak se plocha rovná 7,48.
Odpověď zní. S = 2 √ 14 cm 2 nebo 7,48 cm 2 .
Příklad problému s pravým trojúhelníkem
Stav Jedna noha pravého trojúhelníku je o 31 cm delší než druhá. Musíte znát jejich délky, pokud je oblast trojúhelníku 180 cm2.
Rozhodnutí. Musíme vyřešit systém dvou rovnic. První se týká náměstí. Druhý je s postojem nohou, který je uveden v problému.
180 = ½ a * c;
a = při +31.
Nejprve musí být hodnota "a" nahrazena první rovnicí. Ukazuje se: 180 = ½ (v + 31) * c. Má pouze jedno neznámé množství, takže je snadné jej vyřešit. Po otevření držáků je získána kvadratická rovnice: v 2 + 31 in - 360 = 0. Dává dvě hodnoty pro "in": 9 a - 40. Druhé číslo neodpovídá odpovědi, protože délka strany trojúhelníku nemůže být záporná.
Zbývá vypočítat druhou nohu: přidat k získanému číslu 31. Ukázalo se, že se jedná o množství, o které se v tomto problému pokouší.
Odpověď zní. Nohy trojúhelníku jsou 9 a 40 cm.
Úkolem nalezení strany přes oblast, stranu a úhel trojúhelníku
Stav Plocha trojúhelníku je 60 cm2. Je třeba vypočítat jednu ze stran, pokud je druhá strana 15 cm a úhel mezi nimi je 30 °.
Rozhodnutí. Na základě přijatého zápisu je požadovaná strana "a", známá "in", daný úhel "γ". Pak může být vzorec oblasti přepsán takto:
60 = ½ a * 15 * sin 30 °. Zde je sinus 30 stupňů 0,5.
Po transformaci se "a" rovná 60 / (0,5 x 0,5 x 15). To je 16.
Odpověď zní. Požadovaná strana je 16 cm.
Problém čtverce v pravém trojúhelníku
Stav Horní část čtverce se stranou 24 cm se shoduje s pravým úhlem trojúhelníku. Dva další leží na nohách. Třetí patří k hypotenze. Délka jedné nohy je 42 cm. Jaká je oblast pravoúhlého trojúhelníku?
Rozhodnutí. Zvažte dva pravé trojúhelníky. První je uvedena v úloze. Druhý je založen na známé noze původního trojúhelníku. Jsou podobné, protože mají společný úhel a jsou tvořeny rovnoběžnými čarami.
Potom jsou vztahy jejich nohou stejné. Nohy menšího trojúhelníku jsou 24 cm (strana náměstí) a 18 cm (daná noha 42 cm odečíst na straně čtverce 24 cm). Odpovídající nohy velkého trojúhelníku jsou 42 cm a x cm. Toto je "x", které je potřebné pro výpočet plochy trojúhelníku.
18/42 = 24 / x, tj. X = 24 * 42/18 = 56 (cm).
Pak se plocha rovná produkci 56 a 42, rozdělené na dvě, tj. 1176 cm2.
Odpověď zní. Požadovaná plocha je 1176 cm 2 .