Jak zjistit délku oblouku kruhu

Vzorec pro zjištění délky oblouku kruhu je poměrně jednoduchý a velmi často na důležitých zkouškách, jako je jednotná státní zkouška, existují takové problémy, které nelze vyřešit bez jeho použití. Také je třeba znát pro předání mezinárodních standardizovaných testů, jako je SAT a další.

Jaká je délka oblouku kruhu?

Vzorec je následující:

l = πrα / 180 °

Jaký je každý z prvků vzorce:

• l je délka oblouku kruhu;
• π je číslo pi (konstantní hodnota rovná ≈ 3,14);
• r je poloměr daného kruhu;
• α je hodnota úhlu, na kterém spočívá oblouk (spíše centrální než zapsaná).

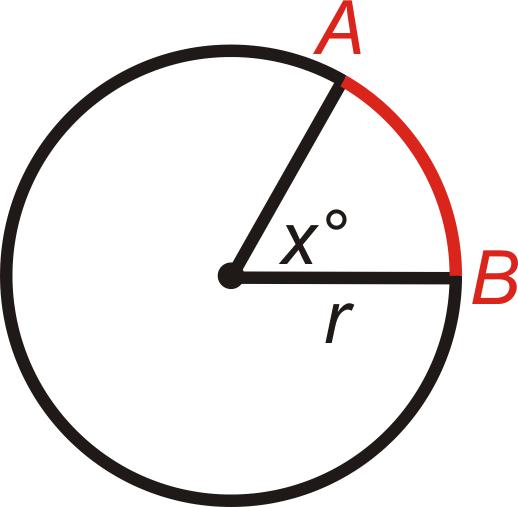
Jak je vidět, k vyřešení problému musí podmínka obsahovat r a α. Bez těchto dvou hodnot nelze najít délku oblouku.

Jak je tento vzorec odvozen a proč to vypadá takto?

Všechno je velmi snadné. Bude to mnohem jasnější, pokud v jmenovateli umístíte 360 ​​° a v čitateli v přední části přidáte číslo. Nemůžete také opustit zlomek, stahovat je a psát násobením. Je docela možné si dovolit, protože tento prvek je v čitateli. Pak bude obecný pohled:

l = (2πr / 360 °) × α

Jen pro pohodlí, snížené o 2 a 360 °. A teď, když se podíváte pozorně, můžete si všimnout velmi známého vzorce pro délku celého kruhu, jmenovitě 2πr. Celý kruh se skládá z 360 °, protože dělíme získanou míru na 360 částí. Pak se množíme číslem α, tedy číslem "kusů koláče", které potřebujeme. Ale každý ví jistě, že číslo (tj. Délka celého kruhu) nemůže být děleno stupněm. Co dělat v tomto případě? Obvykle je zpravidla stupeň snižován se stupněm centrálního úhlu, tedy s α. Koneckonců zůstanou pouze čísla a výsledkem je konečná odpověď.

To může vysvětlit, proč délka oblouku kruhu je tímto způsobem a má tuto formu.

Příklad problému s průměrnou složitostí pomocí tohoto vzorce

Stav: Kruh s poloměrem 10 centimetrů. Stupeň měření středního úhlu je 90 °. Najděte délku oblouku kruhu tvořeného tímto úhlem.

Řešení: l = 10π × 90 ° / 180 ° = 10π × 1/2 = 5π

Odpověď: l = 5π

Je také možné, že namísto míry míry by byla dána míra radiálního úhlu. V žádném případě se nebojte, protože tentokrát je úkol mnohem jednodušší. Chcete-li převést radian na stupeň měření, musíte toto číslo vynásobit o 180 ° / π. Takže nyní můžete nahradit následující kombinaci namísto α : m × 180 ° / π. Kde m je hodnota radiánu. A pak 180 a počet π se sníží a získá se úplně zjednodušený vzorec, který vypadá následovně:

l = mr,

kde:

• l je délka oblouku kruhu;
• m je radian měřítko úhlu;
• r je poloměr daného kruhu.