Jak najít poloměr kruhu. Vložený a ohraničený kruh

Poloměr je segment, který spojuje jakýkoli bod v kruhu s jeho středem. Jedná se o jednu z nejdůležitějších vlastností tohoto čísla, protože na základě toho můžete vypočítat všechny ostatní parametry. Pokud víte, jak najít poloměr kruhu, můžete vypočítat jeho průměr, délku a plochu. V případě, že je toto číslo zapsáno nebo popsáno kolem jiného, ​​lze vyřešit řadu úkolů. Dnes zkoumáme základní vzorce a rysy jejich aplikace.

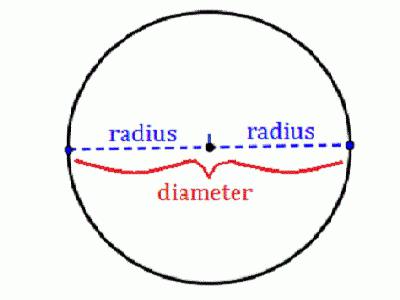
Známé hodnoty

Pokud víte, jak najít poloměr kruhu, který je obvykle označen písmenem R, pak jej lze vypočítat z jedné charakteristiky. Tyto hodnoty zahrnují:

• obvod (C);
• průměr (D) je segment (nebo spíše akord), který prochází středem;
• oblast (S) - prostor, který je omezen na tuto hodnotu.

Podél obvodu

Pokud je hodnota C známá v problému, pak R = C / (2 * P). Tento vzorec je odvozen. Pokud víme, co to je délka obvodu pak to nemusí pamatovat. Předpokládejme, že v problémech C = 20 m. Jak najít poloměr kruhu v tomto případě? Jednoduše nahraďte známou hodnotu ve výše uvedeném vzorci. Všimněte si, že v takových problémech vždy vyplývá znalost čísla P. Pro lepší výpočet hodnotíme hodnotu 3.14. Řešení v tomto případě je následující: zapište, jaké hodnoty jsou uvedeny, odvodte vzorec a proveďte výpočty. V odpovědi píšeme, že poloměr je 20 / (2 * 3,14) = 3,19 m. Je důležité nezapomínat na to, co jsme si mysleli a zmínili se o názvu jednotek měření.

Podle průměru

Okamžitě zdůrazňujeme, že je to nejjednodušší typ problému, který se ptá, jak najít poloměr kruhu. Pokud dostanete takový příklad na kontrolu, pak můžete být klidní. Nepotřebuje ani kalkulačku! Jak již bylo řečeno, průměr je segment nebo, správněji, akord, který prochází středem. Navíc jsou všechny body kruhu stejné. Proto se tento akord skládá ze dvou polovin. Každý z nich je poloměr, který vyplývá z jeho definice jako segment, který spojuje bod na kruhu a jeho střed. Pokud je známý průměr problému, pak je třeba zjistit poloměr, který potřebujete k rozdělení této hodnoty o dvě. Vzorec je následující: R = D / 2. Například, je-li průměr v problému 10 m, pak je poloměr 5 metrů.

Podle oblasti kruhu

Tento typ úkolu se obvykle nazývá nejtěžší. To je způsobeno především nedostatečnou znalostí vzorce. Pokud víte, jak v tomto případě najít poloměr kruhu, pak je zbytek technickou záležitostí. V kalkulačce je třeba předem najít ikonu odmocniny. Plocha kruhu je součinem čísla P a poloměr je vynásoben samotným. Vzorec je následující: S = P * R ² . Oddělením poloměru na jedné straně rovnice můžete problém snadno vyřešit. Bude se rovnat druhá odmocnina z kvocientu plochy dělené číslem P. Pokud S = 10 m, pak R = 1,78 m. Stejně jako v předchozích úkolech je důležité nezapomínat na použité jednotky.

Jak zjistit poloměr obrysu

Předpokládejme, že a, b, c jsou strany trojúhelníku. Pokud znáte jejich hodnoty, pak najdete poloměr kružnice popsané kolem. Chcete-li to provést, musíte nejprve najít poloprůchod trojúhelníku. Chcete-li usnadnit čtení, označte jej malým písmem p. Bude se rovnat polovině částky stran. Jeho vzorec je: p = (a + b + c) / 2.

Také vypočítat produkt délky stran. Pro zjednodušení je označeno písmenem S. Vzorec pro poloměr ohraničené kružnice vypadá takto: R = S / (4 * √ (p * (p - a) * (p - b) * (p - c)).

Zvažte příklad úkolu. Máme kruh popisovaný kolem trojúhelníku. Délka jeho stran je 5, 6 a 7 cm. Nejprve vypočítáme poloprůchod. V našem problému se rovná 9 centimetrů. Teď vypočítáme produkt délky stran - 210. Nahradíme výsledky mezitímních výpočtů do vzorce a zjistíme výsledek. Poloměr ohraničeného kruhu je 3,57 centimetrů. Zaznamenáváme odpověď, aniž bychom zapomínali na měrné jednotky.

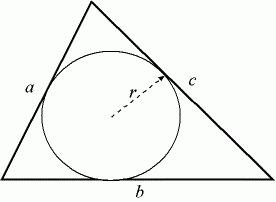
Jak najít poloměr zapsaného kruhu

Předpokládejme, že a, b, c jsou délky stran trojúhelníku. Pokud znáte jejich hodnoty, pak můžete najít poloměr kružnice, která je v nich zapsána. Nejprve musíte najít jeho poloprůchod. Pro snadnější porozumění je označujeme malým písmem p. Vzorec pro výpočet je následující: p = (a + b + c) / 2. Tento typ úkolu je poněkud jednodušší než předchozí, takže žádné další výpočty nejsou zapotřebí.

Poloměr zapsaného kruhu se vypočítá podle následujícího vzorce: R = √ ((p - a) * (p - b) * (p - c) / p). Zvažte to s konkrétním příkladem. Předpokládejme, že problém popisuje trojúhelník se stranami 5, 7 a 10 cm. V něm je vypsána kružnice, jejíž poloměr se nachází. Nejprve nalezneme poloprůchod. V našem problému se rovná 11 cm. Nyní ho nahrazujeme hlavním vzorcem. Poloměr bude rovný 1,65 centimetrů. Napsali jsme odpověď a nezapomněli na správné jednotky.

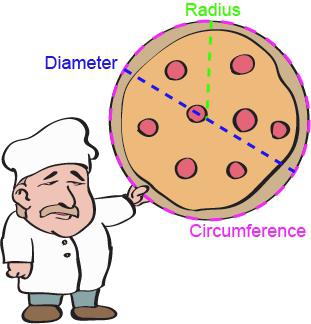
Kruh a jeho vlastnosti

Každý geometrický tvar má své vlastní vlastnosti. Z jejich pochopení závisí správnost řešení problémů. Mají kruh. Často se používají při řešení příkladů s popisy nebo popisy, protože dávají jasnou představu o této situaci. Mezi ně patří:

• Přímka může mít nulu, jeden nebo dva průsečíky s kruhem. V prvním případě se s ním netýká, ve druhé je tangentní, ve třetím - sekanci.
• Pokud vezmeme tři body, které nespočívají na jedné přímce, pak je možné vytvořit pouze jeden kruh.
• Přímou čarou může být tečna dvou čísel najednou. V tomto případě bude procházet bodem, který leží na segmentu, který spojuje středy kruhů. Jeho délka se rovná součtu poloměrů těchto čísel.
• Přes jeden nebo dva body můžete nakreslit nekonečný počet kruhů.