Logaritmy: pravidla, základní vlastnosti a vzorce

Logaritmy a pravidla jednání s nimi jsou poměrně prostorné a jednoduché. Proto pochopit toto téma nebude těžké. Jakmile se naučíte všechna pravidla přirozených logaritmů, problém se vyřeší nezávisle. První známost s tímto tématem se může zdát nudná a nesmyslná, ale pomocí logaritmů bylo řešeno mnoho problémů matematiků z 16. století. "Co to je?" - myslíš si. Přečtěte si článek nakonec a zjistěte, že tato část "Czariny věd" může být zajímavá nejen pro matematiky, vědce exaktních věd, ale i pro běžné studenty středních škol.

Definice logaritmu

Začněme definicí logaritmu. Jak říká mnoho učebnic: logaritmus čísla b na základě (log _a b) je určitý počet c, pro který platí tato rovnost: b = a ^c . Jednoduše řečeno, logaritmus je určitým stupněm, na který budeme vytvářet základnu pro získání daného čísla. Je však důležité si uvědomit, že logaritmus formu log _a b má smysl pouze tehdy, když: a> 0; a je číslo jiné než 1; b> 0, proto jsme dospěli k závěru, že logaritmus lze nalézt pouze pro kladná čísla.

Klasifikace logaritmu podle báze

Logaritmy mohou být libovolné kladné číslo na základně. Existují však také dva typy: přirozené a desítkové logaritmy.

• Přirozený logaritmus - logaritmus se základem e (e je Eulerovo číslo, číselně přibližně 2,7, iracionální číslo zavedené pro exponenciální funkci y = e ^x ) je označeno jako ln a = log _e a;
• Desetinný logaritmus je logaritmus se základnou 10, tj. Log ₁₀ a = lg a.

Základní pravidla logaritmů

Nejprve se musíte seznámit se základní logaritmickou identitou: ^{log _a b} = b, poté postupujte podle těchto dvou základních pravidel:

• log _a 1 = 0 - protože libovolné číslo v nulovém stupni je 1;
• log _a = 1.

Díky odhalení logaritmu není pro nás zcela obtížné řešit absolutně jakoukoli exponenciální rovnici, jejíž odpověď nemůže být vyjádřena v přirozených počtech, ale pouze iracionální. Například: 5 ^x = 9, x = log ₅ 9 (protože neexistuje přirozená x pro tuto rovnici).

Akce s logaritmy

• log _a (x · y) = log _a x + log _a y - pro nalezení logaritmu produktu je třeba přidat logaritmy faktorů. Všimněte si, že základy logaritmu jsou stejné. Pokud to napíšeme v opačném pořadí, získáme pravidlo přidání logaritmu.
• log _a xy = log _a x - log _a y - pro nalezení logaritmu konkrétního, musíte najít rozdíl mezi logaritmy dividendy a dělitele. Poznámka: logaritmy mají stejnou základnu. Při psaní v opačném pořadí získáváme pravidlo odčítání logaritmů.

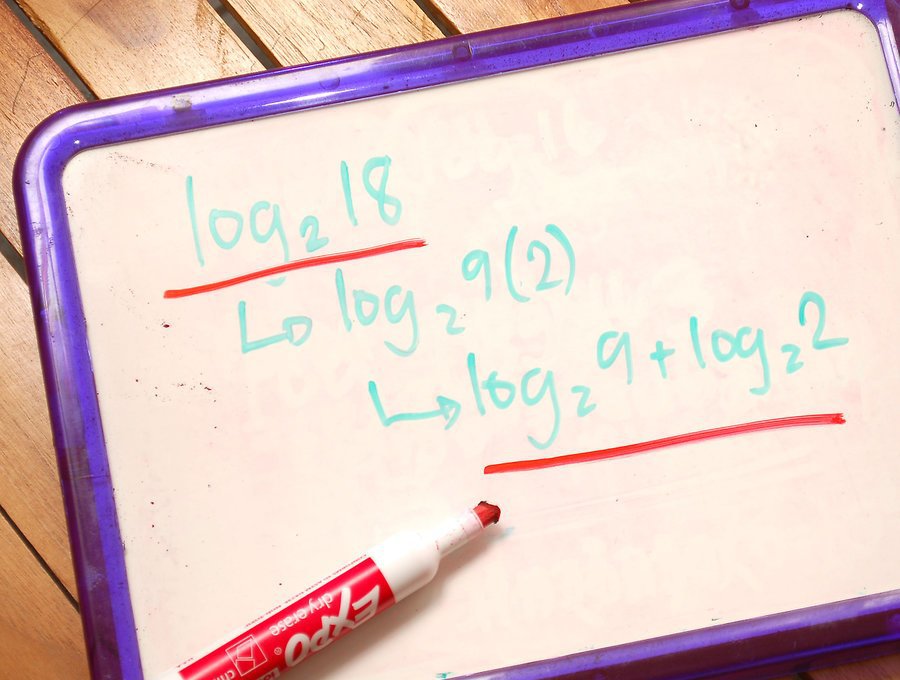
• log _{a ^k} x ^p = (p / k) * log _a x - tedy pokud jsou v argumentu a v základu logaritmu stupně, mohou být odebrány z logaritmu.
• log _a x = log _{a ^c} x ^c je zvláštní případ předchozího pravidla, když jsou exponenti rovni, mohou být redukováni.
• log _a x = (log _b x) (log _b a) je tzv. přechodový modul, postup konverze logaritmu na jiný základ.
• log _a x = 1 / log _x a je zvláštní případ přechodu, změny míst základny a daného čísla. Celý výraz, obrazně řečeno, se otočí a logaritmus s novou základnou se objeví v jmenovateli.

Historie logaritmu

V 16. století bylo nutné provést řadu přibližných výpočtů pro řešení praktických problémů, zejména v astronomii (například určení polohy lodě sluncem nebo hvězdami).

Tato potřeba rostla rychle a značné obtíže vedly k násobení a rozdělení vícedístných čísel. A matematický matematik Napier se rozhodl nahradit násobení intenzivní práce za obyčejný přírůstek pro trigonometrické výpočty, což porovnává určité pokroky. Pak se dělení podobně nahrazuje jednodušším a spolehlivějším postupem - odčítání a pro extrahování kořenu n-stupně je nutné rozdělit logaritmus radikandu o n. Řešení tak obtížného úkolu v matematice jasně odráží cíle Napera ve vědě. Zde je, jak o tom napsal na začátku své knihy Rabdologiya:

Vždycky jsem se snažil, pokud moje síly a schopnosti dovolily, osvobodit lidi od potíží a nudy výpočtů, jejichž obtěžování obvykle dělá velmi mnoho lidí od studování matematiky.

Jméno logaritmus navrhl sám Napier, získal se kombinací řeckých slov, které v kombinaci znamenaly "počet vztahů".

Základ logaritmu byl představen společností Spadel. Zapůjčil Euulera z teorie stupňů a přenesl se do teorie logaritmu. Koncept logaritmu se stal známým díky Koppovi v 19. století. Použití přírodních a dekadických logaritmů, stejně jako jejich označení, se objevilo díky Cauchymu.

V roce 1614 vydal John Napier v latině esej "Popis úžasné tabulky logaritmů". Byl zde stručný popis logaritmů, pravidel a jejich vlastností. Takže termín "logaritmus" byl založen v přesných vědách.

Logaritmická operace a první zmínka o ní se objevila díky Wallisovi a Johandu Bernoullimu a konečně ji založil Euler ve století XVIII.

Eulerova zásluha je rozšíření logaritmické funkce formy y = log _a x na komplexní doménu. V první polovině 18. století byla publikována jeho kniha "Úvod do analýzy nekonečna", ve které existovaly moderní definice exponenciálních a logaritmických funkcí.

Logaritmická funkce

(имеет смысл, только если: а > 0, а ≠ 1). Funkce tvaru y = log _a x (má smysl pouze pokud: a> 0, a ≠ 1).

• Logaritmická funkce je určena množinou všech pozitivních čísel, jelikož záznamový záznam _a x existuje pouze za podmínky - x> 0;
• Tato funkce může mít absolutně všechny hodnoty ze sady R (reálná čísla). Vzhledem k tomu, že každé reálné číslo b má pozitivní x, aby uspokojilo protokol _o rovnosti _a x = b, to znamená, že tato rovnice má kořen - x = a ^b (vyplývá z toho, že log _a a ^b = b).
• Funkce se zvyšuje o interval a> 0 a snižuje interval 0 <a <1.
• Je-li a> 0, potom funkce přebírá kladné hodnoty pro x> 1.

Je třeba si uvědomit, že všechny grafy logaritmické funkce y = log _a x mají jeden stacionární bod (1; 0), protože log _a 1 = 0. To je jasně vidět na obrázku níže.

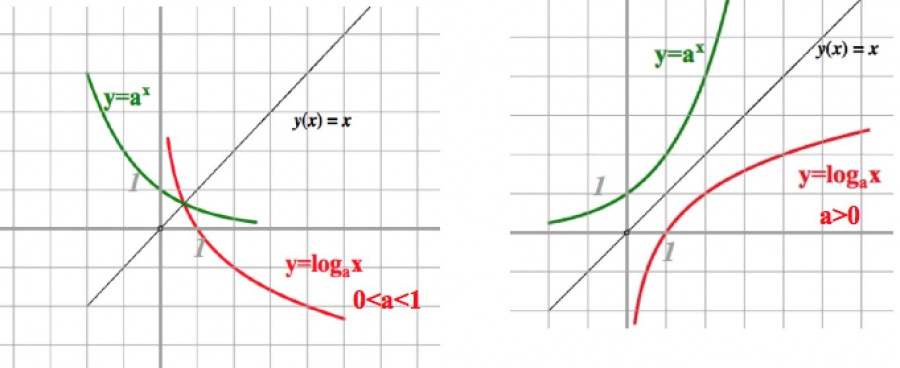
Jak vidíme na obrázcích, funkce nemá rovnoměrnost nebo zvláštnost, nemá největší nebo nejmenší hodnoty, není omezena shora ani níže.

Logaritmická funkce y = log _a x a exponenciální funkce y = a ^x , kde (a> 0 a ≠ 1) jsou navzájem inverzní. To lze vidět na obrázku jejich grafů.

Řešení problémů s logaritmy

Obvykle řešení problému obsahujícího logaritmy je založeno na jejich konverzi na standardní formulář nebo je zaměřeno na zjednodušení výrazů pod znaménkem logaritmu. Nebo je nutné překládat obvyklé přirozená čísla na logaritmy s nezbytným základem pro provedení dalších operací s cílem zjednodušit výraz.

Existují některé jemnosti, které bychom neměli zapomenout:

• Při řešení nerovností, kdy obě části stojí podle logaritmu podle pravidla s jednou základnou, nesdělej spěchat "zrušit" znak logaritmu. Nezapomeňte na monotónní intervaly logaritmické funkce. Protože pokud je základna větší než 1 (případ, kdy se funkce zvyšuje) - znak nerovnosti zůstává nezměněn, ale když je základna větší než 0 a menší než 1 (případ, kdy funkce klesá) - značka nerovnosti se změní naopak;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Nezapomeňte na definici logaritmu: log _a x = b, a> 0 a ≠ 1 a x> 0, aby nedošlo ke ztrátě kořenů kvůli nezaznamenanému rozsahu platných hodnot. Rozsah TLD (přípustný rozsah hodnot) existuje téměř pro všechny složité funkce.

Při řešení logaritmických rovnic se doporučuje použít ekvivalentní transformace. Také musíte být opatrní a brát v úvahu možné transformace, které mohou vést ke ztrátě některých kořenů.

Jedná se o obvyklé, ale velké chyby, které se mnozí setkali při hledání správné odpovědi na úkol. Neexistuje mnoho pravidel pro řešení logaritmů, takže toto téma je jednodušší než jiné a následující, ale mělo by být dobře pochopeno.

Závěr

Toto téma se může na první pohled zdát komplikované a těžkopádné, ale hlouběji a hlouběji je poznáte, že začnete chápat, že téma právě skončilo a potíže nezpůsobily nic. Zkontrolovali jsme všechny vlastnosti, pravidla a dokonce i chyby související s tématem logaritmu. Úspěchy v učení!