Matematická analýza a její role v moderním světě

Dějiny

Filozofie se považuje za zaměření všech věd, protože zahrnuje první zárodky literatury, astronomie, literatury, přírodních věd, matematiky a dalších oblastí. Časem se každá oblast vyvinula nezávisle, matematika nebyla výjimkou. První "náznak" analýzy je považován za teorii rozkladu do nekonečně malých hodnot, ke kterému se mnozí mysli snažili přiblížit, ale měli mlhavou povahu a neměli žádný základ. Je to důsledkem připoutání ke staré škole vědy, která byla přísně formulována. Isaac Newton byl velmi blízko k vytvoření základny, ale pozdě. V důsledku toho je jeho vzhled jako samostatný systém matematické analýzy povinen filozofovi Gottfriedovi Leibnizovi. Byl to ten, kdo v pracích předkládaných vědeckému světu takové pojmy, minimálně a maximálně, inflexní a konvexní funkční graf formulovaly základy diferenciálního počtu. Od tohoto okamžiku je matematika oficiálně rozdělena na elementární a vyšší.

Matematická analýza. Naše dny

Jakákoli odbornost, ať již technická nebo humanitární, zahrnuje analýzu v průběhu studia. Hloubka studia se liší, ale podstata zůstává stejná. Přes veškerou "abstraktnost" je jedním z pilířů, na nichž spočívá přírodní věda ve svém moderním pojetí. S jeho pomocí byla vyvinuta fyzika a ekonomika, je schopen popsat a předvídat činnosti burzy, aby pomohl vybudovat optimální portfolio akcií. Úvod do matematické analýzy je založen na základních pojmech:

• sady;
• základní operace sady;
• vlastnosti operací na sadách;
• funkce (jinak mapování);
• typy funkcí;
• sekvence;
• číselné čáry;
• sekvenční limit;
• vlastnosti mezních hodnot;
• funkce kontinuity.

Stojí za to izolovat takové pojmy jako množina, bod, čára, rovina odděleně. Všechny z nich nemají žádné definice, neboť jsou základními pojmy, na kterých je postavena veškerá matematika. Všechno, co lze v procesu práce udělat, je vysvětlit, co přesně v jednotlivých případech znamená.

Omezit jako pokračování

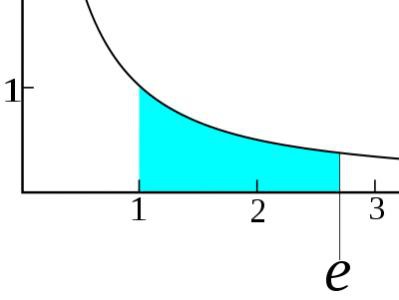Základem matematické analýzy je limit. V praxi je to hodnota, ke které má tendence sekvence nebo funkce, přichází tak blízko, jak si přeje, ale nedosáhne. Označuje to lim, považujeme za zvláštní případ limitu funkce: lim (x-1) = 0 jako x → 1. Z tohoto nejjednoduššího příkladu je zřejmé, že jako x → 1, celá funkce má tendenci 0, protože pokud nahradíme limit do samotné funkce, dostaneme (1-1) = 0. Podrobněji, od elementárních až po komplikované konkrétní případy, jsou informace prezentovány v jakési analýze "Bible" - díla Fichtenholze. Zde se v kontextu matematické analýzy, hranic, jejich odvozování a dalšího uplatnění uvažuje. Například odvození čísla e (Eulerova konstanta) by bez teorie limitů nebylo možné. Přes dynamickou abstraktnost teorie se limity aktivně využívají v praxi ve stejné ekonomice a sociologii. Například s tím nemůžeme dělat, když účtujeme úroky z bankovního vkladu.