Mechanický pohyb ve fyzice

Co je mechanické hnutí a jak to charakterizuje? Jaké parametry jsou zavedeny pro pochopení tohoto typu pohybu? Které pojmy současně nejčastěji fungují? V tomto článku zodpovíme tyto otázky, zvážíme mechanické pohyby z různých úhlů pohledu, ukážeme příklady a řešíme problémy z fyziky příslušného předmětu.

Základní pojmy

Dokonce i ve škole se učíme, že mechanický pohyb je změnou polohy těla kdykoli ve vztahu k jiným tělům systému. Ve skutečnosti je to všechno. Vezměme si obyčejný dům, v němž jsme, pro nulový souřadnicový systém. Představte si vizuálně, že dům bude původem souřadnic a osa úsečky a osa osy budou z něj vycházet ve všech směrech.

V tomto případě bude náš pohyb uvnitř domova a mimo něj jasně demonstrovat mechanický pohyb těla v referenčním rámci. Představte si, že se bod pohybuje podél souřadnicového systému a v každém okamžiku mění svou souřadnici vzhledem k ose x i k ose y. Všechno bude jednoduché a jasné.

Charakteristika mechanického pohybu

Jaký by mohl být tento typ pohybu? Nebudeme jít hluboko do divočiny fyziky. Zvažte nejjednodušší případy, kdy dochází k pohybu hmotného bodu. Je rozdělen na přímočarý pohyb a křivočarý pohyb. V zásadě by mělo být z titulu jasné, ale hovoříme o tom konkrétněji jen pro případ.

Přímý pohyb materiální bod bude nazýván takový pohyb, který se provádí po trajektorii a má tvar přímky. Například auto jde přímo pod silnici, která nemá žádné otáčky. Nebo na místě podobné cesty. Bude to přímý pohyb. V tomto případě může být rovnoměrně nebo jednotně zrychlena.

Křivočasový pohyb materiálu bodu se nazývá takový pohyb, který se provádí po trajektorii, která nemá tvar přímky. Trajektorií může být přerušovaná čára, stejně jako uzavřená čára. To je kruhová cesta, elipsoid a tak dále.

Mechanický pohyb obyvatelstva

Tento druh pohybu nemá téměř nic společného s fyzikou. I když podle toho, co ho vnímáme. Co se obecně nazývá mechanickým pohybem obyvatelstva? Jsou nazývány přemísťováním jednotlivců, ke kterým dochází v důsledku migračních procesů. Může to být jak vnější, tak vnitřní migrace. Trvání mechanického pohybu populace je rozděleno na trvalé a dočasné (plus kyvadlo a sezónní).

Pokud tento proces z fyzického pohledu považujeme, můžeme jen říci jednu věc: toto hnutí dokáže dokonale prokázat pohyb hmotných bodů v referenčním systému spojeném s naší planetu - Zemí.

Jednotný mechanický pohyb

Jak naznačuje název, jedná se o typ pohybu, ve kterém má rychlost těla určitou hodnotu, která je v absolutní hodnotě udržována konstantní. Jinými slovy, rychlost těla, která se pohybuje rovnoměrně, se nemění. V reálném životě si můžeme sotva všimnout dokonalých příkladů jednotného mechanického pohybu. Můžete se zcela rozumně domnívat, říkají, že můžete jet autem rychlostí 60 km / h. Samozřejmě, rychloměrný vůz může prokázat podobnou hodnotu, ale to neznamená, že ve skutečnosti bude rychlost auta přesně šedesát kilometrů za hodinu.

O čem to mluvíme? Jak víme, nejprve vše měřicí přístroje mít určitou chybu. Pravítka, váhy, mechanická a elektronická zařízení - všichni mají určitou chybu, nepřesnost. Můžete si pro sebe uvědomit, že si užíváte tucet řádků a používáte je jeden k druhému. Poté si budete moci všimnout některých nesrovnalostí mezi milimetrovými značkami a jejich použitím.

Totéž platí pro rychloměr. Má určitou chybu. U nástrojů je nepřesnost číselně rovna polovině ceny dělení. V autě bude nepřesnost rychloměru 10 kilometrů za hodinu. Proto v určitém okamžiku nelze s jistotou říci, že se pohybujeme jednou rychlostí nebo jinou cestou. Druhým faktorem, který přispěje k nepřesnosti, budou síly působící na automobil. Ale síly jsou neoddělitelně spojeny s akcelerací, takže o tomto tématu budeme hovořit později.

Velmi často se objevuje rovnoměrný pohyb v problémech matematické povahy spíše než fyzických. Tam se motocyklisté, nákladní automobily a automobily pohybují stejnou rychlostí, která se v různých časových okamžicích rovná jejich velikosti.

Rovnoměrně zrychlený pohyb

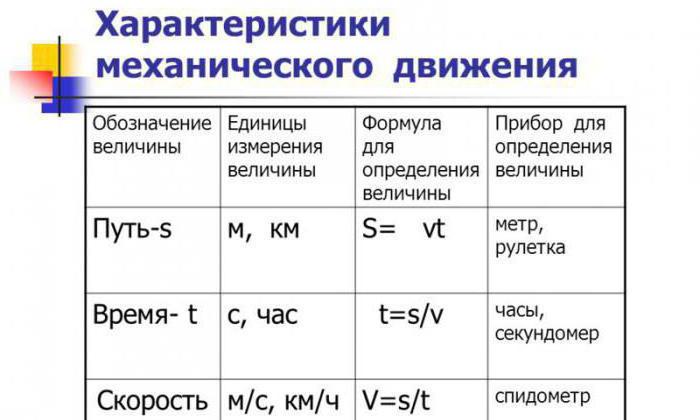
Ve fyzice se tento typ pohybu objevuje poměrně často. Dokonce i v úkolech části "A" v 9. a 11. třídě existují úkoly, v nichž musíte být schopni provádět operace s akcelerací. Například "A-1", kde je nakreslený graf pohybu tělesa v souřadnicových osách a je třeba vypočítat, jak daleko vozidlo prošlo během daného časového období. Navíc jeden z intervalů může prokázat jednotný pohyb, zatímco na druhém je nutné nejprve vypočítat zrychlení a teprve poté vypočítat ujetou vzdálenost.

Jak to víš? je pohyb jednotně zrychlen? Obvykle v případě problémů se informace o této skutečnosti podávají přímo. To znamená, že je zde buď číselná indikace zrychlení, nebo parametry (čas, změna rychlosti, vzdálenost), které nám umožňují určit zrychlení. Mělo by být poznamenáno, že zrychlení je vektorové množství. Takže to může být nejen pozitivní, ale i negativní. V prvním případě pozorujeme zrychlení těla, v druhém - jeho inhibici.

Stává se však, že informace o typu hnutí jsou vyučovány studentovi v poněkud utajené podobě, pokud mu to můžete nazvat. Říká se například, že na těle nic nekoná, nebo součet všech sil je nulový. No, v tomto případě musíte jasně pochopit, že hovoříme o jednotném pohybu nebo zbytku těla v určitém souřadném systému. Pokud si vzpomenete na druhý zákon Newtona (který říká, že součet všech sil není nic jiného než produkt tělesné hmoty a zrychlení, ohlásený akcí odpovídajících sil), snadno si všimnete jednu zajímavou věc: pokud součet síly je nulový, pak produkt hmotnosti a zrychlení bude také nulový.

Závěr

Ale koneckonců hmotnost je naší konstantní hodnotou a nemůže být a priori nulová. V tomto případě by bylo logické dospět k závěru, že při neexistenci vnějších sil (nebo když jsou kompenzovány touto činností) nedochází k zrychlení těla. To znamená, že buď spočívá nebo se pohybuje konstantní rychlostí.

Stejně zrychlený vzorec

Někdy ve vědecké literatuře existuje přístup, podle něhož jsou nejprve uvedeny vzorce světla, a pak se s ohledem na určité faktory stávají komplikovanějšími. Uděláme opak, jmenovitě budeme nejprve zvažovat jednotně zrychlený pohyb. Vzorec, podle kterého se ujetá vzdálenost vypočte takto: S = V0t + při ^ 2/2. Zde V0 je počáteční rychlost těla, a je zrychlení (možná negativní, pak se změní znaménko + ve vzorci) a t je čas, který uplynul od začátku pohybu až po zastavení těla.

Jednotný pohybový vzorec

Když hovoříme o jednotném pohybu, pak si připomínáme, že v tomto případě je zrychlení nula (a = 0). Nahraďte nulou ve vzorci a dostaneme: S = V0t. Ale koneckonců, rychlost v celé části cesty je konstantní, pokud hovoříme hrubě, to znamená, že musíme zanedbávat síly působící na tělo. Což je mimochodem praktikováno všude v kinematiku, protože kinematika nezajímá příčiny pohybu, to je to, co dělá dynamika. Takže pokud je rychlost po celé části cesty konstantní, pak se její počáteční hodnota shoduje s jakýmkoli mezilehlým a konečným výsledkem. Proto vzorec vzdálenosti bude vypadat takto: S = Vt. To je všechno.