Moment setrvačnosti: vzorec. Moment setrvačnosti těla

Chcete-li změnit rychlost pohybu tělesa v prostoru, je třeba vyvinout určité úsilí. Tato skutečnost platí pro všechny typy mechanického pohybu a je spojena s přítomností inerciálních vlastností objektů majících hmotnost. Tento článek pojednává o rotaci těl a uvádí koncept jejich momentu setrvačnosti.

Co je rotace z hlediska fyziky?

Odpověď na tuto otázku může dát všem, protože tento fyzický proces se nijak neliší od jeho koncepce v každodenním životě. Proces rotace je pohyb objektu s konečnou hmotností podél kruhové dráhy kolem nějaké imaginární osy. Následující příklady rotace mohou být uvedeny:

• Pohyb kol u auta nebo na kole.
• Otáčení lopatek vrtulníku nebo ventilátoru.
• Pohyb naší planety kolem osy a kolem slunce.

Jaké fyzikální veličiny charakterizují proces rotace?

Kruhový pohyb je popsán množinou veličin ve fyzice, z nichž hlavní jsou uvedeny níže:

• r je vzdálenost k ose hmotného bodu hmoty m.
• ω a α jsou úhlová rychlost a zrychlení. První hodnota ukazuje, kolik radiánů (stupňů) tělo rotuje kolem osy za jednu sekundu, druhá hodnota popisuje rychlost změny v čase první.
• L je moment hybnosti, který se podobá podobnému charakteru v lineárním pohybu.
• I - okamžik setrvačnosti těla. Tato hodnota je podrobněji popsána níže.
• M je okamžik síly. Charakterizuje stupeň změny hodnoty L, pokud je použita vnější síla.

Tato množství jsou navzájem spojena těmito vzorci rotačního pohybu:

1. L = I * ω

2. M = I * α

První vzorec popisuje kruhový pohyb těla v nepřítomnosti působení vnějších momentů sil. Ve výše uvedené podobě odráží zákon zachování momentu hybnosti L. Druhý výraz popisuje případ zrychlení nebo zpomalení otáčení těla v důsledku působení momentu síly M. Obě výrazy se často používají k řešení problémů dynamiky po kruhové cestě.

Jak je zřejmé z těchto vzorců, moment setrvačnosti kolem osy (I) v nich je použit jako určitý koeficient. Zvažme tuto hodnotu podrobněji.

Odkud pochází hodnota?

V této sekci považujeme nejjednodušší příklad rotace: kruhový pohyb hmotného bodu hmoty m, jehož vzdálenost od osy otáčení je r. Tato situace je znázorněna na obrázku.

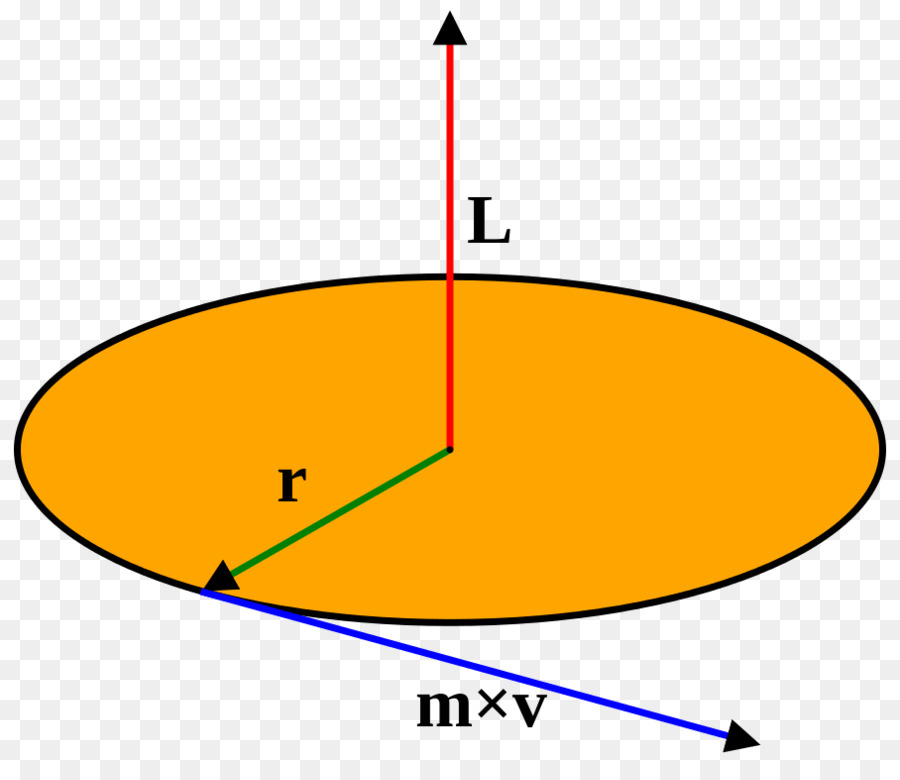
Podle definice je úhlová hybnost L zapsána jako součin ramena r lineárními impulsními body p:

L = r * p = r * m * v, protože p = m * v

Vzhledem k tomu, že lineární a úhlová rychlost jsou navzájem spojena vzdáleností r, může být tato rovnost přepsána jako:

v = ω * r => L = m * r ² * ω

Produkt hmoty materiálu bodu čtvercem vzdálenosti k ose otáčení se nazývá moment setrvačnosti. Výše uvedený vzorec bude v tomto případě přepsán následovně:

I = m * r ² => L = I * ω

To znamená, že jsme dostali výraz, který byl uveden v předchozím odstavci, a představil hodnotu I.

Obecný vzorec pro velikost těla I

Výraz momentu setrvačnosti s hmotností m materiálu je základní, to znamená, že umožňuje vypočítat tuto hodnotu pro libovolné těleso mající libovolný tvar a nerovnoměrné rozložení hmoty v něm. K tomu je třeba rozdělit předmět, který je předmětem úvahy, na malé elementy hmoty m _i (celé číslo i je číslo prvku), pak je vynásobte čtvercem vzdálenosti r _i ² k ose, kolem které se zvažuje rotace, a přidejte výsledky. Popsaný způsob nalezení hodnoty I může být napsán matematicky následujícím způsobem:

I = Σ _i (m _i * r _i ² )

Pokud je tělo rozdělen tak, že i-> ∞, pak je daná část nahrazena integrální hodnotou nad hmotností tělesa m:

I = ∫ _m (r _i ² * dm)

Tento integrál je ekvivalentní k jinému integrálnímu na objemu tělesa V, protože dV = ρ * dm:

I = ρ * ∫ _V (r _i ² * dV)

Všechny tři vzorce se používají k výpočtu momentu setrvačnosti těla. V tomto případě je v případě diskrétní distribuce hmoty v systému výhodnější použít první výraz. S kontinuálním rozdělením hmotnosti použijte třetí výraz.

Vlastnosti I a jeho fyzický význam

Popsaný postup pro získání obecného výrazu pro I nám dovoluje vyvodit některé závěry o vlastnostech tohoto fyzického množství:

• je aditivní, to znamená, že celkový moment setrvačnosti systému může být reprezentován jako součet momentů jeho jednotlivých částí;
• záleží na rozložení hmotnosti uvnitř systému, stejně jako na vzdálenosti k ose otáčení, čím větší je, tím větší je I;
• to nezávisí na sílách M, které působí na systém momentů a na otáčkách ω.

Fyzický význam I je, jak silně systém zabraňuje jakékoliv změně rychlosti otáčení, tj. Moment setrvačnosti charakterizuje stupeň "hladkosti" výsledných zrychlení. Například kolečko pro jízdní kolo lze snadno otáčet až na vysoké úhlové rychlosti a je také snadné jej zastavit, ale pro změnu otáčení setrvačníku na klikovém hřídeli automobilu to bude vyžadovat značné úsilí a určitý čas. V prvním případě existuje systém s malým momentem setrvačnosti, ve druhém - s velkým momentem setrvačnosti.

Hodnota I některých těles pro osu rotace procházející středem hmoty

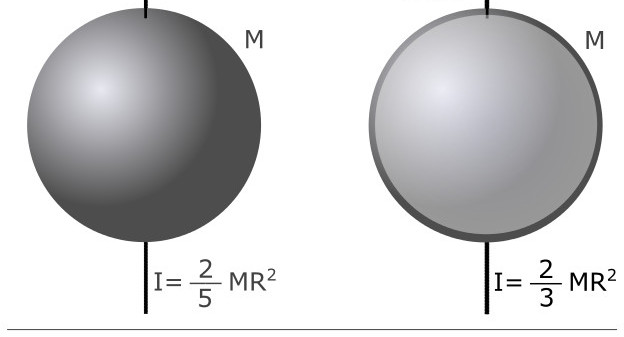
Použijeme-li integraci nad objem pro všechna těla s libovolným rozložením hmoty, pak můžeme získat množství I. Pro homogenní objekty, které mají ideální geometrický tvar, byl tento problém již vyřešen. Vzorce momentu setrvačnosti pro tyč, kotouč a kuličku s hmotností m, ve kterých je jejich základní složka rovnoměrně rozdělena, jsou uvedeny níže:

• Jádro. Osa otáčení běží kolmo k ní. I = m * L 2/12, kde L je délka tyče.
• Disk libovolné tloušťky. Moment setrvačnosti s osou otáčení, která prochází kolmo k její rovině středem hmotnosti, se vypočte takto: I = m * R 2/2, kde R je poloměr disku.
• Ples. Vzhledem k vysoké symetrii tohoto obrázku pro libovolnou polohu osy procházející středem I = 2/5 * m * R2, zde R je poloměr koule.

Níže uvádíme dva příklady řešení problémů pro uplatnění obecného vzorce pro výpočet I a pro použití vlastnosti aditivity tohoto množství.

Úloha výpočtu hodnoty I pro systém s diskrétním rozdělením hmotnosti

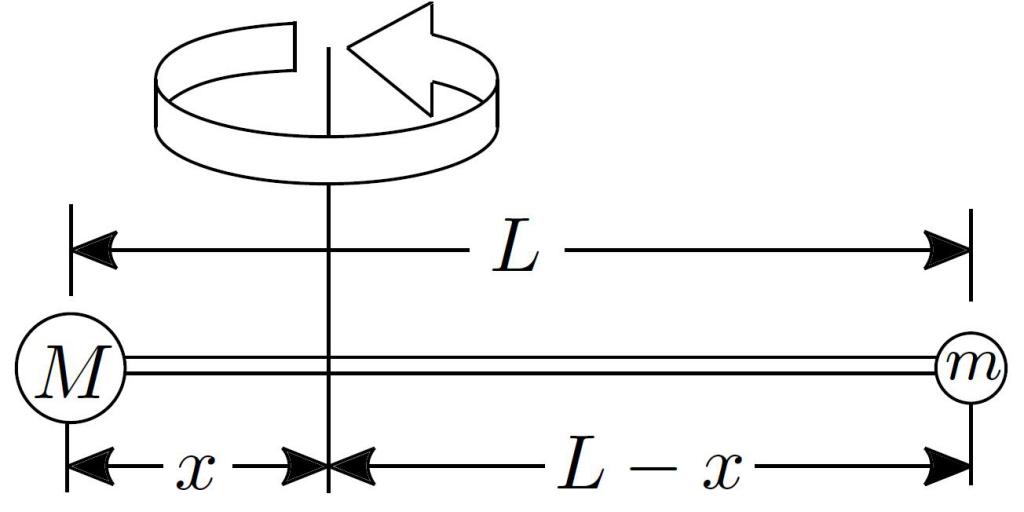
Představte si tyč o délce 0,5 metru, která je vyrobena z tvrdého a lehkého materiálu. Tato tyč je upevněna na ose tak, že se pohybuje kolmo k ní přesně uprostřed. Na této tyči jsou zavěšena tři závaží: na jedné straně nápravy jsou dvě závaží o hmotnosti 2 kg a 3 kg, umístěné ve vzdálenosti 10 cm a 20 cm od jejího konce; na druhé straně je na konec tyče zavěšena jedna hmotnost 1,5 kg. Pro tento systém je nutné vypočítat moment setrvačnosti I a určit, jakou rychlost ot otáčí tyč, je-li síla 50 N aplikována na jeden ze svých konců po dobu 10 sekund.

Vzhledem k tomu, že hmotnost tyče může být zanedbatelná, je nutné vypočítat okamžik I pro každé zatížení a přidat získané výsledky k získání celého okamžiku systému. Podle stavu úlohy je z osy hmotnost 2 kg ve vzdálenosti 0,15 m (0,25-0,1), zatížení 3 kg je 0,05 m (0,25-0,20), zatížení 1,5 kg je 0,25 m. Pomocí vzorce pro okamžik bodu I materiálu získáme:

I = I ₁ + I ₂ + I ₃ = m ₁ * r ₁ ² + m ₂ * r ₂ ² + m ₃ * r ₃ ² = 2 * (0.15) ² + 1,5 * (0,25) ² = 0,14 625 kg * m ² .

Mějte na paměti, že při výpočtech byly všechny jednotky měření přeneseny do systému SI.

K určení úhlové rychlosti otáčení tyče po působení síly byste měli použít vzorec s okamžikem síly, který byl uveden v druhém odstavci článku:

M = I * α

Protože α = Δω / Δt a M = r * F, kde r je délka ramene, dostaneme:

r * F = I * Δo / Δt => Δω = r * F * Δt / I

Vzhledem k tomu, že r = 0,25 m, nahrazujeme čísla ve vzorci, dostaneme:

Δi = r * F * Δt / I = 0,25 * 50 * 10 / 0,14625 = 854,7 rad / s

Výsledná hodnota je poměrně velká. Chcete-li dosáhnout obvyklé rychlosti, měli byste rozdělit Δω o 2 * pi radiány:

f = Dor / (2 x pi) = 854,7 / (2 * 3,1416) = 136 s- ¹

Přiložená síla F na konec tyče s váhami za 10 sekund bude točit na frekvenci 136 otáček za sekundu.

Výpočet hodnoty I pro tyč, když os prochází jeho koncem

Nechť existuje homogenní tyč s hmotností m a délkou L. Je třeba určit moment setrvačnosti, pokud je osa otáčení umístěna na konci tyče kolmo k ní.

Používáme obecný výraz pro I:

I = ρ * ∫ _V (r _i ² * dV)

Při rozložení předmětu do elementárních objemů si všimneme, že dV může být napsán jako dr * S, kde S je řezná plocha lišty a dr je tloušťka štípacího prvku. Nahrazením tohoto výrazu do vzorce máme:

I = ρ * S * ∫ _L (r ² * dr)

Tento integrál je poměrně jednoduchý k výpočtu, získáváme:

I = ρ * S * (r 3/3) | ₀ ^L => I = ρ * S * L 3/3

Jelikož objem tyče je S * L a hmotnost je ρ * S * L, dostaneme konečný vzorec:

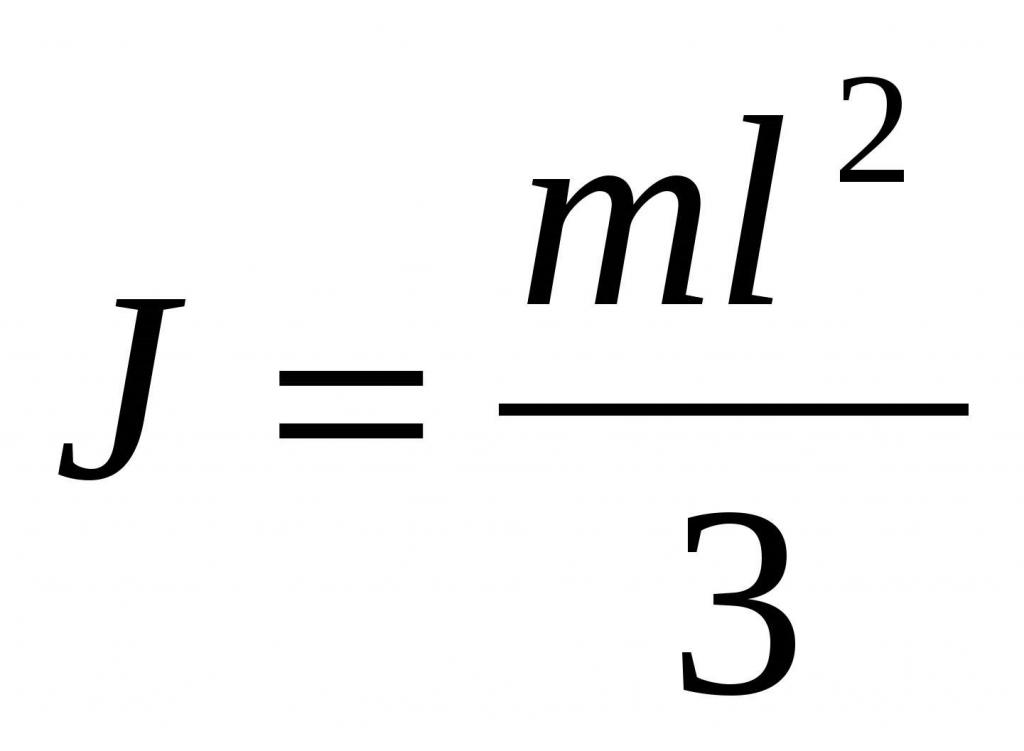
Je zajímavé poznamenat, že moment setrvačnosti pro stejný prut, když os prochází jeho středem hmotnosti, je 4krát menší než získaná hodnota (m * L 2/3 / (m * L 2/12) = 4).