Rovnoběžnost rovin: znamení, podmínka

Každý, kdo někdy studoval nebo v současné době studuje ve škole, musel čelit různým obtížím při studiu disciplín, které jsou součástí programu vyvinutého ministerstvem školství.

Jaké potíže musí čelit

Jazyky učení jsou doprovázeny memorováním stávajících gramatických pravidel a hlavních výjimek z nich. Tělesná výchova vyžaduje velké množství výpočtů, fyzickou zdatnost a velkou trpělivost ze strany studentů.

Nicméně nelze srovnávat s problémy, které vznikají při studiu přesných disciplín. Algebra obsahuje složité způsoby řešení základních problémů. Fyzika s bohatou sadou fyzikálních zákonů. Geometrie a její části, které jsou založeny na komplexních větách a axiomech.

Příkladem by byly axiomy vysvětlující teorii rovnoběžnosti mezi letadly, která musí být nutně zapamatována, neboť jsou základem celého kurzu učebního plánu ve stereometrii. Pokusíme se zjistit, jak je to jednodušší a rychlejší.

Paralelní roviny podle příkladů

Axiom, který ukazuje rovnoběžnost rovin, zní takto: " Jakékoliv dvě roviny jsou považovány za paralelní pouze tehdy, pokud neobsahují společné body ", to znamená, že se navzájem nepřetvářejí. Abychom si představili tento obrázek podrobněji, jako základní příklad můžeme dát poměr stropu a podlahy nebo protilehlých zdí v budově. Stane se okamžitě jasné, co se myslí, a také potvrzuje skutečnost, že v obvyklém případě se tyto letadla nikdy nebudou protínat.

Dalším příkladem je jednotka skleněného skla, kde skleněné tkaniny působí jako letadla. Také za žádných okolností nebudou vytvářet průsečíky. Kromě toho můžete přidat knihovny, Rubikovu kostku, kde jsou letadla opačnými stranami a další prvky každodenního života.

Dané letadla jsou označena zvláštním označením ve tvaru dvou přímých čar "||", které jasně ilustrují rovnoběžnost rovin. Použitím skutečných příkladů lze vytvořit jasnější vnímání tématu a v důsledku toho lze pokračovat v posuzování složitějších pojmů.

Kde a jak se používá teorie rovnoběžných rovin?

Při studiu na kurzu geometrie se studenti potýkají s mnohastrannými problémy, kde je často nutné určit vzájemnou rovnoběžnost linií, linií a rovin mezi sebou nebo vzájemnou závislost letadel. Při analýze stávajícího stavu lze každý úkol souviset se čtyřmi hlavními třídami stereometrie.

První třída zahrnuje úkoly, ve kterých je nutné určit rovnoběžnost linie a roviny mezi sebou. Její řešení snižuje dokázání věty se stejným názvem. K tomu je třeba určit, zda v této rovině leží rovnoběžná přímka pro přímku, která nepatří do příslušné roviny.

Druhá skupina úkolů zahrnuje ty, ve kterých se jedná o rys paralelnosti rovin. Používá se k zjednodušení důkazního procesu, čímž se významně snižuje doba hledání řešení.

Další třída pokrývá řadu problémů souladů s přímými základními vlastnostmi rovnoběžnosti rovin. Řešení problémů čtvrté třídy spočívá v určení, zda je splněna podmínka rovnoběžnosti rovin. Vědět přesně, jak se objevuje důkaz o konkrétním problému, je pro studenty snazší orientovat se při použití jejich existujícího arzenálu geometrických axiomů.

Úlohy, jejichž stav vyžaduje vymezení a prokázání rovnoběžnosti přímky, přímky a roviny nebo dvou rovin mezi sebou, jsou omezeny na správný výběr věty a řešení podle stávajícího souboru pravidel.

O paralelnosti linie a roviny

Paralelismus přímky a roviny je zvláštní téma ve stereometrii, protože to je základní koncept, na kterém jsou založeny všechny následující vlastnosti paralelismus geometrických obrazců.

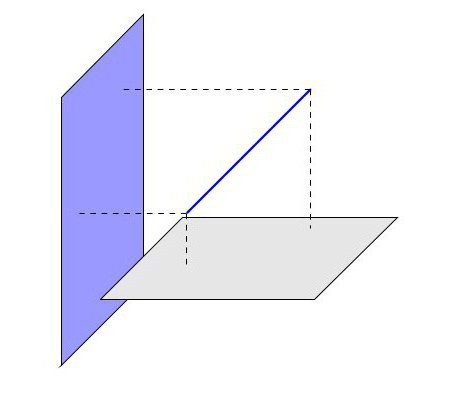
Podle existujících axiomů, v případě, že dva body přímky patří do určité roviny, můžeme usoudit, že tato rovná čára leží také v ní. V této situaci je zřejmé, že existují tři možnosti pro umístění přímky vzhledem k rovině ve vesmíru:

1. Linka patří rovině.
2. Pro přímku a rovinu existuje jeden společný průsečík.
3. Pro přímku a rovinu nejsou průsečíky chybí.

Zejména jsme se zajímali o druhou možnost, pokud neexistují průsečíky. Pouze pak můžeme říci, že přímka a rovina vůči sobě jsou paralelní. Proto je potvrzena podmínka hlavní věty na paralelním znaménku přímky a roviny, která říká, že: "Jestliže přímka, která nepatří do dotyčné roviny, je rovnoběžná s libovolnou přímkou ​​v této rovině, přímka je rovnoběžná s danou rovinou".

Potřeba použít funkci paralelního uspořádání

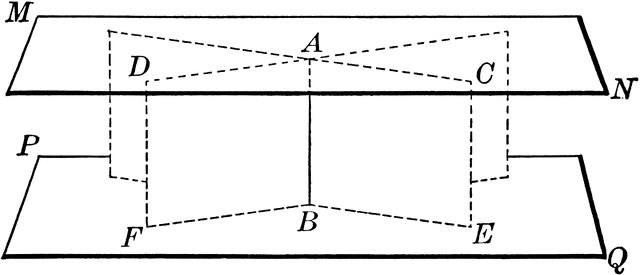
Značka rovnoběžnosti letounů se zpravidla používá k hledání zjednodušeného řešení problémů s letadly. Podstata této funkce je následující: " Jsou-li dvě rovnoběžné přímky ležící v jedné rovině, rovnoběžné s dvěma rovnými čarami náležejícími k jiné rovině, mohou být tyto roviny nazývány rovnoběžně ."

Další věty

Vedle použití znamení prokazujícího rovnoběžnost letounů se v praxi můžete setkat s použitím dalších dvou vět. První je uvedena v následujícím tvaru: " Pokud je jedna ze dvou paralelních rovin rovnoběžná s třetí, druhá rovina je buď paralelní k třetí nebo rovnoběžně s ní ".

Na základě použití redukovatelných věty lze vždy dokázat rovnoběžnost rovin vzhledem k danému prostoru. Druhá věta ukazuje závislost rovin na kolmé přímce a vypadá takto: " Jsou-li dvě nekonkurenční roviny kolmé vzhledem k nějaké přímce, jsou považovány za rovnoběžné mezi sebou ".

Pojem nezbytných a dostatečných podmínek

Při řešení problémů prokázání rovnoběžnosti letounů několikrát byla odvozena nezbytná a dostatečná podmínka pro rovnoběžnost letounů. Je známo, že jakákoliv rovina je dána parametrickou rovnicí formy: A ₁ x + B ₁ y + C ₁ z + D ₁ = 0. Náš stav je založen na použití systému rovnic definujících uspořádání letounů ve vesmíru a je reprezentován následujícím textem: " Pro dokázání rovnoběžnosti dvou rovin je nezbytné a postačující, aby systém rovnic popisujících tyto roviny byl neslučitelný, tj. Nemá žádné řešení ."

Základní vlastnosti

Při řešení geometrických problémů však není použití funkce paralelního uspořádání dostatečné. Někdy vzniká situace, když je nutné prokázat paralelnost dvou či více linií v různých rovinách nebo rovnost segmentů uzavřených na těchto liniích. K tomu použijte vlastnosti paralelních rovin. V geometrii existují jen dva.

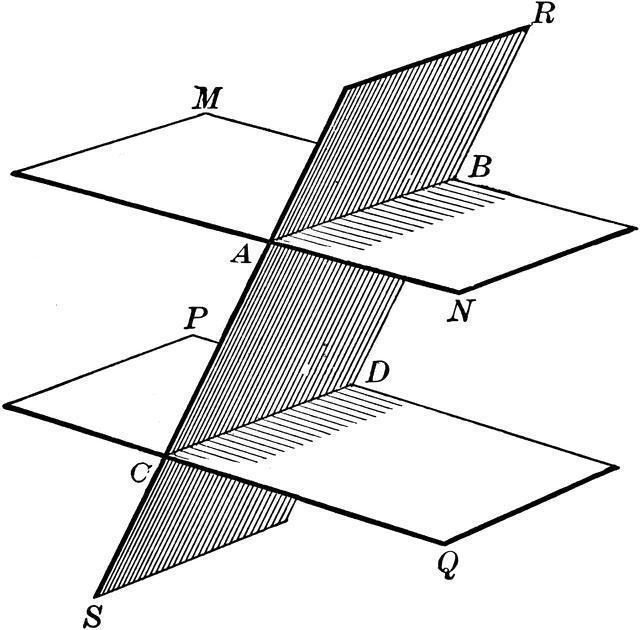
První vlastnost nám umožňuje posoudit rovnoběžnost linií v určitých rovinách a je zobrazena v následujícím tvaru: " Pokud se dvě paralelní roviny protínají třetí, pak čáry tvořené průsečíky budou také paralelní k sobě ."

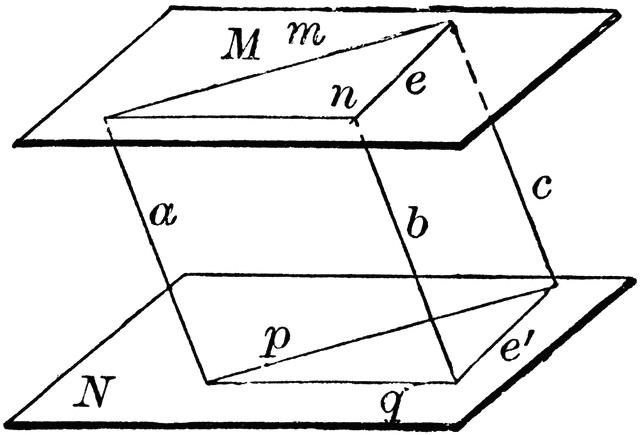
Významem druhé vlastnosti je prokázat rovnost segmentů umístěných na rovnoběžných přímkách. Jeho interpretace je uvedena níže. " Pokud budeme zvažovat dvě paralelní roviny a uzavřeme mezi nimi oblast, pak lze argumentovat, že délka segmentů tvořených touto oblastí bude stejná ."