Poincare hypotéza: historie problému, důkaz, význam

Ve škole jsou všichni obeznámeni s pojmy věta a hypotéza. Obvykle jsou v životě postiženy nejjednodušší a nejvíce primitivní zákony, zatímco matematici vytvářejí velmi složité předpoklady a představují zajímavé problémy. Ne vždy se jim podaří najít řešení a důkazy a v některých případech jejich následovníci a jen kolegové bojují po mnoho let.

Institut Clay v roce 2000 sestavil seznam 7 takzvaných tisíciletých výzvy obdobně jako seznam hypotéz sestavených v roce 1900. Téměř všechny tyto úkoly byly nyní vyřešeny, pouze jeden z nich přešel na aktualizovanou verzi. Seznam problémů je následující:

• Hodge hypotéza;
• rovnost tříd P a NP;
• Poincare hypotéza;
• Teorie Yang-Mills;
• Riemannova hypotéza;
• existence a hladkost řešení Navier-Stokesovy rovnice;
• Birch-Swinnerton-Dyerová domněnka.

Všichni patří do různých disciplín v rámci matematiky a jsou důležité. Například Navier-Stokesovy rovnice se vztahují k hydrodynamice, ale v praxi mohou popsat chování látky v pozemské magmatě nebo být užitečné při předpovědi počasí. Ale všechny tyto problémy stále hledají jejich důkaz nebo popření. Kromě jednoho.

Poincareova věta

Je poměrně obtížné jednoduše vysvětlit, jaký je problém, ale můžete to zkusit. Představte si kouli, například bublinu. Všechny body jeho povrchu jsou od středu rovnoběžné, což nepatří. Ale toto je dvourozměrné tělo a hypotéza hovoří o trojrozměrném těle. Je již nemožné si představit, ale máme teoretickou matematiku. V tomto případě bude samozřejmě také odstraněna všechna místa tohoto těla z centra.

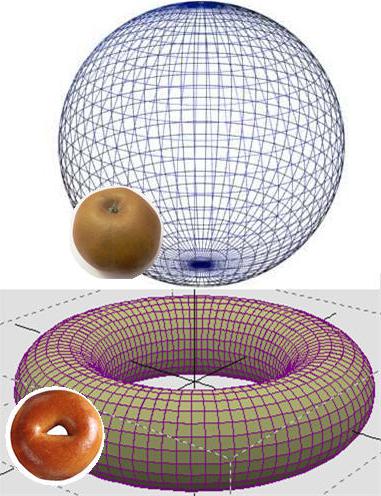
Tento problém se týká topologie - vědy o vlastnostech geometrických tvarů. A jedním ze základních pojmů v něm je homeomorfismus, tedy vysoký stupeň podobnosti. Chcete-li uvést příklad, můžete si představit kouli a torus. Jedna postava nemůže být získána od jiného, ​​aniž by došlo k rušení, ale kužel, kostka nebo válec z prvního lze snadno získat. Zde je hypotéza Poincare a je věnována těmto metamorfosům pouze s jedním rozdílem - mluvíme o vícerozměrném prostoru a tělech.

Dějiny

Francouzský matematik Henri Poincare studoval různé vědní obory. O jeho úspěších lze říci např. Skutečnost, že zcela nezávisle na Albert Einstein, předložil hlavní ustanovení speciální teorie relativity. V roce 1904 nastolil problém dokazování, že každé trojrozměrné tělo, které má určité vlastnosti koule, je přesně až na deformaci. Později byla rozšířena a zobecněna a stala se zvláštním případem Thurstonovy hypotézy formulované v roce 1982.

Znění

Poincaré zpočátku opustil takové prohlášení: každý jednoduše připojený kompaktní trojrozměrný rozdělovač bez hranic je homeomorfní k trojrozměrné sféře. Později byla rozšířena a zobecněna. A přesto po dlouhou dobu to byla hlavní úloha, která způsobila největší problémy a byla řešena až 100 let po jejím vzniku.

Výklad a smysl

To je homeomorfismus, o němž již bylo projednáno. Nyní stojí za to mluvit o kompaktnosti a jedinečnosti. První znamená jen to, že odrůda má omezené velikosti, nemůže být nepřetržitě a nekonečně roztažena.

Pokud jde o jedinečnost, můžete se pokusit uvést jednoduchý příklad. Dvourozměrná sféra - jablko - má jednu zajímavou vlastnost. Pokud používáte obvyklou uzavřenou gumu a připevníte ji k povrchu, může být hladká deformace snížena na jeden bod. To je vlastnost jedinečnosti, ale prezentovat ji ve vztahu k trojrozměrný prostor docela obtížné.

Jednoduše řečeno, problémem bylo prokázat, že singularita je jedinečná vlastnost pro danou oblast. A pokud relativně řečeno, zkušenost s gumovou kapelou skončila takovým výsledkem, pak je tělo homeomorfní. Pokud jde o aplikaci této teorie na život, Poincare věřil, že vesmír je v jistém smyslu trojrozměrnou sférou.

Důkaz o

Nemyslete si, že z těch desítek matematiků, kteří pracovali po celém světě, nikdo nedokázal pokročit v této otázce. Naopak, došlo k pokroku a nakonec vedlo k výsledku. Poincaré sám neměl čas dokončit práci, ale jeho výzkum seriózně rozšířil celou topologii.

Ve třicátých letech se zájem o hypotézu vrátil. Nejdříve bylo znění rozšířeno na "n-dimenzionální prostor" a poté americká Whitehead hlásila úspěšné důkazy a později ji opustila. V 60.-70s dva matematici najednou - Smale a Stallings - téměř současně, ale různými způsoby vyvinuli řešení pro všechny n větší než 4.

V roce 1982 a pro 4 byly nalezeny důkazy, zůstalo pouze 3, ve stejném roce Thurston formuloval hypotézu geometrizace a teorii Poincaré se staly jeho zvláštním případem.

Poté byla práce poněkud zablokována - americký Richard Hamilton navrhl používat řešení Ricci, ale dostal se do potíží a nedokončil výzkum.

Po dobu 20 let byla hypotéza Poincaré jako by zapomněla. V roce 2002 představil ruský matematik Grigori Perelman řešení obecně, o šest měsíců později, který doplnil. Později byly tyto důkazy testovány a přineseny "zářit" americkými a čínskými vědci. Zdálo se, že sám Perelman ztratil veškerý zájem o tento problém, i když vyřešil obecnější problém geometrizace, pro který je poincaré domněnka jenom zvláštním případem.

Uznávání a hodnocení

Samozřejmě, to se okamžitě stalo pocitem, protože řešení jednoho z problémů tisíciletí prostě nemohlo být přehlédnuto. Ještě překvapivější je skutečnost, že Gregory Perelman odmítl všechny ceny a ceny, říkat, že už měl nádherný život. V myslích obyčejných lidí se okamžitě stal příkladem toho napůl bláznivého génia, který se zajímá pouze o vědu.

To vše způsobilo v tisku a médiích spoustu diskuzí, že popularita matematika se stala jeho. V létě roku 2014 existovaly informace o tom, že Perelman šel do práce ve Švédsku, ale to se ukázalo být jenom pověstí, stále žije skromně v Petrohradě a stěží komunikuje s někým. Mezi cenami, které mu byly uděleny, nebyla jen cena Clay Institute, ale i prestižní Fieldsová medaile, ale vše odmítl. Nicméně, Hamilton, který podle Perelmanových odhadů neměl ani duležité příspěvky k důkazu, nebyl také zapomenut. V letech 2009 a 2011 získal i některé prestižní ceny a ceny.

Kulturní reflexe

Navzdory skutečnosti, že pro obyčejné občany není prohlášení a řešení tohoto problému málo smysluplné, důkazy se staly spíše známými. V roce 2008 natočil japonský režisér Masahito Kasuga dokument o dokumentu "Enchantment of Poincaré Hypothesis", který se věnuje 100 letým snahám o vyřešení tohoto problému.

Mnoho matematiků zapojených do tohoto problému se zúčastnilo střelby, ale hlavní postava, Grigory Perelmanová, to nechtěla dělat. Jeho více či méně blízkí přátelé se také podíleli na střelbě. Dokumentární film, který vyšel na obrazovkách v důsledku veřejného ohlasu o odmítnutí vědce přijmout cenu, získal slávu v určitých kruzích a také získal několik ocenění. Co se týče masová kultura, obyčejní lidé se stále ptají, jaké argumenty vedl Petersburgský matematik, odmítl vzít peníze, když mohl dát pryč, například na charitu.