Čtvercové rovnice. Řešení čtvercových rovnic
Zpočátku se toto téma může zdát komplikované kvůli mnoha ne příliš jednoduchým vzorcům. Nejen, že kvadratické rovnice samotné mají dlouhé vstupy, ale kořeny se také nacházejí prostřednictvím diskriminace. Existují celkem tři nové vzorce. Není moc snadné si vzpomenout. To je možné až po častém řešení těchto rovnic. Pak budou všechny vzorce vzpomínány samy.

Obecný pohled na kvadratickou rovnici
Zde je jim nabídnut výslovný záznam, když je nejprve zaznamenán nejvyšší stupeň, a pak - v sestupném pořadí. Často existují situace, kdy jsou komponenty v rozporu s ostatními. Pak je lepší přepsat rovnici v sestupném pořadí stupně proměnné.
Představujeme zápis. Jsou uvedeny v následující tabulce.
| Označení velikosti | Její jméno |
| a, b, c | koeficienty, které jsou libovolná čísla |
| x | proměnná |
| D | diskriminační |
| x 1 x 2 | kořeny rovnice |
Pokud přijmeme tyto notace, všechny kvadratické rovnice se zmenší na následující položku.
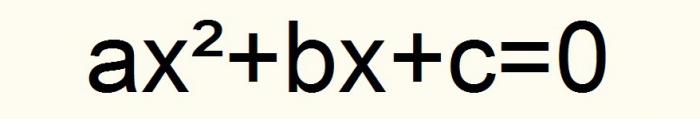
Navíc koeficient a ≠ 0. Nechte tento vzorec označit číslem jedna.
Když je daná rovnice, není jasné, kolik kořenů bude v odpovědi. Protože je vždy možná jedna ze tří možností:
- řešení bude mít dva kořeny;
- odpověď je jedno číslo;
- kořeny rovnice vůbec nebudou.
A zatímco rozhodnutí není dokončeno, je obtížné pochopit, které z možností se dostanou do konkrétního případu.
Typy záznamů čtvercových rovnic
V úlohách mohou být různé položky. Ne vždy budou vypadat jako obecný vzorec pro kvadratickou rovnici. Někdy bude chybět některé položky. To, co bylo napsáno výše, je úplná rovnice. Pokud v něm odstraníte druhý nebo třetí termín, získáte něco jiného. Tyto záznamy se také nazývají kvadratické rovnice, pouze neúplné.
Ad
Kromě toho mohou zmizet pouze termíny, jejichž koeficienty jsou "in" a "c". Číslo "a" nemůže být za žádných okolností nulové. Protože v tomto případě se vzorec změní na lineární rovnici. Vzorce pro neúplnou formu rovnic jsou následující:
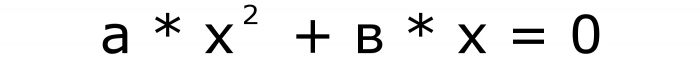
a
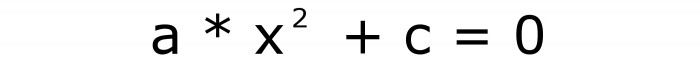
Takže existují pouze dva typy, kromě plných, jsou zde také neúplné kvadratické rovnice. Nechte první vzorec číslo dvě a druhé tři.
Diskriminační a závislost počtu kořenů na jeho hodnotě
Potřebujete znát toto číslo pro výpočet kořeny rovnice. Může se vždy vypočítat bez ohledu na vzorec kvadratické rovnice. Abyste mohli vypočítat diskriminaci, musíte použít níže uvedenou rovnici, která bude mít číslo čtyři.
Ad

Po nahrazení hodnot koeficientů v tomto vzorci můžete získat čísla s různými znaky. Pokud je odpověď ano, odpověď na rovnici bude mít dva různé kořeny. Se záporným číslem budou chybějící kořeny kvadratické rovnice. V případě rovnosti k nule bude odpověď jedna.
Jak je vyřešena kvadratická rovnice úplného formuláře?
Ve skutečnosti již tato otázka byla zvážena. Protože nejprve musíte najít diskriminaci. Jakmile je jasné, že existují kořeny kvadratické rovnice a jejich počet je znám, je nutné použít vzorce pro proměnné. Pokud existují dva kořeny, musíte použít tento vzorec.
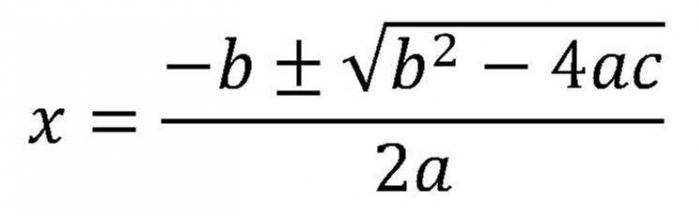
Protože je v něm znaménko "±", budou existovat dvě hodnoty. Druhý druhový výraz je diskriminační. Proto může být vzorec přepsán jiným způsobem.
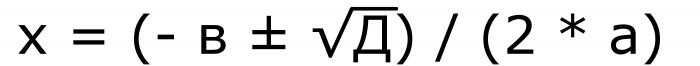
Formule 5. Ze stejného záznamu je zřejmé, že pokud je diskriminační nula, pak oba kořeny budou mít stejné hodnoty.
Pokud řešení kvadratických rovnic ještě nebylo vyřešeno, je lepší zapsat si hodnoty všech koeficientů před použitím diferenciálních a variabilních rovnic. Později tento okamžik nebude způsobovat potíže. Ale na samém začátku je zmatek.
Ad
Jak je řešena kvadratická neúplná rovnice?
Všechno je zde mnohem jednodušší. Dokonce ani není třeba dodatečné vzorce. A nepotřebují ty, které již byly zaznamenány pro diskriminující a neznámé.
Nejprve považujeme neúplnou rovnici číslo dvě. V této rovnováze se předpokládá, že se do závorky umístí neznámá hodnota a vyřeší se lineární rovnice, která zůstane v závorkách. Odpověď bude dva kořeny. První je nutně rovno nule, protože existuje faktor tvořený samotnou proměnnou. Druhý se ukáže při rozhodnutí lineární rovnice.
Neúplná rovnice číslo tři se řeší převodem čísla z levé strany rovnosti doprava. Potom musíte rozdělit koeficient směrem k neznámému. Zůstává pouze k získání druhá odmocnina a nezapomeňte jej zapsat dvakrát s opačnými znameními.

Užitečné tipy
Dále uvádíme několik akcí, které nám pomáhají naučit se řešit všechny druhy rovnosti, které se změní na kvadratické rovnice. Pomohou studentovi vyhnout se neopatrným chybám. Tyto nedostatky jsou příčinou špatných odhadů ve studiu rozsáhlého tématu "čtvercové rovnice (stupeň 8)." Následně nebudou tyto akce trvale provádět. Protože bude mít neustálé dovednosti.
Ad
- Nejprve musíte napsat rovnici ve standardním formuláři. To znamená, že nejprve termín s největším stupněm proměnné, a pak - bez stupně a poslední - jen číslo.
- Pokud se před součinitelem "a" objeví mínus, může to komplikovat práci začátečníku ke studiu kvadratických rovnic. Je lepší se ho zbavit. Za tímto účelem musí být rovnost vynásobena hodnotou "-1". To znamená, že všechny podmínky změní znak na opačné straně.
- Stejným způsobem se doporučuje zbavit se frakcí. Jednoduše vynásobte rovnici příslušným násobitelem, aby se jmenovatelé snížili.

Příklady
Vyžadují se následující kvadratické rovnice:
x 2 - 7x = 0;
5x 2 až 30 = 0;
15 - 2x - x 2 = 0;
x 2 + 8 + 3x = 0;
12x + x 2 + 36 = 0;
(x + 1) 2 x + 1 = (x + 1) (x + 2).
První rovnice: x 2 - 7x = 0. Je neúplná, proto je řešena tak, jak je popsáno pro vzorec dva.
Po vyjmutí závor, x (x - 7) = 0.
První kořen trvá na hodnotě: x 1 = 0. Druhá kořenová rovnice má x - 7 = 0. Je snadné si všimnout, že x 2 = 7.
Druhá rovnice: 5x 2 + 30 = 0. Opět neúplná. Řeší se pouze tak, jak je popsáno u třetího vzorce.
Po přenesení 30 na pravou stranu rovnice: 5x 2 = 30. Nyní musíte rozdělit na 5. Ukáže se: x 2 = 6. Odpovědi budou čísla: x 1 = √6, x 2 = - √6.
Třetí rovnice: 15 - 2x - x 2 = 0. Dále bude řešení kvadratických rovnic začínat jejich přepisováním do standardní formy: - x 2 - 2x + 15 = 0. Nyní je čas použít druhou užitečnou radu a vynásobit vše za mínus jeden . Ukazuje se x 2 + 2x - 15 = 0. Podle čtvrtého vzorce se musí vypočítat diskriminační faktor: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. Je to kladné číslo. Z toho, co bylo řečeno výše, se ukazuje, že rovnice má dva kořeny. Musí být vypočteny podle pátého vzorce. Znamená to, že x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Pak x 1 = 3, x 2 = - 5.
Ad
Čtvrtá rovnice x 2 + 8 + 3x = 0 převede na toto: x 2 + 3x + 8 = 0. Jeho diskriminant se rovná této hodnotě: -23. Vzhledem k tomu, že toto číslo je záporné, odpovědí na tento úkol bude následující položka: "Neexistují žádné kořeny".
Pátá rovnice 12x + x 2 + 36 = 0 by měla být přepsána následovně: x 2 + 12x + 36 = 0. Po uplatnění vzorce pro diskriminant získáme číslo nula. To znamená, že bude mít jeden kořen, a to: x = -12 / (2 * 1) = -6.
Šestá rovnice (x + 1) 2 + x + 1 = (x + 1) (x + 2) vyžaduje transformace, které spočívají v uvedení takových termínů na místo před otevřením konzol. Na místě prvního bude následující výraz: x 2 + 2x + 1. Po rovnosti se objeví tento záznam: x 2 + 3x + 2. Po počítání těchto pojmů bude rovnice vypadat takto: x 2 - x = 0. To se změnilo na neúplné . Stejně jako u něj byl již poněkud vyšší. Kořeny tohoto čísla budou čísla 0 a 1.