Pravoúhlý lichoběžník: všechny vzorce a příklady úkolů
Úkoly s lichoběžníkem se v řadě čísel, které byly dříve studovány, nezdají obtížné. Jako zvláštní případ je zvažován obdélníkový lichoběžník. A když hledáte její oblast, je někdy vhodnější ji rozdělit na dvě již známé: obdélník a trojúhelník. Jeden má jen trochu přemýšlet a existuje řešení.
Definice obdélníkového lichoběžníku a jeho vlastností
U libovolného lichoběžníku jsou základny rovnoběžné a strany mohou mít libovolnou hodnotu úhlů k nim. Pokud je zvažován obdélníkový lichoběžník, pak je v něm jedna ze stran vždy kolmá k základům. To znamená, že oba rohy v něm budou rovné 90 stupňům. Navíc vždy patří k sousedním vrcholům, nebo jinými slovy k jedné straně.
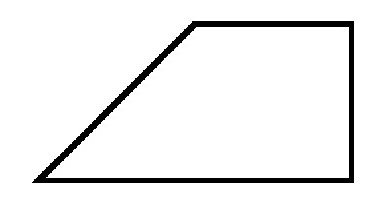
Jiné úhly v pravoúhlém lichoběžníku jsou vždy ostré a tupé. A jejich součet bude vždy roven 180 stupňům.
Každá diagonála se tvoří s menší stranou pravý trojúhelník. A výška, která je tažena z vrcholu tupým úhlem, rozděluje číslo na dvě. Jeden je obdélník a druhý pravý trojúhelník. Mimochodem, tato strana je vždy rovna výšce lichoběžníku.
Jaké názvy jsou přijaty ve vzorcích?
Všechny hodnoty použité v různých výrazech, které popisují lichoběžník, jsou okamžitě specifikovány a uvedeny v tabulce:
| Velikost | Jeho označení |
| a | větší základna |
| b | menší základna obdélníkového lichoběžníku |
| c, h | kolmo na základnu, výšku |
| d | šikmá strana |
| a | ostrý úhel |
| b | tupý úhel |
| m | lichoběžník střední čára |
| d 1 | menší úhlopříčka |
| d 2 | velká diagonála |
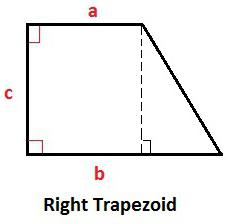
Vzorce, které popisují prvky obdélníkového lichoběžníku
Nejjednodušší z nich je výška a menší strana:
c = h.
Některé další vzorce pro tuto stranu obdélníkového lichoběžníku:
c = d * sina;
c = (a-b) * tg α;
c = √ (d 2 - (a - b) 2 ).
První z pravého trojúhelníku. A říká, že noha k hypotenze dává sinusu protilehlého úhlu.
Ve stejném trojúhelníku se druhá noha rovná rozdílu dvou základů. Proto je pravdivé tvrzení, které rovná dotyčnici úhlu k poměru noh.
Ze stejného trojúhelníku lze odvodit vzorec založený na znalosti Pythagorovy věty. Toto je třetí zaznamenaný výraz.
Mohou být napsány vzorce pro druhou stranu. Jsou také tři:
d = (a-b) / cosa;
d = c / sin a;
d = √ (c 2 + (a - b) 2 ).
První dva jsou opět získány z poměru stran ve stejném pravoúhlém trojúhelníku a druhý je odvozen z Pythagorovy věty.
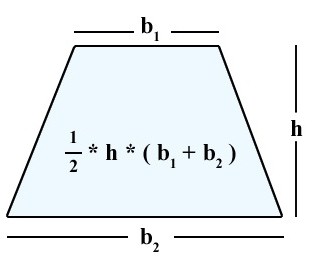
Jaký vzorec lze použít k výpočtu oblasti?
To, co je dáno pro libovolný lichoběžník. Pouze je nutné vzít v úvahu, že výška je stranou kolmá k základnám.
S = (a + b) * h / 2.
Tyto hodnoty nejsou vždy výslovně uvedeny. Proto pro výpočet plochy obdélníkového lichoběžníku je třeba provést některé matematické výpočty.
Co když potřebujete vypočítat úhlopříčku?
V tomto případě musíte vidět, že tvoří dva pravoúhlé trojúhelníky. Proto můžete vždy použít Pythagorovskou větu. Pak bude první úhlopříčka vyjádřena jako:
d1 = √ (c 2 + b 2 )
nebo jiným způsobem nahrazením "od" za "h":
d1 = √ (h 2 + b 2 ).
Podobně jsou získány vzorce pro druhou úhlopříčku:
d2 = √ (c 2 + b 2 ) nebo d 2 = √ (h 2 + a 2 ).
Číslo problému 1
Stav Plocha obdélníkového lichoběžníku je známá a je 120 dm 2 . Jeho výška je dlouhá 8 dm. Je nutné vypočítat všechny strany lichoběžníku. Další podmínkou je, že jedna základna je menší než druhá základna o 6 dm.
Rozhodnutí. Vzhledem k tomu, že je uveden obdélníkový lichoběžník, v němž je výška známa, můžeme okamžitě říci, že jedna strana se rovná 8 dm, tj. Menší straně.
Nyní můžete počítat další: d = √ (s 2 + (a - b) 2 ). A zde je okamžitě podána i strana s různými základnami. Druhý je 6 dm, to je známo ze stavu. Potom d bude rovno druhá odmocnina od (64 + 36), tedy od 100. Takže našla další stranu, která se rovná 10 dm.
Součet základů lze nalézt ze vzorce pro oblast. Bude se rovnat dvojnásobku hodnoty plochy vydělené výškou. Pokud se počítáte, ukáže to 240/8. Proto je součet základen 30 dm. Na druhou stranu jejich rozdíl je 6 dm. Kombinací těchto rovnic můžeme počítat obě základy:
a + b = 30 a a - b = 6.
Můžete vyjádřit jako (b + 6), nahradit ji v první rovnosti. Pak se ukáže, že 2b bude rovno 24. Proto jen b bude 12 dm.
Pak se poslední strana a rovná 18 dm.
Odpověď zní. Boky pravoúhlého lichoběžníku: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
Číslo problému 2
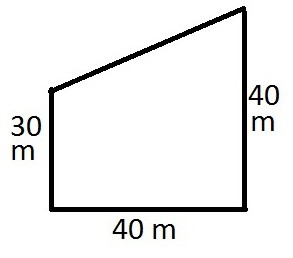
Stav S obdélníkovým lichoběžníkem. Jeho velká strana se rovná součtu základů. Jeho výška je 12 cm dlouhá. Je postavený obdélník, jehož strany se rovnají základně lichoběžníku. Je nutné vypočítat plochu tohoto obdélníku.
Rozhodnutí. Potřebujete začít s požadovaným. Požadovaná plocha je určena jako produkt a a b. Obě tato množství nejsou známa.
Bude vyžadováno použití dodatečných rovností. Jeden z nich je založen na prohlášení z podmínky: d = a + b. Pro tuto stranu je nutné použít třetí vzorec, který je uveden výše. Ukazuje se: d 2 = c 2 + (a - b) 2 nebo (a + b) 2 = c 2 + (a - b) 2 .
Je nutné provést transformaci, namísto její hodnoty nahradit podmínku - 12. Po otevření hranatých závorek a odlévání takových termínů se ukazuje, že 144 = 4 ab.
Na začátku rozhodnutí bylo řečeno, že a * b poskytuje požadovanou oblast. Proto v posledním výrazu můžete tento výrobek nahradit písmenem S. Jednoduchý výpočet poskytne hodnotu oblasti. S = 36 cm2.
Odpověď zní. Požadovaná plocha je 36 cm 2 .
Číslo problému 3
Stav Plocha obdélníkového lichoběžníku 150/3 cm2. Ostrý úhel je 60 stupňů. Úhel mezi malou a malou úhlopříčkou má stejnou hodnotu. Je třeba vypočítat menší diagonádu.
Rozhodnutí. Z vlastností lichoběžníkového úhlu se ukázalo, že jeho tupý úhel je 120 °. Pak ji diagonál rozdělí na rovnou, protože jedna část je již 60 stupňů. Úhel mezi touto diagonálou a druhou základnou je také 60 stupňů. To znamená, že trojúhelník tvořený velkou základnou, skloněnou stranou a menším úhlopříčkem je rovnostranný. Takže požadovaná diagonála se rovná a, stejně jako straně d = a.
Teď musíme zvážit správný trojúhelník. V tom je třetí úhel 30 stupňů. Takže noha ležící proti němu se rovná polovině hypotenze. To znamená, že menší základna lichoběžníku se rovná polovině požadované diagonály: b = a / 2. Z toho je nutné najít výšku rovnou straně, která je kolmá k základnám. Na straně je tady noha. Z Pythagorovy věty:
c = (a / 2) * √3.
Nyní zůstává pouze nahrazení všech hodnot do vzorce pro oblast:
150/3 = (a + a / 2) * (a / 2 * √3) / 2.
Řešení této rovnice dává kořen 20
Odpověď zní. Malá diagonála je dlouhá 20 cm.