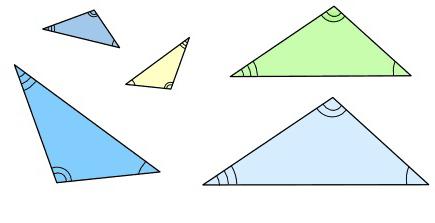
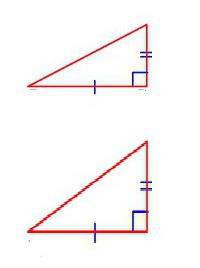
Známky podobnosti trojúhelníků a jejich praktické použití při řešení problémů

Pojem podobnosti je libovolný geometrické tvary v podstatě je velmi snadné vysvětlit a dokonce méně dokázat. Takže například při pohledu na objekt pomocí lupy vidíme obraz tohoto objektu několikrát rozšířen zachováním proporcí všech jeho velikostí. Jinými slovy, obraz objektu je podobný původnímu objektu před zvětšením. Ve většině problémů s geometrií, prokázat proporcionalitu stran a oblasti trojúhelníku použijte hlavní 3 znaky. Pro zvážení existujících známky podobnosti trojúhelníků je nutné nejprve definovat klíčový pojem, který bude v textu použit v budoucnu.

Takže trojúhelníky jsou podobné, pokud jsou jejich podobně umístěné strany úměrné a odpovídajícím způsobem uspořádané úhly jsou stejné (stojí za to pamatovat, že strany jsou nazývány podobnými, nebo odpovídají, pokud jsou umístěny proti stejným úhlům). Zvažte podobné trojúhelníky ΔABC a ΔA ₁ B ₁ C ₁ . Podle výše uvedeného konceptu jsou příslušnými stranami: AB a A ₁ B ₁ , jakož i páry stran BC a B ₁ C ₁ , AC a A ₁ C ₁ . Všimněte si, že strany každé z těchto tří dvojic leží protilehlých úhlů stejné velikosti.

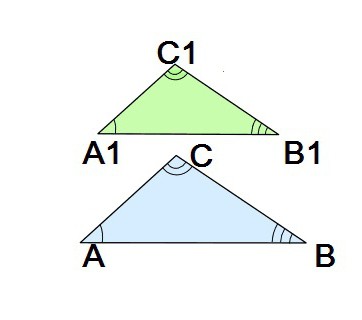Podobnost je označována jako zvláštní znak který je umístěn mezi označeními příslušných čísel: ΔABC ~ Δ A ₁ B ₁ C ₁ .

Poměr relevantních stran s přítomností této funkce je parametr nazvaný koeficient podobnosti k. Pokud k = 2, pak můžeme říci, že jedna ze dvou zvažovaných geometrických obrazců je zvětšená dvojitá kopie druhé. Je zřejmé, že pokud k = 1, potom jsou trojúhelníky stejné. Tuto rovnost lze považovat za zvláštní případ jejich podobnosti.

Známky podobnosti trojúhelníků

Ukazuje se, že pro zjištění přítomnosti uvažovaného prvku není nutné kontrolovat všechny požadavky uvedené ve výše uvedeném znění definice podobnosti. Stačí, abychom splnili minimální podmínky, a my to nyní potvrdíme v praxi.

První znamení

Při řešení problémů se první známka podobnosti trojúhelníků objevuje jako důkaz mnohem častěji než ostatní. Mějte na paměti, že funguje pouze s dvěma prvky geometrické postavy: dva úhly. Zbývající známky podobnosti trojúhelníků vyžadují účast tří prvků. Takže pro dva libovolné podobné trojúhelníky se 2 úhly jednoho z nich rovnají stejným 2 úhly druhého.

Důkaz o

Podle základních vlastností platných pro libovolný libovolný trojúhelník můžeme pro ∠C napsat následující výraz. Jeho hodnota bude stejná (180 ° - (∠А + ∠В)), pro další ∠С _{1 bude} hodnota vypočtena stejným principem. Základními transformacemi výrazů získáme, že ∠C = C ₁ . Takže všechny úhly přítomné v ΔАВС se rovnají všem analogickým úhlům umístěným v ΔA ₁ B ₁ С ₁ . Podobným algoritmem jsou prokázány zbývající známky podobnosti trojúhelníků.

Druhé znamení

Tento přístup k důkazu se často používá, pokud jsou známy úhly uvažovaných geometrických tvarů.

Pro dva podobné trojúhelníky je pravda, že obě strany každého z nich jsou úměrné k druhým podobným stranám druhého a úhly mezi těmito páry stran jsou stejné.

Důkaz o

Chcete-li tuto funkci prokázat, musíte se obrátit na předchozí výpočty. Na základě výše uvedených výsledků stačí prokázat, že ∠ Β = В ₁ . Zvažte ΔABC ₂ , pro které podle prvního znamení platí následující tvrzení: ∠1 = ∠А ₁ , ∠2 = В ₁ . ΔABC ₂ ~ ΔA ₁ В ₁ С ₁ . To znamená AB / A ₁ B ₁ = AC ₂ / A ₁ C. Na druhou stranu je známo z podmínky, že platí následující vztah: AC / A ₁ C _{1 =} AB / A ₁ B ₁ . V důsledku toho získáme rovnost stran AC = AC ₂ , stejně jako prohlášení, že ΔABC ~ ΔABC ₂ podle druhého znamení (AC = AC ₂ a ∠A = ∠1, jelikož v důsledku zvážení počátečních dat bylo zjištěno, že A = ∠A ₁ a ∠1 = ∠A ₁ , AB- je společná strana pro tyto dva trojúhelníky). Z důkazu vyplývá, že ∠B = ∠2, a protože ∠2 = ∠В ₁ , získáme ∠ Β = В ₁ . Z toho vyplývá, že je prokázáno další označení.

Třetí znamení

Tato vlastnost je považována za nejzřejmější při prokázání podobnosti, protože všechny strany těchto trojúhelníků se známými parametry jsou zvažovány.

Takže pro dva trojúhelníky, které se navzájem podobají, je uvedeno, že 3 strany jednoho z nich jsou úměrné 3 odpovídajícím stranám druhého.

Důkaz o

Vzhledem k předchozímu znaku podobnosti, nyní k vytvoření důkazu, stačí pouze zjistit, že existuje rovnost formu: ∠A = ∠A ₁ . Za tímto účelem zvážit libovolnou hodnotu ΔABC ₂ , pro kterou ∠1 = ∠A ₁ , 2 = В ₁ . Podle prvního atributu ΔABC ₂ ~ ΔA ₁ B ₁ C ₁ tedy pro tyto dva trojúhelníky můžeme napsat poměr typu AB / A ₁ B ₁ = BC ₂ / B ₁ C ₁ = C ₂ A / C ₁ A _1, ze kterého můžeme psát rovnost tvaru: B ₁ C ₁ = BC ₂ , A ₁ C ₁ = AC ₂ . Z toho je logické dospět k závěru, že ΔABC ~ ΔABC _2, a jako závěr, ∠A a ∠A ₁ jsou stejné. Z toho vyplývá, že uvažovaná funkce je rovněž prokázána.

Vlastnosti

1. U dvou trojúhelníků, které jsou vzájemně podobné, je poměr hodnot jejich ploch přímo úměrný koeficientu na čtvereč. Důkaz. Zvažte dvě libovolné postavy, které mají tři strany a tři úhly, které jsou navzájem podobné. Nechť A a A ₁ jsou odpovídající strany těchto obrazců a h a h ₁ jsou odpovídající výšce. Nechť k je koeficient podobnosti u zvažovaných trojúhelníků, proto z poměru stran můžeme napsat rovnici tvaru: A ₁ = k * A. Je snadné vidět, že pro výškový poměr můžeme napsat rovnici tvaru: h ₁ = k * h. Pro poměr ploch uvažovaných geometrických tvarů získáme: S ₁ / S = (1 / 2a ₁ h ₁ ) / (1 / 2ah) = (a ₁ / a) * (h ₁ / h) = k * k = k ² . Takže když je trojúhelník "roztažený" dvakrát, jeho plocha se zvyšuje o 2 ² = 4 krát. Druhá vlastnost vyplývá z předchozího důkazu a souvisí přímo s ním.
2. Všechny odpovídající čáry nakreslené v těchto trojúhelnících jsou také vzájemně úměrné a rovnají se hodnotě výše uvedeného koeficientu. To znamená, že podle výše uvedeného majetku lze tvrdit, že všechny vnitřní doplňkové konstrukce budou také úměrné.

Přidání k hlavnímu seznamu znaků

Za zmínku stojí řada jednotlivých prvků, které se vztahují na geometrické tvary určitého typu. Tak pravé trojúhelníky jsou podobné, pokud:

• jejich hypotenze a jakákoli ze dvou nohou jsou proporcionální;
• pokud jsou jejich odpovídající ostré úhly stejné;
• pokud jsou všechny nohy uvažovaných trojúhelníků párové proporcionální.

Závěr

Tak jsme spojili všechny možné znaky, pomocí kterých lze nějak dokázat podobnost dvou nebo více postav se třemi rohy a stranami, bez ohledu na jejich typ a vlastnosti. Ve většině problémů s geometrií se používají hlavní tři znaky k prokázání proporcionality stran a ploch, nicméně jsme nezohlednili řadu značek podobnosti, které jsou použitelné pouze tehdy, je-li nutné provést důkaz pro dotyčné geometrické postavy s pravým úhlem. Tyto známky podobnosti pravé trojúhelníky značně zjednoduší proces řešení různých druhů úkolů a vyžaduje pro ně minimální množství dat.