Jednoduché a ne tak způsoby, jak vypočítat kořenovou kostku

Kolik rozhořčených slov vyslovovalo v jeho adrese? Někdy se zdá, že kořenová krychle je neuvěřitelně odlišná od čtvercového. Ve skutečnosti rozdíl není tak velký. Zvláště pokud pochopíte, že jsou to jen konkrétní případy společného kořenu n-tého stupně.

Ale s jeho extrakce problémy mohou nastat. Ale nejčastěji jsou spojeny s těžkopádnými výpočty.

Co potřebujete vědět o kořenu libovolného stupně?

Za prvé, definice této koncepce. N-kořen nějakého "a" je takové číslo, které kdy exponentiace n dává originál "a".

A na kořeny jsou sudé a liché stupně. Je-li n rovno, může být radikál pouze nula nebo kladné číslo. V opačném případě nebude žádná skutečná odpověď.

Když je stupeň lichý, pak existuje řešení pro libovolnou hodnotu "a". Může to být také negativní.

Za druhé, kořenová funkce může být vždy zapsána jako stupeň, což je zlomek. Někdy je to velmi výhodné.

Například, "a" k síle 1 / n bude přesně kořen n-té síly "a". V tomto případě je základ stupně vždy větší než nula.

Podobně, "a" k moci n / m bude reprezentováno jako kořen mt síly z "a ⁿ ".

Za třetí, všechny akce se stupni jsou pro ně platné.

• Mohou být násobeny. Následně se exponenti přidávají.
• Kořeny lze rozdělit. Stupeň bude muset být odečten.
• A zvednout k síle. Pak by měly být násobeny. To je stupeň, který byl, na ten, na který budují.

Jaké jsou podobnosti a rozdíly mezi čtvercovými a krychlovými kořeny?

Jsou podobní, stejně jako bratři, pouze stupeň, který mají, je jiný. A princip výpočtu je stejný, jediný rozdíl je, kolikrát se číslo musí množit sám o sobě, aby získal radikální výraz.

A o významném rozdílu bylo řečeno trochu vyšší. Ale opakování nebude nadbytečné. Čtverec je extrahován pouze z ne záporného čísla. Zatímco je snadné vypočítat kořen kostky od záporné hodnoty.

Extrakce kubických kořenů na kalkulaci

Každý to někdy udělal druhá odmocnina. A co když je stupeň "3"?

Na běžnou kalkulačku je knoflík pouze pro čtverec, ale kubický není. To pomůže jednoduchému výčtu čísel, které se vynásobí třikrát. Získat radikální vyjádření? Tak to je odpověď. Nepracoval? Znovu zvedněte.

A co inženýrská forma kalkulačky v počítači? Hurá, existuje kubický kořen. Toto tlačítko lze jednoduše kliknout a program vám poskytne odpověď. Ale to není všechno. Zde můžete vypočítat kořen nejen 2 a 3 stupně, ale také libovolné. Protože existuje tlačítko, ve kterém je stupeň kořenu "y". To znamená, že po stisknutí tohoto tlačítka budete muset zadat další číslo, které se bude rovnat stupni kořenu a teprve potom "=".

Manuální extrakce kosti kořenů

Tato metoda je vyžadována, když kalkulačka není po ruce nebo ji nemůžete použít. Pak pro výpočet kořenové krychle čísla se vynaloží úsilí.

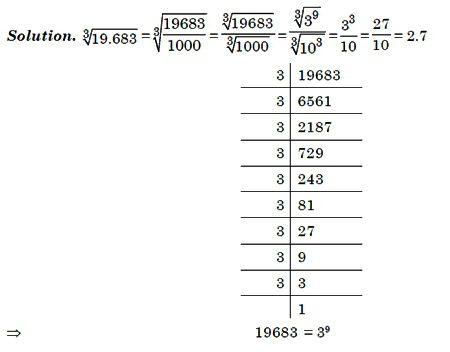
Nejprve zkontrolujte, zda není úplná krychle získána z libovolné celočíselné hodnoty. Možná je kořen 2, 3, 5 nebo 10 ve třetím stupni?

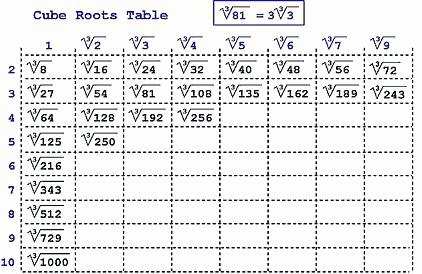
Jinak budete muset být považován za sloupec. Algoritmus není nejsnadnější. Ale pokud budete cvičit trochu, akce budou snadno pamatovat. A výpočet kořenové krychle už nebude problémem.

1. Mentálně rozdělte radikální výraz na tři číslice od desetinné čárky. Nejčastěji je potřeba částečná část. Pokud tomu tak není, nuly musí skončit.
2. Určete číslo, jehož kostka je menší než celá část radikálního výrazu. Napište jej do přechodové odpovědi nad kořenovým znaménkem. A pod touto skupinou umístit svou kostku.
3. Proveďte odečtení.
4. Přidejte první skupinu číslic do zbývající části.
5. V návrhu zadejte výraz: ² * 300 * x + a * 30 * x ² + x ³ . Zde "a" je střední odpověď, "x" je číslo, které je menší než výsledný zůstatek s přidělenými čísly.
6. Číslo "x" musí být napsáno za čárkou prozatímní odpovědi. A hodnota celého výrazu, který se má zapisovat pod srovnávanou bilanci.
7. Pokud je dostatečná přesnost, výpočty se zastaví. V opačném případě se musíte vrátit k položce číslo 3.

Ilustrativní příklad výpočtu kubického kořene

Je to potřeba, protože popis může vypadat komplikovaně. Následující obrázek ukazuje, jak extrahovat kořenovou kostku 15 na nejbližší stotinu.

Jedinou obtížností, kterou má tato metoda, je, že s každým krokem se čísla mnohonásobně zvětšují a stává se obtížnější počítat v liště.

1. 15> 2 ³ , pak pod celočíselnou částí 8 je napsáno a nad kořenem 2.
2. Po odečtení od 15 osmi získáme zbytek 7. Musíme přidat tři nuly.
3. a = 2. Proto: 2 ² * 300 * x + 2 * 30 * x ² + x ³ <7000 nebo 1200 x + 60 x ² x ³ <7000.
4. Metoda výběru ukazuje, že x = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Odčítání dává 1176 a číslo 4 se zobrazí nad kořenem.
6. Přiřadte ke zbytku tři nuly.
7. a = 24. Pak 172800 x + 720 x ² + x ³ <1176000.
8. x = 6. Výpočet výrazu udává výsledek 1062936. Zůstatek: 113064, nad kořenem 6.
9. Přiřaďte znovu nuly.
10. a = 246. Nerovnost se získá takto: 18154800x + 7380x ² + x ³ <113064000.
11. x = 6. Výpočty udávají číslo: 109194696, zůstatek: 3869304. Nad kořenem 6.

Odpověď je číslo: 2, 466. Vzhledem k tomu, že odpověď musí být věnována na stotiny, musí být zaokrouhlena: 2.47.

Neobvyklý způsob extrakce kubického kořene

Může se použít, pokud je odpověď celé číslo. Pak je kořen krychle extrahován rozložením radicand do lichých podmínek. Takové pojmy by navíc měly být minimálním možným počtem.

Například 8 je reprezentováno součtem 3 a 5. A 64 = 13 + 15 + 17 + 19.

Odpověď bude číslo, které se rovná počtu pojmů. Takže kubický kořen 8 se bude rovnat dvěma, a 64 - čtyři.

Pokud to stojí za kořen 1000, pak jeho rozklad na pojmy bude 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Celkem 10 pojmů. To je odpověď.