Některé informace o kostce a jak vypočítat plochu krychle

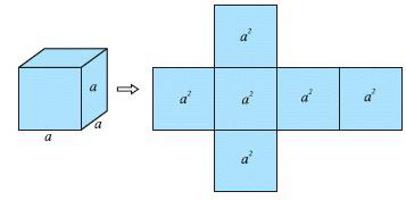
Kocka je úžasná postava. To je stejné na všech stranách. Každá jeho tvář se může okamžitě stát základnou nebo bokem. A to nic nezmění. A vzory pro to jsou vždy snadno zapamatovatelné. A bez ohledu na to, co potřebujete najít - objem nebo plochu krychle. V druhém případě se nemusí dokonce ani naučit něco nového. Stačí si pamatovat pouze čtvercový čtvercový vzorec.

Jaká je tato oblast?

Tato hodnota je obvykle označena latinským písmenem S. A to platí pro školní předměty, jako je fyzika a matematika. Měří se ve čtvercových jednotkách délky. Vše závisí na datech v problémech. Ty mohou být čtverečky mm, cm, m nebo km. A existují případy, kdy jednotky nejsou dokonce označeny. Jedná se jednoduše o číselný výraz oblasti bez názvu.

Takže jaká je tato oblast? Toto je množství, které je číselnou charakteristikou daného čísla nebo objemového tělesa. Zobrazuje velikost jeho povrchu, která je omezena stranami obrázku.

Jaký tvar se nazývá kostka?

Toto číslo je polyhedron. A není to snadné. Je pravdivý, to znamená, že má všechny prvky stejné. Ať už jsou to strany nebo hrany. Každý povrch krychle je čtvercový.

Jiný název pro kostku je pravidelný hexaedron, pokud je v ruštině, pak šestiúhelník. Může být tvořen čtyřhranným hranolem nebo rovnoběžkou. V závislosti na podmínkách, kdy jsou všechny hrany rovné a úhly tvoří 90 stupňů.

Tato postava je tak harmonická, že se často používá v každodenním životě. Například první hračky dítěte jsou kostky. A zábava pro ty, kteří jsou starší, je Rubikova kostka.

Jak je kostka spojena s jinými tvary a těly?

Pokud nakreslíte část krychle, která projde třemi tvářemi, bude mít druh trojúhelníku. Jak se vzdálenost od vrcholu zvyšuje, úsek se zvýší. Nastane chvíle, kdy se budou protínají 4 tváře a postava v sekci se stane čtyřúhelníkem. Pokud držíte část středu krychle tak, že je kolmá na její hlavní diagonály, dostanete se pravidelný šestiúhelník.

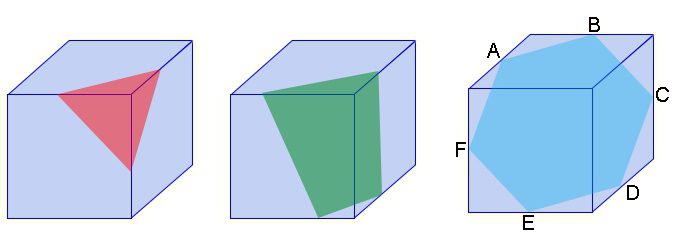
Uvnitř krychle můžete kreslit čtverec (trojúhelníkový pyramid). Pro horní část čtyřúhelníku se odebírá jeden z jeho rohů. Zbývající tři se shodují s vrcholy, které leží na opačných koncích okrajů vybraného úhlu krychle.

Můžete v něm zapsat osmikruh (konvexní pravidelný polyhedron, který vypadá jako dvě spojené pyramidy). Chcete-li to provést, najděte středy všech tváří krychle. Budou vrcholy oktahedronu.

Inverzní operace je také možná, to znamená, že uvnitř oktaedru je skutečně možné zadat kostku. Teprve nyní budou středy tváří prvního stane vrcholy pro druhé.

Metoda 1: Vypočtěte plochu krychle podle jejího okraje

Aby bylo možné vypočítat celou plochu krychle, vyžaduje se znalost jednoho z jejích prvků. Nejsnazší způsob, jak vyřešit, je situace, kdy je známá jeho hrana, nebo jinými slovy, strana náměstí, ze které se skládá. Tato hodnota je obvykle označena latinkou "a".

Teď musíme vzpomenout na vzorec, podle kterého je čtverec vypočítán. Aby se nezměnil, je jeho označení zavedeno písmenem S ₁ .

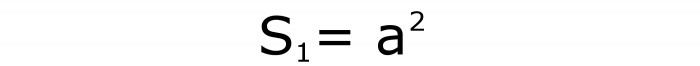
Pro větší pohodlí je lepší přiřadit čísla ke všem vzorcům. To bude první.

Ale je to jen jeden čtverec. Existuje šest z nich: 4 na bocích a 2 na dně a nahoře. Poté se plocha povrchu krychle vypočte podle následujícího vzorce: S = 6 * a ² . Její číslo je 2.

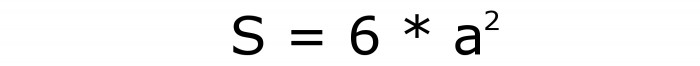
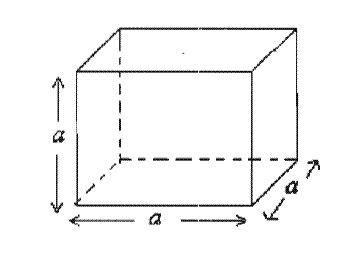
Metoda 2: Jak vypočítat plochu, pokud znáte objem těla

Tato metoda se snižuje tak, že počítá délku hrany známým objemem. A pak použijte známý vzorec, který je zde označen číslem 2.

Z matematického výrazu pro objem hexaedronu lze odvodit jeden, který může vypočítat délku hrany. Zde je:

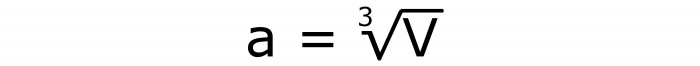
Číslování pokračuje a tady je číslo 3.

Nyní může být vypočítán a nahrazen do druhého vzorce. Pokud jednáme podle norem matematiky, pak musíme odvodit následující výraz:

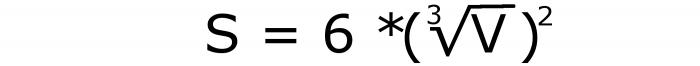
Toto je vzorec pro plochu celého povrchu krychle, který lze použít, pokud je znám objem. Toto číslo záznamu je 4.

Metoda 3: výpočet oblasti na úhlopříčce krychle

Chcete-li vypočítat plochu plného povrchu krychle, musíte také vykreslit hranu přes známou diagonádu. Používá vzorec pro hlavní diagonální hexaedron:

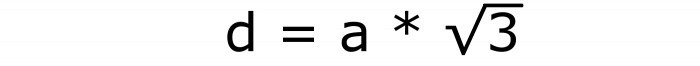
Jedná se o vzorec číslo 5.

Z toho je snadné odvodit výraz pro okraj krychle:

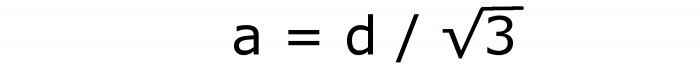
Toto je šestý vzorec. Po výpočtu můžete znovu použít vzorec pod druhým číslem. Ale je lepší psát toto:

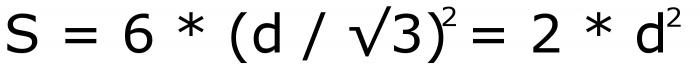
Ukazuje se, že je číslováno 7. Pokud se podíváte pozorněji, můžete vidět, že druhý vzorec je výhodnější než postupné výpočty.

Metoda 4: Použití poloměru zapsaného nebo ohraničeného kruhu pro výpočet plochy krychle

Pokud označíme poloměr kružnice popsané kolem hexahedronu písmenem R, pak se plocha povrchu krychle snadno vypočte podle následujícího vzorce:

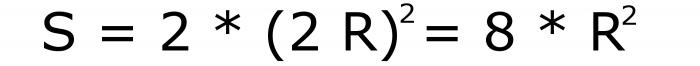
Sériové číslo je 8. Je snadno dosaženo vzhledem k tomu, že průměr kruhu se zcela shoduje s hlavní diagonále.

Označením poloměru zapsaného kruhu latinským písmenem r získáte následující vzorec pro plochu celého povrchu hexahedronu:

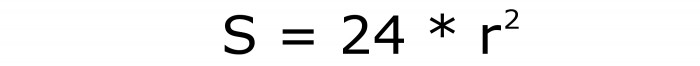
Toto je číslo vzorce 9.

Několik slov o bočním povrchu hexaedronu

Pokud problém vyžaduje nalezení oblasti bočního povrchu krychle, musíte použít již popsanou techniku. Když je okraj tělesa již daný, prostě čtverec čtverce musí být vynásoben číslem 4. Tato postava se objevila proto, že existují pouze 4 postranní plochy krychle. Matematická notace pro tento výraz je:

Její číslo je 10. Pokud jsou uvedeny jiné hodnoty, postupujte stejně jako metody popsané výše.

Příklady úkolů

Stav prvního. Známá plocha krychle. Je to 200 cm². Je třeba vypočítat hlavní úhlopříčku krychle.

Rozhodnutí.

1 způsob. Je třeba použít vzorec, který je označen číslem 2. Z něj bude jednoduché odvodit "a". Tento zápis matematiky bude vypadat druhá odmocnina z částečně se rovná S o 6. Po nahrazení čísel získáme:

a = √ (200/6) = √ (100/3) = 10 √3 (cm).

Pátý vzorec umožňuje okamžitou kalkulaci hlavní diagonály krychle. Chcete-li to provést, musíte vynásobit hodnotu okraje hodnotou √3. Je to jednoduché. Odpověď je, že úhlopříčka je 10 cm.

2 způsoby. V případě, že je vzorec pro úhlopříčku zapomenut, ale pamatuji si na Pythagorovu větu.

Stejně jako v první metodě najděte okraj. Poté musíte zapsat větu hypotenze dvakrát: první pro trojúhelník na obličeji, druhý pro ten, který obsahuje požadovanou diagonádu.

x2 = a² + a², kde x je úhlopříčka čtverce.

d² = x² + a² = a² + a² + a² = 3 a². Z tohoto záznamu je snadné vidět, jak se získá vzorec pro úhlopříčku. A pak budou všechny výpočty, stejně jako v první metodě. Je to trochu déle, ale dovolí vám, abyste si vzorec nepamatovali, ale sami si ho nechte zapamatovat.

Odpověď: diagonální krychle rovný 10 cm.

Druhá podmínka. Pro známou plochu, která se rovná 54 cm ² , vypočtejte objem krychle.

Rozhodnutí.

Pomocí vzorce pod druhým číslem musíte znát hodnotu okraje krychle. Jak je to provedeno, je podrobně popsáno v první metodě řešení předchozího problému. Po všech výpočtech dostaneme, že a = 3 cm.

Nyní musíte použít vzorec pro objem krychle, ve kterém je délka hrany zvýšena na třetí sílu. Proto bude objem považován za: V = 3 ³ = 27 cm ³ .

Odpověď: objem krychle je 27 cm3.

Stav třetího. Je nutné najít okraj krychle, pro kterou je splněna následující podmínka. Když se okraj zvýší o 9 jednotek, plocha celé plochy se zvýší o 594.

Rozhodnutí.

Vzhledem k tomu, že v problému neexistují žádné explicitní čísla, měl by být zaveden pouze další rozdíl mezi tím, co bylo a co se stalo. Je to snadné. Nechte požadovanou hodnotu rovnou "a". Pak zvětšený okraj krychle bude (a + 9).

Pokud to víte, musíte napsat vzorec pro plochu krychle dvakrát. První - pro počáteční hodnotu okraje - se shoduje s číslem 2. Číslo druhé se bude mírně lišit. V tom místo "a" musíte zapsat částku (a + 9). Vzhledem k tomu, že problém se zabývá rozdílem oblastí, musíme odečíst menší oblast z větší oblasti:

6 * (a + 9) ² až 6 * a ² = 594.

Transformace je nutné provést. Nejdříve vyhoďte 6 v levé části rovnosti a zjednodušte to, co zůstává v závorkách. Namístě (a + 9) ² - a ² . Zde je rozdíl čtverců, které lze převést následovně: (a + 9 - a) (a + 9 + a). Po zjednodušení výrazu získáme 9 (2a + 9).

Nyní se musí vynásobit číslem 6, tj. Číslem, které bylo před závorou ​​a rovno 594: 54 (2a + 9) = 594. Toto lineární rovnice s jedním neznámým. Jeho snadné řešení. Nejprve je třeba otevřít konzoly a potom přesunout dodatek s neznámou hodnotou na levou stranu rovnice a čísla na pravou stranu. Rovnice se ukáže: 2α = 2. Z toho je vidět, že požadovaná velikost se rovná 1.

Odpověď: a = 1.