Translační pohyb: definice, vzorce, věta

Mechanika zvažuje všechny možné pohyby materiálu a pevného těla. Všechny jsou popsány v několika částech. Například otázka, jak se pohybují, bude výsadou kinematiky. Podrobně popisuje translační pohyb, stejně jako komplexnější - rotační. Za prvé, to je jednodušší. Protože bez tohoto je obtížné přejít na následující témata.

Jaké předpoklady dovolí mechanik?

V mnoha problémech je dovoleno zavést aproximaci. To je způsobeno skutečností, že výsledky neovlivní, ale zjednoduší průběh uvažování.

První přiblížení se vztahuje k velikosti těla. Je-li zvažované tělo výrazně menší než jiné ve stejném referenčním rámci, pak jeho rozměry jsou zanedbávány. A samotné tělo se stává materiálním bodem.

Druhá je způsobena absencí deformace v těle během jeho pohybu. Nebo tak nevýznamná jeho velikost, která může být zcela zanedbána.

Jaký je translační pohyb těla?

Pro objasnění budete muset zvážit jakékoliv dva body uvnitř pevného tělesa. Musí spojit segment. Pokud je tento segment v průběhu pohybu paralelní s počáteční polohou, pak se říká, že jde o pohyb vpřed.

Pokud dojde k zanedbání velikosti těla a je zvažováno materiální bod Tento segment chybí a pohybuje se po samotné lince.

Živé příklady takového pohybu

První věc, kterou si pamatujete, je výtahové vozidlo. Dokonale ilustruje pohyb vpřed v těle. Výtah se vždy pohybuje přísně nahoru nebo dolů bez otáčení.

Následující příklad, který ilustruje translační pohyb, je pohyb kabiny ruského kola. To je však skutečné pouze v situaci, kdy se nepřihlíží k mírnému sklonu stánku na začátku každého offsetu.

Třetí situace, kdy je možné mluvit o pohybu vpřed, je spojena s pohybem pedálů jízdních kol. Jejich pohyb je považován za relativní k rámu. Zde se opět předpokládá, že nohy člověka se při jízdě nehoupají.

Seznam může být dokončen pohybem pístů, které kmitá ve válcích spalovacího motoru.

Hlavní pojmy

Kinematika translačního pohybu spočívá v tom, že studuje a popisuje pohyb těles a hmotných bodů. Neuvažuje však o důvodech, které toto tělo donutily. Chcete-li popsat pohyb, budou vyžadovány souřadnice pro označení jeho polohy v prostoru. Kromě toho je nutná znalost rychlosti a v daném okamžiku.

Za prvé, stojí za to pamatovat trajektorii. Je to čára, po níž se tělo pohybovalo.

První je zadání tahu. Je to vektor, který je označen latinským písmem r. Může spojit původ s polohou materiálu. V jiných případech je tento vektor odvozen od počátečního do koncového bodu trajektorie. Jednotky výtlaku jsou měřiče.

Druhou hodnotou, která si zaslouží pozornost, je cesta. To se rovná délce trajektorie, podél které se tělo pohybovalo. Cesta je označena písmenem latinská abeceda S, což je také měřeno v metrech.

Základní vzorce

Nyní je čas na rychlost. Ona je také vektor. Kromě toho charakterizuje nejen směr pohybu těla, ale i rychlost pohybu. Rychlostní vektor je vždy směrován podél dotyčnice, která může být přitahována k libovolnému bodu trajektorie. Označuje se písmenem V. Jednotky jeho měření jsou m / s.
Rychlost v každém okamžiku pohybu může být definována jako odvozenina pohybu v průběhu času. Pokud je problém v pořádku jednotný pohyb, pak platí následující vzorec:

• V = S: t, kde t je čas pohybu.

V situaci, kdy se změní směr pohybu, musíte použít součet všech pohybů.

Další hodnotou je zrychlení. Opět platí vektorové množství, které směřuje k rychlosti s velkou hodnotou. Je definována jako první derivace rychlosti v čase. Uznané označení - písmeno "a". Rozměr je uveden v m / s ² .

Vzorce pro každou složku zrychlení, směřující podél os, jsou vypočteny jako poměr změny rychlosti podél této osy k časovému intervalu. Pokud vytvoříte matematický záznam, získáte následující:

• a _x = ΔV _x : Δt.

Pro projekce zrychlení na jiné osy jsou vzorce podobné.
Kromě toho při zvažování pohybu po trajektorii s ohybem je možné vektor zrychlení rozložit na dva výrazy:

• a = a _t + a _n , kde _t je tangenciální zrychlení směřující podél ohybové tečny a _n je normální, což označuje střed zakřivení.

Translační pohyb jakéhokoli pevného těla je redukován na popis pohybu pouze jednoho z jeho bodů. Vzorce, které je třeba použít, jsou:

• S = S ₀ + V ₀ t + (při ² ): 2.
• V = V ₀ + na.

V tomto vzorci označují indexy "nula" počáteční hodnoty veličin.

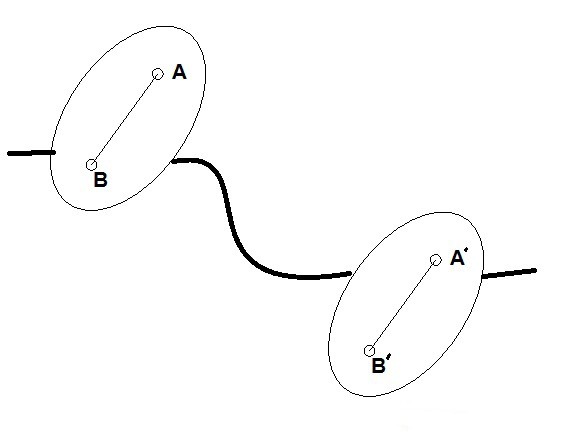
Věta o velikosti překladu

Jeho formulace je následující: trajektorie, rychlost a zrychlení všech bodů těla jsou stejné při jeho pohybu dopředu.

Abyste to dokázali, musíte napsat vzorec vektorové přírůstky posun a vektor spojující dva libovolné body. Trajektory všech bodů jsou získány díky jejich přenosu podél druhého vektoru. A to nezmění jeho směr a velikost v průběhu času. Proto lze argumentovat, že všechny body těla se pohybují po stejných trajektoriích.

Pokud budeme mít čas derivát, dostaneme hodnotu rychlosti. Navíc je výraz zjednodušený do té míry, že rychlost obou bodů je stejná.
Pole druhého časového odstupu je výsledkem rovnosti zrychlení obou bodů.