Trigonometrie od nuly: základní pojmy, historie

Sine, kosinus, tangent - když vyslovujete tato slova za přítomnosti studentů středních škol, můžete si být jisti, že dvě třetiny z nich ztratí zájem o další rozhovor. Důvod spočívá ve skutečnosti, že základy trigonometrie ve škole jsou učeny v úplné izolaci od reality, a proto studenti nevidí bod ve studiu formule a věty.

Ve skutečnosti, po bližším zkoumání, tato oblast znalostí se ukáže být docela zajímavá, stejně jako aplikovaná - trigonometrie nalezne uplatnění v astronomii, konstrukci, fyzice, hudbě a mnoha dalších oblastech.

Seznámíme se se základními pojmy a pojmenujeme několik důvodů pro studium této části matematiky.

Dějiny

Není známo, kdy lidstvo začalo vytvářet budoucí trigonometrii od začátku. Bylo však zdokumentováno, že již ve druhém tisíciletí před naším letopočtem Egypťané obeznámeni se základy této vědy: archeologové našli papyrus s úkolem, v němž je nutné nalézt úhel naklonění pyramidy na dvou známých stranách.

Závažnější úspěch dosáhli vědci starověkého Babylonu. Během staletí prováděli astronomii, zvládli řadu věty, zavedli zvláštní způsoby měření úhlů, které mimochodem využíváme dnes: stupně, minuty a sekundy vypůjčily evropská věda v řecko-římské kultuře, ve které tyto jednotky pocházely z Babylonců.

Předpokládá se, že slavná pythagorská věta týkající se základů trigonometrie byla babylonským známá téměř před čtyřmi tisíci lety.

Jméno

Doslova lze termín "trigonometrie" přeložit jako "měřící trojúhelníky". Hlavním předmětem studia v této části vědy po mnoho staletí byl pravý trojúhelník nebo spíše vztah mezi velikostí úhlů a délkami jeho stran (dnes začíná studie trigonometrie od začátku). V životě dochází k častým situacím, kdy nelze prakticky měřit všechny požadované parametry objektu (nebo vzdálenost k objektu), a pak je nutné získat chybějící údaje pomocí výpočtů.

Například v minulosti člověk nemohl měřit vzdálenost k prostorových objektů ale pokusy o výpočet těchto vzdáleností nastávají daleko před příchodem naší éry. Trigonometrie také hrála důležitou roli v navigaci: s určitými znalostmi, kapitán mohl vždy hýčkat v noci hvězdy a upravovat kurz.

Základní pojmy

Chcete-li zvládnout trigonometrii od začátku, musíte pochopit a zapamatovat si několik základních pojmů.

Síň určitého úhlu je poměr protilehlé nohy k hypotenze. Ujasňujeme si, že opačná noha je stranou proti úhlu, který uvažujeme. Takže pokud je úhel 30 stupňů, sinus tohoto úhlu bude vždy pro libovolnou velikost trojúhelníku ½. Kosinus úhlu je poměr sousední nohy k hypotenze.

Tangent je poměr protilehlé nohy k sousední (nebo rovnocenně poměr sinus k kosinus). Cotangent je jednotka dělená tečnou.

Za zmínku stojí známý Pi (3,14 ...), který představuje polovinu obvod s poloměrem jedné jednotky.

Oblíbené chyby

Lidé, kteří studují trigonometrii od začátku, dělají řadu chyb - většinou z nedbalosti.

Za prvé, při řešení problémů v geometrii je třeba si uvědomit, že použití sinusů a kosinů je možné pouze v pravoúhlém trojúhelníku. Stává se, že student "na stroji" zaujme nejdelší stranu trojúhelníku pro hypotenzu a dostane nesprávné výsledky výpočtů.

Za druhé, nejprve je snadné zaměnit hodnoty sinusu a kosinusu pro zvolený úhel: připomínáme, že sinus 30 stupňů je číselně shodný s kosinem 60 a naopak. Při nahrazení nesprávného čísla budou všechna další výpočty chybná.

Zatřetí, dokud není problém zcela vyřešen, neměli byste zaokrouhlit žádné hodnoty, extrahovat kořeny, zapsat obyčejnou zlomek jako desetinnou hodnotu. Často studenti usilují o získání "krásného" čísla v problémech trigonometrie a okamžitě extrahují kořen od tří, i když v přesně jedné akci může být tento kořen snížen.

Etymologie slova "sinus"

Historie slova "sinus" je opravdu neobvyklá. Faktem je, že doslovný překlad tohoto slova z latiny znamená "dutý". Je to proto, že při překládání z jednoho jazyka do druhého došlo ke ztrátě správného chápání slova.

Názvy základních trigonometrických funkcí pocházejí z Indie, kde koncept sinusu byl označen slovem "bowstring" v Sanskritě - skutečností je, že segment spolu s obloukem kruhu, na kterém byl založen, připomínal luk. Během rozkvětů arabské civilizace byly zapůjčeny indické úspěchy v oblasti trigonometrie a termín byl převeden na arabštinu ve formě přepisu. Stalo se tak, že v tomto jazyce už bylo podobné slovo, které označuje dutinu, a pokud Arabové pochopili fonetický rozdíl mezi rodilým a vypůjčeným slovem, pak Evropané, kteří překládali vědecké ústavy do latiny doslovně překládali arabské slovo, žádný vztah k pojmu sinus . Používáme je dodnes.

Tabulky hodnot

Existují tabulky, ve kterých jsou zadávány číselné hodnoty pro sinusy, kosinusy a dotyky všech možných úhlů. Níže uvádíme údaje pro úhly 0, 30, 45, 60 a 90 stupňů, které je nutno naučit jako povinnou sekci trigonometrie pro figuríny. Výhoda zapamatování je poměrně snadná.

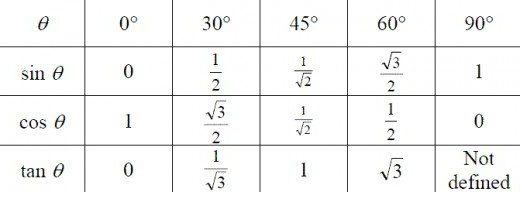Pokud se stane, že číselná hodnota sinus nebo kosinus úhlu "vyletěl z hlavy", existuje způsob, jak to odvodit sami.

Geometrické znázornění

Nakreslíme kružnici a do jejího středu nakreslíme osy a osy. Osa úsečky je umístěna horizontálně, osa osy je svislá. Obvykle jsou označeny jako "X" a "Y". Teď ze středu kruhu nakreslíme čáru tak, aby byl získán požadovaný úhel mezi osou X a osou X. Konečně z bodu, kde přímka protíná kružnici, snížíme kolmici na osu X. Délka výsledného segmentu bude rovna číselné hodnotě sinusu našeho úhlu.

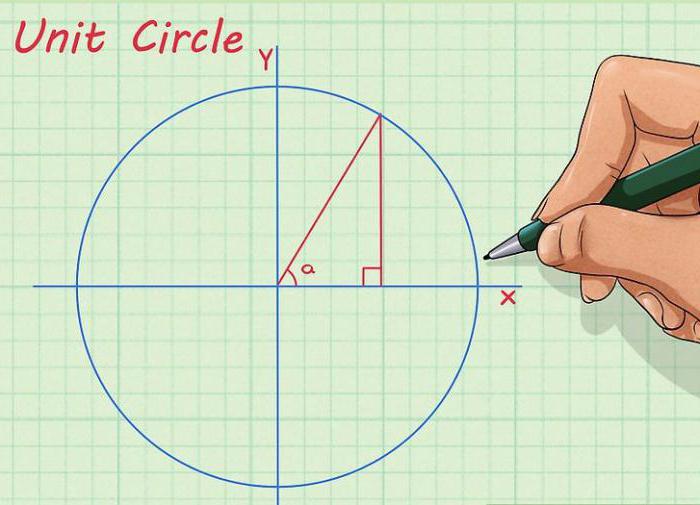Tato metoda je velmi relevantní, pokud jste zapomněli požadovanou hodnotu, například na zkoušce, a neexistuje učebnice o trigonometrii po ruce. Tímto způsobem nebudete mít přesné číslo, ale určitě uvidíte rozdíl mezi ½ a 1,73 / 2 (sinus a kosinus o úhlu 30 stupňů).

Aplikace

Jedním z prvních specialistů, kteří používali trigonometrii, byli námořníci, kteří na otevřeném moři neměli žádný jiný referenční bod, kromě oblohy nad jejich hlavami. Dnes kapitáni lodí (letadla a jiné druhy dopravy) Nehledají nejkratší cestu hvězdami, ale aktivně využívají GPS navigaci, což by bylo bez použití trigonometrie nemožné.

Takřka v každém fyziky Čekáte na výpočty pomocí sines a cosinů: zda se jedná o aplikaci síly v mechaniky, výpočty dráhy objektů v kinematikách, oscilace, šíření vln, refrakce světla - prostě nemůžete bez základní trigonometrie ve vzorcích.

Další profesí, která je bez trigonometrie nemyslitelná, je geodet. Pomocí teodolitu a úrovně nebo složitějšího zařízení - tachymetru, tito lidé měří rozdíl v výšce mezi různými body na povrchu země.

Opakovatelnost

Trigonometrie se zabývá nejen úhly a stranami trojúhelníku, i když od tohoto okamžiku začala svou existenci. Ve všech oblastech, kde existuje cyklicita (biologie, lékařství, fyzika, hudba atd.), Se setkáte s plánem, jehož jméno pravděpodobně znáte, je sinusová vlna.

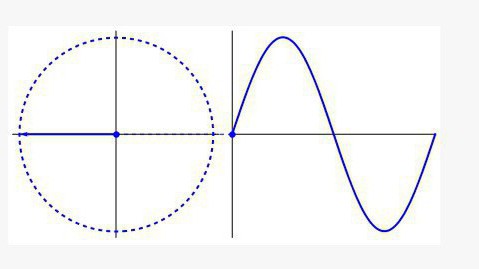Takový graf je kružnice vyvinutá podél časové osy a vypadá jako vlna. Pokud jste někdy pracovali s osciloskopem ve třídě ve fyzice, pochopíte, o čem to jde. Jak hudební ekvalizér, tak zařízení zobrazující srdeční rytmy používají ve své práci trigonometrické vzorce.

Na závěr

Přemýšlející o tom, jak se učit trigonometrii, většina středních a středních škol začne považovat za složitou a nepraktickou vědu, protože se seznámí jen s nudnými informacemi z učebnice.

Vzhledem k nepraktičnosti jsme již viděli, že v různých mírách je potřeba pracovat s sinusy a dotyky v téměř každé oblasti činnosti. Pokud jde o složitost ... Myslím, že pokud by lidé používali toto znalosti před více než dvěma tisíci lety, kdy dospělý měl méně znalostí než dnešní student střední školy, je skutečně možné, abyste studoval tuto vědní oblast na základní úrovni? Několik hodin promyšlených lekcí s řešením problému - a svůj cíl dosáhnete studiem základního kurzu, takzvané trigonometrie pro figuríny.