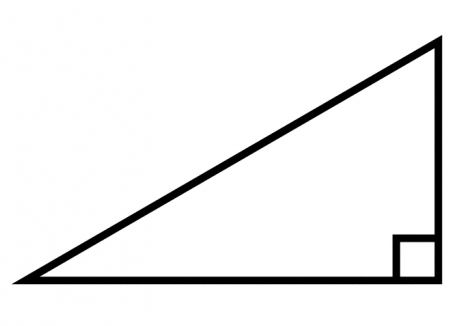
Druhy trojúhelníků. Úhly trojúhelníku

Nejjednodušší polygon, který je studován ve škole, je trojúhelník. Je pro studenty srozumitelnější a setkává se s menšími potížemi. Přes skutečnost, že existují různé typy trojúhelníků, které mají zvláštní vlastnosti.

Jaký tvar se nazývá trojúhelník?

Tvořena třemi body a segmenty. První se nazývají vrcholy, druhé strany. Navíc všechny tři segmenty by měly být spojeny tak, aby mezi nimi vytvářely úhly. Jméno figurky "trojúhelník".

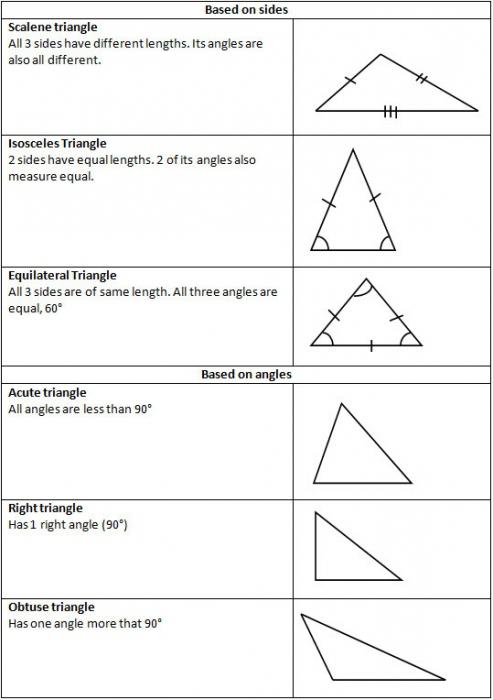
Rozdíly v názvech rohů

Vzhledem k tomu, že mohou být ostré, tupé a rovné, potom jsou tyto typy trojúhelníků určovány těmito názvy. Existují tedy tři skupiny těchto čísel.

• První. Pokud jsou všechny rohy trojúhelníku akutní, bude mít název ostrého úhlu. Všechno je logické.

• Druhý. Jeden z rohů je tupý, což znamená trojúhelníkový roh. Prostě není místo.

• Třetí. Existuje úhel 90 stupňů, který se nazývá rovný. Trojúhelník se stává pravoúhlým.

Rozdíly v názvech po stranách

V závislosti na vlastnostech stran jsou tyto typy trojúhelníků odlišné:

• obecný případ je všestranný, ve kterém všechny strany mají libovolnou délku;

• isosceles, jejichž obě strany mají stejné číselné hodnoty;

• rovnostranné, délky všech stran jsou stejné.

Pokud úloha nezadá specifický typ trojúhelníku, musíte nakreslit libovolný. Ve kterém jsou všechny úhly ostré a strany mají různé délky.

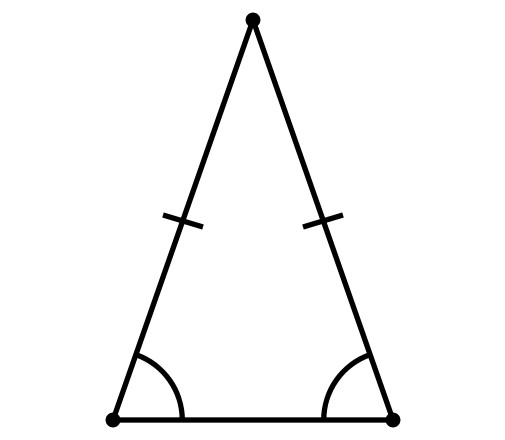
Vlastnosti společné všem trojúhelníkům

1. Pokud přidáte všechny rohy trojúhelníku, získáte číslo rovné 180 °. A bez ohledu na to, jak vypadá. Toto pravidlo je vždy platné.
2. Číselná hodnota každé strany trojúhelníku je menší než ostatní dvě dohromady. Současně je to víc než jejich rozdíl.
3. Každý vnější roh má hodnotu, která se získá přidáním dvou vnitřních, nikoliv sousedních. Navíc je vždy více než vnitřní, přilehlé k němu.
4. Naproti malé straně trojúhelníku je vždy nejmenší úhel. Naopak, pokud je strana velká, pak bude úhel největší.

Tyto vlastnosti jsou vždy platné bez ohledu na to, jaký druh trojúhelníků jsou v problémech brány v úvahu. Všechny ostatní vycházejí ze specifických rysů.

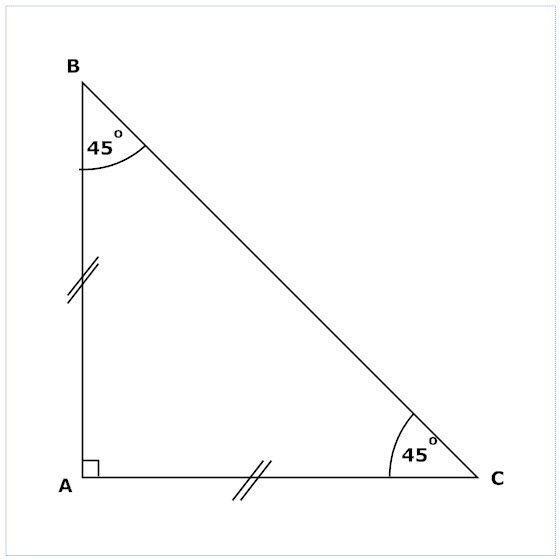
Vlastnosti rovnoramenného trojúhelníku

• Úhly, které sousedí se základnou, jsou stejné.
• Výška, která je držena na základně, je také střední a průsečík.
• Výšky, mediány a bisektory, které jsou postaveny na stranách trojúhelníku, jsou vzájemně stejné.

Vlastnosti rovnostranného trojúhelníku

Pokud je taková postava, pak všechny výše popsané vlastnosti budou pravdivé. Protože rovnostrannost bude vždy rovnoměrná. Ale ne naopak, rovnoramenný trojúhelník nemusí být nutně rovnostranný.

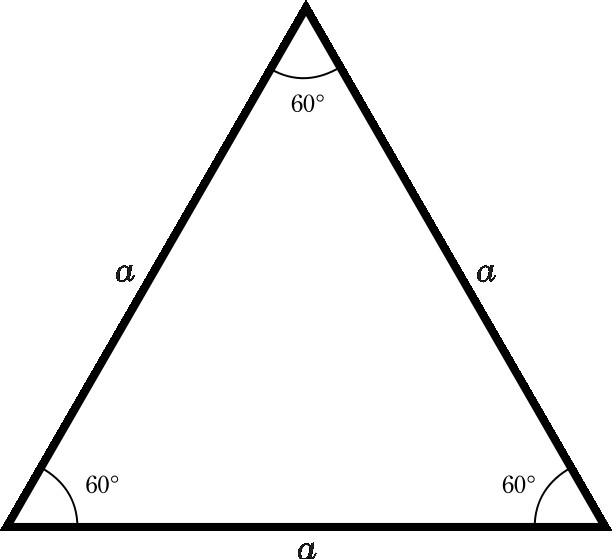
• Všechny úhly jsou stejné a mají hodnotu 60 °.
• Jakákoli střední hodnota rovnostranného trojúhelníku je její výška a průsečík. A jsou všichni rovní. K určení jejich hodnot existuje vzorec, který se skládá z produktu strany druhá odmocnina z 3 dělených 2.

Vlastnosti pravého trojúhelníku

• Dva akustické úhly udávají celkovou hodnotu 90 °.
• Délka hypotenze je vždy větší než délka nohou.
• Číselná hodnota mediánu provedeného na hypotenze je polovina.
• Stejná hodnota se rovná noze, pokud leží proti úhlu 30 °.
• Výška, která je vyvedena z vrcholu o hodnotu 90 °, má určitou matematickou závislost na nohách: 1 / n ² = 1 / a ² + 1 / v ² . Zde: a, c - nohy, n - výška.

Úkoly s různými typy trojúhelníků

№1. Je dán rovnoramenný trojúhelník. Její obvod je známý a je 90 cm. Je nutné znát jeho strany. Jako dodatečná podmínka: strana je menší než základna o 1,2 krát.

Řešení

Hodnota obvodu je přímo závislá na hodnotách, které je třeba nalézt. Součet všech tří stran dá 90 cm. Teď musíme vzpomenout na znamení trojúhelníku, ve kterém je to rovnoramenné. To znamená, že obě strany jsou stejné. Můžete vytvořit rovnici se dvěma neznámymi: 2a + b = 90. Zde je a strana, v - základně.

Jedná se o další podmínku. Následuje druhá rovnice: v = 1,2a. Tento výraz můžete nahradit v prvním. Ukazuje se: 2a + 1,2a = 90. Po přeměnách: 3.2a = 90. Odtud a = 28.125 (cm). Nyní je snadné zjistit základ. To se nejlépe provádí z druhé podmínky: c = 1,2 * 28,125 = 33,75 (cm).

Pro kontrolu můžete přidat tři hodnoty: 28.125 * 2 + 33.75 = 90 (cm). To je správné.

Odpověď: strany trojúhelníku jsou 28.125 cm, 28.125 cm, 33.75 cm.

№2. Strana rovnostranného trojúhelníku je 12 cm. Je nutné vypočítat jeho výšku.

Rozhodnutí. Chcete-li vyhledat odpověď, stačí se vrátit do bodu, kde byly popsány vlastnosti trojúhelníku. Toto je vzorec pro nalezení výšky, mediánu a bisektoru rovnostranného trojúhelníku.

n = a * √3 / 2, kde n je výška a a je strana.

Náhrada a výpočet poskytují následující výsledek: n = 6 √3 (cm).

Tento vzorec si nemusí pamatovat. Postačuje připomenout, že výška rozděluje trojúhelník na dva obdélníkové. Navíc se ukazuje, že jde o nohu a hypotenze v ní je strana původního, druhá noha je polovina známé strany. Nyní musíte napsat Pythagorean větu a odvodit vzorec pro výšku.

Odpověď: výška je 6 √ 3 cm.

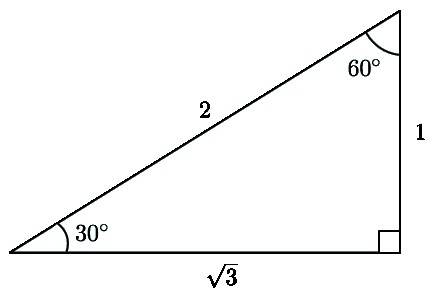
№3. Dává se mu MKR - trojúhelník, ve kterém je úhel K. Kryty MR a KR jsou známy, jsou stejné jako 30 a 15 cm. Je nutné zjistit hodnotu úhlu R.

Rozhodnutí. Pokud uděláte výkres, je zřejmé, že MR je hypotenze. A to je dvakrát noha KR. Opět musíte se obrátit na vlastnosti. Jeden z nich je spojen s rohy. Z toho je zřejmé, že úhel CMR se rovná 30 °. Takže požadovaný úhel P bude rovný 60 °. To vyplývá z jiné vlastnosti, která uvádí, že součet dvou ostrých úhlů by měl být 90 °.

Odpověď: Úhel P je 60 °.

№4. Musíte najít všechny úhly rovnoramenného trojúhelníku. O něm je známo, že vnější úhel od úhlu u základny je 110 °.

Rozhodnutí. Vzhledem k tomu, že je uveden pouze vnější kout, je třeba jej použít. Formuje se s vnitřním úhel rozvinutý. Celkově tedy dávají 180 °. To znamená, že úhel na základně trojúhelníku bude roven 70 °. Vzhledem k tomu, že jde o rovnoběžnost, má druhý úhel stejný význam. Zbývá vypočítat třetí úhel. Ve vlastnostech společných pro všechny trojúhelníky je součet úhlů 180 °. Třetí je tedy definována jako 180 ° - 70 ° - 70 ° = 40 °.

Odpověď: úhly jsou 70 °, 70 °, 40 °.

5. Je známo, že v rovnoměrném trojúhelníku je úhel ležící oproti základně 90 °. Na základě vyznačeného bodu. Segment, který jej spojuje s pravým úhlem, ji dělí v poměru 1 k 4. Musíte znát všechny úhly menšího trojúhelníku.

Rozhodnutí. Jeden z rohů lze okamžitě identifikovat. Od pravý trojúhelník a rovnoběžky, pak ty, které leží na jeho základně, budou 45 °, tj. 90 ° / 2.

Druhá z nich pomůže nalézt známý vztah stavu. Vzhledem k tomu, že se rovná 1 až 4, pak části, do kterých je rozdělena, jsou získány pouze 5. Pro zjištění menšího úhlu trojúhelníku tedy potřebujete 90 ° / 5 = 18 °. Zbývá se naučit třetí. Chcete-li to provést, odečtěte od 180 ° (součet všech úhlů trojúhelníku) 45 ° a 18 °. Výpočty jsou jednoduché a vyrazí: 117º.

Odpověď: 18º, 45º, 117º