Co je to pravé šestiúhelník a jaké úkoly s ním mohou být spojeny?

Nejznámější postava, která má více než čtyři rohy - je pravidelný šestiúhelník. V geometrii se často používá v problémech. A v životě je přesně tento typ plástového plátna na řezu.

Jak se liší od špatného?

Nejprve je šestiúhelník číslice se 6 vrcholy. Za druhé, může být konvexní nebo konkávní. První se vyznačuje skutečností, že čtyři vrcholy ležely na jedné straně přímé čáry, která procházela dvěma dalšími.

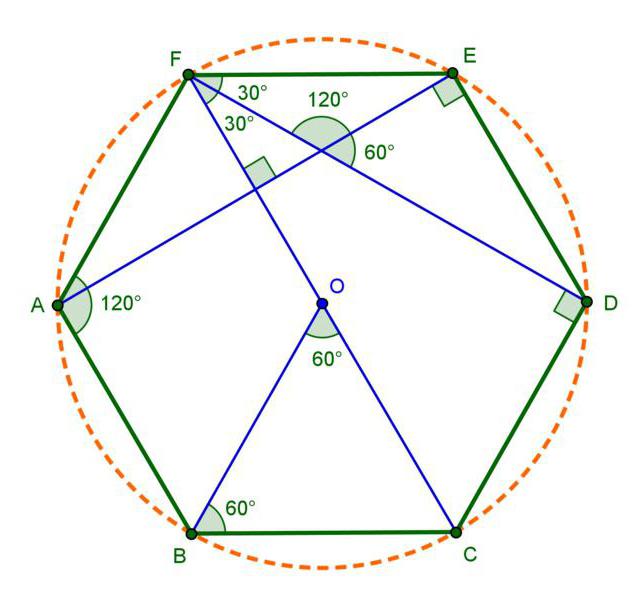
Za třetí, pravidelný šestiúhelník je charakterizován skutečností, že všechny jeho strany jsou stejné. Každý roh čísla má navíc stejnou hodnotu. Chcete-li určit součet všech úhlů, musíte použít vzorec: 180 ° * (n - 2). Zde n je počet vrcholů tvaru, tj. 6. Jednoduchý výpočet udává hodnotu 720 °. To znamená, že každý úhel je 120 stupňů.

V každodenních činnostech se pravidelný šestiúhelník nachází ve sněhové vločce a ořechu. Lékárníci to vidí i v benzenové molekule.

Jaké vlastnosti je třeba znát při řešení problémů?

K výše uvedenému přidejte:

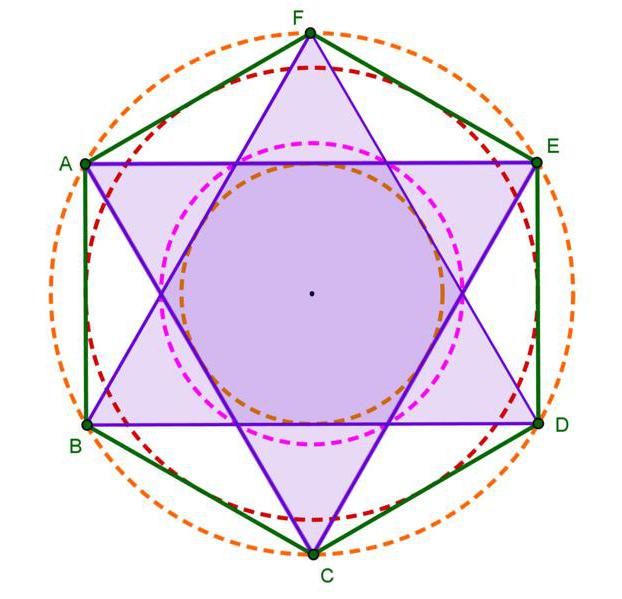
• diagonální postavy, které procházejí středem, rozdělí to na šest trojúhelníků, které jsou rovnostranné;
• strana pravidelného šestiúhelníku má hodnotu, která se shoduje s poloměrem kružnice popsané kolem.
• pomocí takového tvaru je možné naplnit rovinu a mezi nimi nebude žádná mezera a žádné překryvy nebudou.

Představení označení

Tradičně na pravé straně geometrický tvar označené latinkou "a". Chcete-li vyřešit problémy, potřebujete další oblast a obvod, jsou to S a P. Kruh je napsán v pravidelném šestiúhelníku nebo je popsán kolem něj. Potom se zadávají hodnoty pro jejich poloměry. Označují se písmeny r a R.

V některých vzorcích se objevují vnitřní úhel, poloměr a apothem (který je kolmý ke středu obou stran od středu polygonu). Pro ně jsou písmena použita: α, p, m.

Vzory, které popisují tvar

Pro výpočet poloměru zapsaného kruhu potřebujete následující: r = (a * √3) / 2, kde r = m. To znamená, že stejný vzorec bude pro apothemy.

Vzhledem k tomu, že obvod šestiúhelníku je součtem všech stran, je definován jako: P = 6 * a. Vzhledem k tomu, že strana je rovna poloměru obvodového obvodu, pro obvod je takový vzorec pro pravidelný šestiúhelník: P = 6 * R. Od daného pro poloměr zapsaného kruhu je odvozen vztah mezi a a r. Pak vzorec má následující formu: P = 4 r * √3.

Pro oblast pravidelného šestiúhelníku to může být užitečné: S = p * r = (a ² * 3 √3) / 2.

Úkoly

Č. 1. Podmínka. Tam je pravidelný hexagonální hranol, každý okraj je 4 cm. Obsahuje válec, jehož objem je třeba vědět.

Rozhodnutí. Hlučnost válce je definován jako produkt základní plochy a výšky. Druhý se shoduje s hranou hranolu. A to se rovná straně pravidelného šestiúhelníku. To znamená, že výška válce je také 4 cm.

Chcete-li zjistit plochu základny, musíte vypočítat poloměr kružnice v šestiúhelníku. Vzorec pro toto je uveden výše. Proto r = 2√3 (cm). Pak oblast kruhu: S = π * r ² = 3,14 * (2√3) ² = 37,68 (cm ² ).

Zbývá počítat objem: V = 37, 68 * 4 = 150,72 (cm ³ ).

Odpověď zní . V = 150,72 cm3.

Č. 2. Podmínka. Vypočítejte poloměr kruhu, který je napsán v pravém šestiúhelníku. Jeho strana je známá jako √ 3 cm. Jaký je jeho obvod rovný?

Rozhodnutí. Tento úkol vyžaduje použití dvou výše uvedených vzorců. A je třeba je aplikovat, a to i bez úpravy, jen nahradit hodnotu strany a vypočítat.

Poloměr zapsaného kruhu je tedy 1,5 cm. Pro obvod je tato hodnota pravdivá: 6,3 cm.

Odpověď zní. r = 1,5 cm, P = 6,3 cm.

Č. 3. Podmínka. Poloměr okruhu je 6 cm. Jaká je hodnota strany pravidelného šestiúhelníku v tomto případě?

Rozhodnutí. Z vzorce o poloměru, který je napsán v šestiúhelníku kruhu, lze snadno získat ten, který potřebujete k výpočtu strany. Je zřejmé, že poloměr je vynásoben dvěma a dělený kořenem tří. V jmenovateli je třeba zbavit iracionality. Výsledek akcí má tedy následující formu: (12 √3) / (√3 * √3), tj. 4√3.

Odpověď zní. a = 4,3 cm