Jaká je síla abecedy

Abeceda v oblasti počítačové vědy je systém signatury, pomocí něhož můžete předložit informační zprávu. Abychom porozuměli podstatě této definice, uvádíme několik dalších teoretických skutečností:

1. Všechny zprávy se skládají z abecedy. Tento článek je například zpráva. Pak se skládá z znaků ruské abecedy.
2. Pod symbolem rozumíme minimální významnou část abecedy. Také nedělitelné částice se nazývají atomy. Postavy v ruské abecedě jsou "a", pak "b", "c" a tak dále.
3. Teoreticky abeceda nemusí být zakódována žádným způsobem. Například v tištěné knize symboly abecedy znamenají, což znamená, že nemají žádné kódování.

Ale v praxi máme následující: počítač nechápe, co jsou dopisy. Proto k přenosu informační zprávy musí být nejprve zakódována v jazyce srozumitelném pro počítač. Abychom mohli pokračovat, je třeba zavést další podmínky.

Jaká je síla abecedy

Abecední mocí rozumíme celkový počet znaků v něm. Abyste zjistili, jaká je síla abecedy, stačí započítat počet znaků v něm. Zjistíme to. Pro ruskou abecedu je síla abecedy 33 nebo 32 znaků, pokud nepoužíváte "e".

Předpokládejme, že se všechny znaky v naší abecedě setkávají se stejnou pravděpodobností. Tento předpoklad lze chápat následovně: předpokládáme, že máme pytel s podepsanými kostkami. Počet kostek v něm je nekonečný a každý je podepsán pouze jedním symbolem. Pak s rovnoměrným rozdělením, bez ohledu na to, kolik krychlík vyjdeme ze sáčku, bude počet kostek s různými symboly stejný, nebo to bude mít tendenci s nárůstem počtu kostek, které vytáhneme z tašky.

Hodnocení váhy informačních zpráv

Téměř před sto lety získal americký inženýr Ralph Hartley vzorec, s nímž můžete hodnotit množství informací ve zprávě. Jeho vzorec pracuje na stejně pravděpodobných událostech a vypadá takto:

i = log ₂ M

Kde "i" je počet nedělitelných atomů informací (bity) ve zprávě, "M" je síla abecedy. Sledujeme. Pomocí matematických transformací můžeme určit, že síla abecedy lze vypočítat následovně:

M = 2 ⁱ

Tento vzorec obecně určuje souvislost mezi počtem stejně pravděpodobných událostí "M" a množstvím informací "i".

Vypočtěte výkon

S největší pravděpodobností už z kurzu počítačové vědy již víte, že v moderních výpočetních systémech postavených na architektuře von Neumanna se používá systém kódování binárních informací. Obě programy a data jsou kódovány tímto způsobem.

Aby bylo možné prezentovat text ve výpočetním systému, použijte jednotný kód osmi bitů. Kód je považován za jednotný, protože obsahuje pevnou sadu prvků - 0 a 1. Hodnoty v tomto kódu jsou specifikovány určitým pořadím těchto prvků. Pomocí osmibitového kódu můžeme kódovat zprávy o hmotnosti 256 bitů, protože pomocí vzorce Hartley: M ₈ = 2 ⁸ = 256 bitů informací.

Tato situace s kódováním znaků v binárním kódu se historicky vyvíjela. Ale teoreticky bychom mohli reprezentovat data jinými abecedami. Takže například ve čtyřpísmenné abecedě by každá postava měla váhu ne jeden, ale dva bity, v osmi znakové abecedě - 3 bity a tak dále. Vypočítá se pomocí výše uvedeného binárního logaritmu ( i = log ₂ M ).

Jelikož v abecedě s kapacitou 256 bitů je pro jeden znak přiděleno osm binárních čísel, bylo rozhodnuto o zavedení dodatečné míry informací - bajtů. Jeden byte obsahuje jeden znak tabulky kódů ASCII a obsahuje osm bitů.

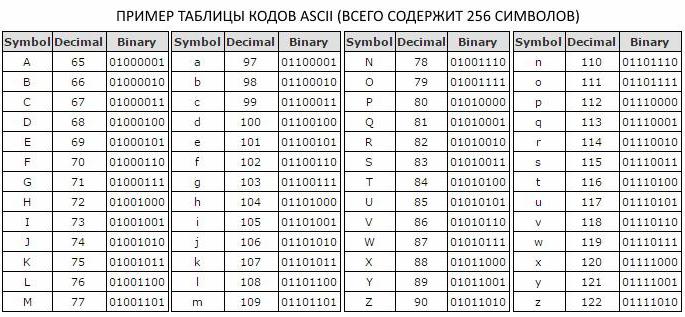
Jak měřit informace

в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы. Osmibitové kódování textových zpráv, které se používá v tabulce kódů ASCII, vám umožňuje vkládat základní sadu latinských a cyrilických znaků do malých a velkých písmen, čísel, interpunkčních znamének a dalších základních znaků.

Chcete-li měřit větší množství dat, použijte speciální předpony na slova byte a bit. Takové přílohy jsou uvedeny v následující tabulce:

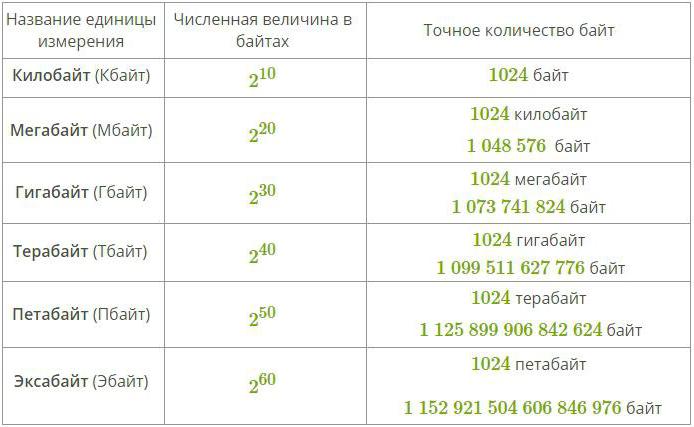
Mnoho lidí, kteří studovali fyziku, bude tvrdit, že by bylo rozumné používat klasické předčíslí pro označení jednotek informací (např. Kilo a mega), ale ve skutečnosti to není zcela správné, protože takové předpony hodnot označují násobení jedním nebo druhým stupněm deseti kdy se binární systém měření používá všude v informatice.

Správné názvy datových jednotek

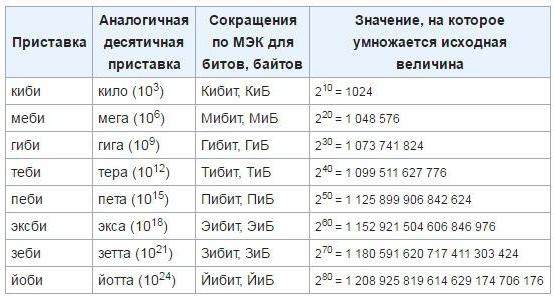
Za účelem odstranění nepřesností a nepříjemností schválila Mezinárodní komise pro elektrotechniku ​​v březnu 1999 nové jednotky, které se používají k určení množství informací v elektronické výpočetní technice. Takové předpony jsou "mebi", "kibi", "gibi", "tebi", "eksbi", "petit". Dosud se tyto jednotky ještě nezakopily, takže je nejpravděpodobnější, že je čas potřebný pro zavedení tohoto standardu a začátek rozšířeného používání. Jak provést přechod z klasických jednotek na nově schválené, můžete určit následující tabulku:

Předpokládejme, že máme text obsahující znaky K. Pak pomocí abecedního přístupu můžete vypočítat množství informací V, které obsahuje. Bude se rovnat výsledku síly abecedy o informaci o hmotnosti jednoho znaku v něm.

Pomocí vzorce Hartley víme, jak vypočítat množství informací pomocí binárního logaritmu. Za předpokladu, že počet znaků abecedy se rovná N a počet znaků v záznamu informační zprávy se rovná K, získáme následující vzorec pro výpočet objemu informací zprávy:

V = K ⋅ log ₂ N

Abecední přístup naznačuje, že objem informací bude záviset pouze na síle abecedy a na velikosti zpráv (tj. Počtu znaků v něm), ale v žádném případě nebude spojen se sémantickým obsahem pro osobu.

Příklady výpočtu výkonu

Ve třídě informatika často dává úkol najít sílu abecedy, délku zprávy nebo objem informací. Zde je jeden z těchto úkolů:

"Textový soubor zabírá 11 kB místa na disku a obsahuje 11264 znaků. Zjistěte sílu abecedy tohoto textového souboru."

Jaké bude řešení, můžete vidět na následujícím obrázku.

Abeceda o kapacitě 256 znaků tedy nese pouze 8 bitů informací, které se v počítačové vědě nazývají jeden byte. Bajt popisuje 1 znak tabulky ASCII, který, pokud o tom přemýšlíte, vůbec není hodně.

Je jeden byte hodně nebo málo?

Moderní sklady dat, jako jsou datová centra Google a Facebook, obsahují ne méně než desítky petabytů informací. Přesné množství dat však bude obtížné vypočítat samo od sebe, protože pak budete muset zastavit všechny procesy na serverech a blízké uživatele přístup k záznamu a úpravě svých osobních informací.

Abychom si však mohli představit takové nepředstavitelné množství dat, je třeba jasně pochopit, že vše je tvořeno malými detaily. Je nutné pochopit, jaká je abeceda (256) a kolik bitů obsahuje 1 bajt informací (jak si pamatujete, 8).