Základní pojmy teorie pravděpodobnosti a matematické statistiky

Matematika zahrnuje celou řadu oblastí, z nichž jedna, společně s algebrou a geometrií, je teorie pravděpodobnosti. Existují termíny, které jsou společné všem těmto oblastem, ale kromě nich existují specifické, zvláštní pouze pro jednu zvláštní "nika" slova, vzorce, věty.

Fráze "teorie pravděpodobnosti" způsobuje paniku v nepřipraveném studentovi. Fantazie nakonec vykresluje obrazy, kde se objevují hrozné volumetrické vzorce, a řešení jednoho problému zaujme celý notebook. V praxi to však není tak hrozné: postačí pochopit význam smluvních termínů a dostat se do jádra nějaké zvláštní logiky odůvodnění, aby se jednou a navždy přestala bát úkolů. V tomto ohledu považujeme základní pojmy teorie pravděpodobnosti a matematické statistiky - mladou, ale velmi zajímavou oblast znalostí.

Proč vyučovat koncepty

Funkcí jazyka je přenášet informace od jedné osoby k druhé tak, aby je chápal, uvědomil si a je schopen ji používat. Každý matematický koncept lze vysvětlit jednoduchými slovy, avšak v tomto případě by výměna dat vyžadovala mnohem více času. Představte si, že namísto slova "hypotenuse" byste vždy museli říkat "nejdelší strana pravého trojúhelníku" - to je velmi nepříjemné a dlouhé.

Proto lidé vymýšlejí nové pojmy pro určité jevy a procesy. Základní pojmy teorie pravděpodobnosti - událost, pravděpodobnost události apod. - se objevily stejným způsobem. Aby bylo možné používat vzorce, řešit problémy a aplikovat dovednosti v životě, je nutné nejen zapamatovat si nová slova, ale také pochopit, co každá z nich znamená. Čím hlubší si je uvědomujete, ponoříte se do významu, tím širší je rozsah vašich možností a čím víc vnímáte svět kolem vás.

Jaký je význam předmětu?

Seznámíme se se základními pojmy teorie pravděpodobnosti. Klasická definice pravděpodobnosti je následující: je to poměr výsledků, které odpovídají výzkumnému pracovníkovi, s celkovým počtem možných. Uveďme jednoduchý příklad: když člověk vyhodí zápěstí, může ztratit jednu ze šesti stran směrem nahoru. Celkový počet výsledků je tedy šest. Pravděpodobnost, že náhodně vybraná strana vypadne, je 1/6.

Schopnost předpovědět vznik určitého výsledku je pro různé specialisty nesmírně důležitá. Kolik chybných částí se očekává v hodně? Záleží na tom, kolik produkuje. Jaká je pravděpodobnost, že lék pomůže v boji proti nemoci? Tyto informace jsou zásadní. Ale nenechávejte čas na další příklady a pokračujte ke studiu nové oblasti pro nás.

První známý

Zvažte základní pojmy teorie pravděpodobnosti a jejich použití. In správně přírodní vědy, ekonomické vzorce a termíny uvedené níže jsou používány všude, protože přímo souvisejí se statistikami a chybami měření. Podrobnější studie této otázky vám otevře nové vzorce, které jsou užitečné pro přesnější a složitější výpočty, ale pojďme začít jednoduchým.

Jedním z nejzákladnějších a nejzákladnějších pojmů teorie pravděpodobnosti a matematické statistiky je náhodná událost. Vysvětlete jasnými slovy: ze všech možných výsledků experimentu je výsledkem jen jeden. I když je pravděpodobnost výskytu této události mnohem vyšší než druhá, bude to náhodná, protože teoreticky by výsledek mohl být jiný.

Pokud jsme provedli řadu experimentů a získali určitý počet výsledků, pravděpodobnost každého z nich se vypočítá pomocí vzorce: P (A) = m / n. Zde m je kolikrát jsme v testovacím seriálu viděli výsledek zájmu o nás. Na druhé straně je n celkový počet provedených experimentů. Pokud jsme hodili minci 10krát a dostali "ocasy" 5krát, pak m = 5 a n = 10.

Typy událostí

Stává se, že určitý výsledek je zaručen v každém pokusu - taková událost se nazývá spolehlivá. Pokud se to nikdy nestane, bude to nazýváno nemožné. Takové události se však nepoužívají v podmínkách problémů s teorií pravděpodobnosti. Základní pojmy, které je mnohem důležitější znát, jsou společné a nekompatibilní události.

Stává se, že během experimentu nastávají současně dvě události. Například rotujeme dvě kostky - v tomto případě skutečnost, že jeden "šest" vypadl, nezaručuje, že druhá nespadne na druhou. Takové události se nazývají společné.

Pokud zahájíme jeden zemřít, pak dvě čísla současně nebudou moci vypadnout vůbec. V tomto případě budou výsledky ve formě "jednoho", "dvou" atd. Považovány za nekompatibilní události. Je velmi důležité rozlišit, které výsledky se odehrávají v každém konkrétním případě - záleží na tom, které vzorce použijeme při hledání problému. Základní pojmy teorie pravděpodobnosti budeme i nadále zkoumat několik odstavců později, když budeme zvažovat vlastnosti přidání a násobení. Bez nich, žádný problém nelze vyřešit.

Množství a produkt

Předpokládejme, že uděláš zemřít s kamarádem a že má "čtyři". Musíte získat pět nebo šest vyhrát. V takovém případě budou pravděpodobnosti shrnuty: protože pravděpodobnost, že obě čísla budou vypadnuta, bude 1/6, odpověď bude vypadat jako 1/6 + 1/6 = 1/3.

Představte si, že dvakrát udeříte a váš přítel dostal 11 bodů. Nyní musíte mít "šest" dvakrát za sebou. Události jsou navzájem nezávislé, proto je třeba vynásobit pravděpodobnost: 1/6 * 1/6 = 1/36.

Mezi základní pojmy a teorémy teorie pravděpodobnosti je třeba věnovat pozornost součtu pravděpodobností společných událostí, t. to znamená ty, které se mohou vyskytnout současně. Vzorec přidání v tomto případě vypadá takto: P (A + B) = P (A) + P (B) - P (AB).

Kombinatorika

Velmi často musíme najít všechny možné kombinace některých parametrů objektu nebo vypočítat počet všech kombinací (například při výběru šifry). Kombinatorika, která úzce souvisí s teorií pravděpodobnosti, nám v tom pomůže. Základní pojmy zde obsahují několik nových slov a řada vzorců z tohoto tématu jistě přijde vhod.

Předpokládejme, že máte tři čísla: 1, 2, 3. Potřebujete je použít, abyste napsali všechna možná třímístná čísla. Kolik bude? Odpověď: n! (vykřičník znamená faktoriální). Kombinace řady různých prvků (čísla, písmena atd.), Které se liší pouze v pořadí jejich umístění, se nazývají permutace.

Častěji se však setkáváme s takovou situací: 10 číslic (od nuly do devět), z nichž je složeno heslo nebo kód. Předpokládejme, že délka je 4 znaky. Jak vypočítat celkový počet možných kódů? K tomu existuje speciální vzorec: (n!) / (N - m)!

Vzhledem k výše uvedenému problému, n = 10, m = 4. Dále jsou zapotřebí pouze jednoduché matematické výpočty. Mimochodem, takové kombinace se nazývají umístění.

Konečně existuje koncept kombinací - jde o sekvence, které se navzájem liší alespoň jedním prvkem. Jejich počet je vypočten podle vzorce: (n!) / (M! (Nm)!).

Matematické očekávání

Důležitým pojetím, se kterým se student setkává již v prvních třídách, je matematické očekávání. Je součtem všech možných hodnot výsledku vynásobených jejich pravděpodobnostmi. V podstatě je to průměrné číslo, které můžeme předpovědět jako výsledek testu. Například existují tři hodnoty, pro které pravděpodobnosti jsou uvedeny v závorkách: 0 (0,2); 1 (0,5); 2 (0,3). Vypočtěte očekávání: M (X) = 0 * 0,2 + 1 * 0,5 + 2 * 0,3 = 1,1. Z navrhovaného výrazu tedy vidíme, že tato hodnota je konstantní a nezávisí na výsledku testu.

Tento koncept je používán v mnoha formulech a opakovaně se s ním setkáte v budoucnu. S ním je snadné pracovat: očekávání součtu se rovná součtu rohožky. očekávání - M (X + Y) = M (X) + M (Y). Totéž platí pro produkt: M (XY) = M (X) * M (Y).

Disperze

Musí být z kurzu fyziky školy, že si pamatujete, že rozptyl je rozptýlen. Jaké je místo mezi základními pojmy teorie pravděpodobnosti?

Podívejte se na dva příklady. V jednom případě dostaneme: 10 (0,2); 20 (0,6); 30 (0,2). V druhé - 0 (0,2); 20 (0,6); 40 (0,2). Matematické očekávání bude v obou případech stejné, jak tedy můžeme porovnat tyto situace? Koneckonců vidíme pouhým okem, že šíření hodnot v druhém případě je mnohem větší.

Za tímto účelem byla zavedena koncepce rozptylu. Chcete-li to získat, musíte vypočítat očekávání součtu rozdílů každé náhodné proměnné a očekávání. Vezměte si čísla z prvního příkladu zaznamenaného v předchozím odstavci.

Nejprve vypočítáme očekávání: M (X) = 10 * 0,2 + 20 * 0,6 + 30 * 0,2 = 20. Pak hodnota rozptylu: D (X) = 40.

Další ze základních pojmů statistik a teorie pravděpodobnosti je standardní odchylka. Vypočítejte, že je to velmi jednoduché: stačí jen vzít druhá odmocnina z disperze.

Zde můžeme zaznamenat takový jednoduchý termín, jako rozsah. Tato hodnota označuje rozdíl mezi maximální a minimální hodnotou ve vzorku.

Statistiky

Některé koncepty základní školy jsou používány ve vědě velmi často. Dvě z nich jsou aritmetický průměr a medián. Určitě si vzpomenete, jak najít jejich hodnoty. Ale jen pro případ, připomínáme: aritmetický průměr je součet všech hodnot dělených jejich počtem. Pokud je hodnota 10, pak je přidáme a rozdělíme o 10.

Střední je pro všechny možné. Pokud máme lichý počet hodnot, pak je napíšeme vzestupně a vybereme ten, který byl uprostřed. Pokud máme párný počet hodnot, vezmeme dva centrální a dělíme dva.

Dvě další hodnoty, které se nacházejí mezi střední hodnotou a dvěma extrémními - maximálními a minimálními hodnotami sady, se nazývají kvartilie. Jsou vypočteny stejným způsobem - s lichým počtem prvků, je přijato číslo, které je umístěno ve středu řádku, a pro sudé - polovinu součtu dvou centrálních prvků.

Existuje také speciální graf, ve kterém můžete vidět všechny hodnoty vzorku, jeho rozsah, medián, mezičtvrtletní interval, stejně jako odlehlé hodnoty, které neodpovídají statistické chybě. Výsledný obraz má velmi specifické (a dokonce i matematické) jméno - krabici s knírem.

Distribuce

Distribuce také odkazuje na základní pojmy teorie pravděpodobnosti a matematické statistiky. Stručně řečeno, je to shrnutí všech náhodných proměnných, které můžeme vidět jako výsledek testu. Hlavním parametrem je pravděpodobnost výskytu každé konkrétní hodnoty.

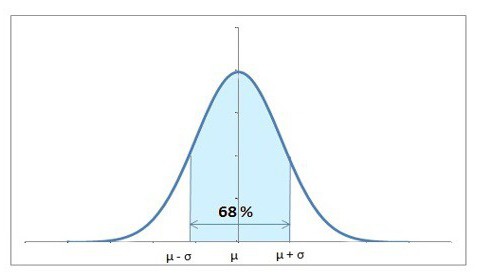Normální distribuce je taková, která má jeden středový vrchol, ve kterém se nejčastěji nachází nejvyšší hodnota. Z jeho oblouků se liší méně a méně pravděpodobné výsledky. Obecně platí, že plán z boku vypadá jako "snímek". V budoucnu se dozvíte, že ústřední limitní věta, která je základem teorie pravděpodobnosti, je úzce spojena s tímto typem distribuce. Popisuje zákony, které jsou důležité pro zamýšlené oblasti matematiky, které jsou velmi užitečné pro různé výpočty.

Ale zpět k tématu. Existují ještě dva typy distribucí: asymetrické a multimodální. První z nich vypadá jako polovina "normálního" grafu, tj. Oblouk jde dolů pouze v jednom směru od špičkové hodnoty. Konečně, multimodální distribuce je taková, která má několik "horních" hodnot. Rozvrh pak padá, pak se zvedne. Nejvíce frekvenční hodnota v libovolné distribuci se nazývá režim. Je také jedním ze základních pojmů teorie pravděpodobnosti a matematické statistiky.

Gaussova distribuce

Gaussovo nebo normální rozdělení je takové, v němž se odchylka pozorování od středu řídí určitým zákonem.

Stručně řečeno, hlavní rozptyl vzorkových hodnot exponenciálně směřuje k režimu - nejčastější z nich. Přesněji řečeno, pak 99,6% všech hodnot spočívá ve třech standardních odchylkách (nezapomeňte, že jsme se na tuto koncepci podívali výše?).

Gaussova distribuce je jedním ze základních pojmů teorie pravděpodobnosti. S pomocí toho je možné pochopit, zda je prvek zařazen do kategorie "typický" podle jednoho nebo jiného parametru - tak je výška a váha člověka hodnocena podle věku, úrovně intelektuálního vývoje, psychického stavu a mnohem více.

Jak požádat

Je zajímavé, že "nudné" matematické údaje lze využít ve svůj prospěch. Například jeden mladík použil teorii pravděpodobnosti a statistiky, aby získal několik milionů dolarů v ruletě. Je pravda, že jsme se na to museli připravit - v průběhu několika měsíců jsme zaznamenali výsledky her v různých kasinech.

Po analýze zjistil, že jedna z tabulek je mírně nakloněná, což znamená, že se řada hodnot objevuje statisticky významně častěji než ostatní. Jen málo výpočtů, trpělivost - a nyní majitelé instituce jsou zmateni, přemýšleli, jak může člověk mít štěstí.

Existuje spousta běžných každodenních úkolů, které nelze vyřešit bez použití statistiky. Například, jak zjistit, kolik obchodů objednat oblečení různých velikostí: S, M, L, XL? K tomu je třeba analyzovat, kdo často kupuje oblečení ve městě, v oblasti, v nedalekých obchodech. Pokud takové informace nejsou získány, majitel riskuje ztrátu velkého množství peněz.

Závěr

Podívali jsme se na celou řadu základních pojmů teorie pravděpodobnosti: test, událost, permutace a umístění, očekávání a rozptyl, móda a normální rozdělení ... Kromě toho jsme zkoumali řadu vzorců, na něž byl věnován více než měsíc studie.

Nezapomeňte: matematika je nezbytná při studiu ekonomie, přírodních věd, informačních technologií, inženýrských oborů. Statistiky jako jedna ze svých oblastí zde nelze vyhnout.

Teď je na vás: cvičit, vyřešit problémy a příklady. Dokonce i základní pojmy a definice teorie pravděpodobnosti budou zapomenuty, ne-li věnovat čas opakování. Navíc následující vzorce se do značné míry spoléhají na ty, které jsme uvažovali. Proto se je snažte zapamatovat, zejména proto, že není mnoho z nich.