Korelační koeficient a příčinný vztah: vzorce a jejich interpretace
Korelační koeficient je stupeň spojení mezi dvěma proměnnými. Jeho výpočet dává představu o tom, zda existuje závislost mezi dvěma datovými poli. Na rozdíl od regrese korelace neumožňuje předpovídat hodnoty veličin. Výpočet koeficientu je však důležitým krokem v předběžné statistické analýze. Zjistili jsme například, že korelační koeficient mezi úrovní přímých zahraničních investic a tempem růstu HDP je vysoký. To nám dává představu, že pro zajištění dobrých životních podmínek je nutné vytvořit příznivé klima specifické pro zahraniční podnikatele. Ne tak zřejmý závěr na první pohled!
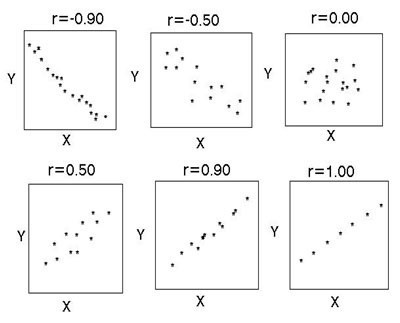
Korelace a příčinná souvislost
Snad neexistuje žádná oblast statistiky, která by byla v našem životě tak pevně stanovena. Korelační koeficient se používá ve všech oblastech veřejného poznání. Jeho hlavní nebezpečí spočívá v tom, že jeho vysoké hodnoty jsou často spekulovány, aby přesvědčily lidi a učinily je věřit v některé závěry. Ve skutečnosti však silná korelace vůbec nevypovídá o kauzálním vztahu mezi množstvím.
Korelační koeficient: formula Pearson a Spearman
Existuje několik klíčových indikátorů, které charakterizují vztah mezi dvěma proměnnými. Historicky první je lineární korelační koeficient Pearson. Je ještě ve škole. Vyvinula ji C. Pearson a J. Yul na základě prací Fr. Galton. Tento koeficient vám umožňuje vidět vztah mezi racionálními čísly, které se racionálně mění. Je vždy větší než -1 a menší než 1. Záporné číslo znamená nepřímo poměrnou závislost. Pokud je koeficient nula, pak mezi proměnnými neexistuje žádné spojení. Stejně jako kladné číslo - mezi studovanými veličinami existuje přímo poměrný vztah. Spearmanův korelační koeficient vám umožňuje zjednodušit výpočty budováním hierarchie proměnných hodnot.
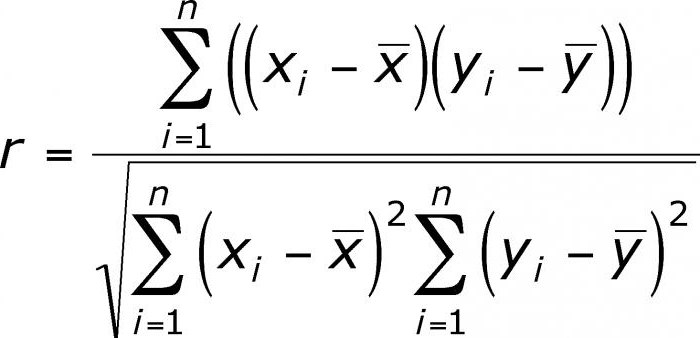
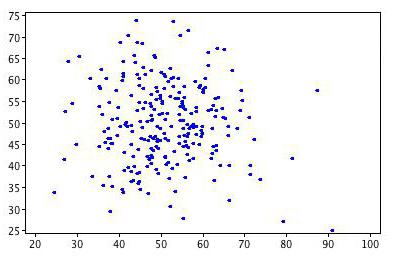
Vztah mezi proměnnými
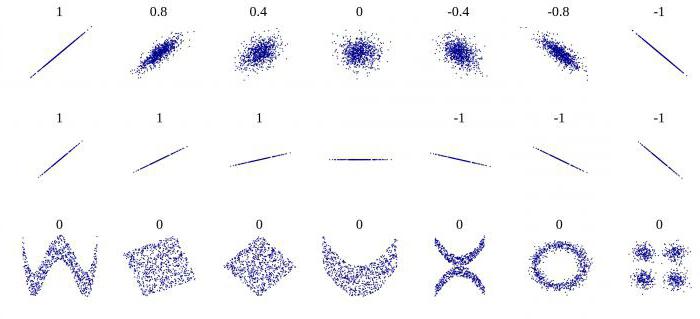
Korelace pomáhá najít odpověď na dvě otázky. Za prvé, vztah mezi proměnnými je pozitivní nebo negativní. Za druhé, jak silná je závislost. Korelační analýza je mocným nástrojem, pomocí kterého můžete získat tyto důležité informace. Je snadné vidět, že příjmy a výdaje rodiny klesají a rostou proporcionálně. Tento vztah je považován za pozitivní. Naopak, s růstem cen zboží, poptávka po ní klesá. Takové spojení se nazývá negativní. Hodnoty korelačního koeficientu jsou v rozmezí od -1 do 1. Zero znamená, že neexistuje žádný vztah mezi hodnotami, které jsou předmětem studie. Čím blíže je indikátor k extrémním hodnotám, tím silnější je spojení (negativní nebo pozitivní). Absence závislosti je indikována koeficientem od -0,1 do 0,1. Je třeba si uvědomit, že taková hodnota označuje pouze nepřítomnost lineárního spojení.
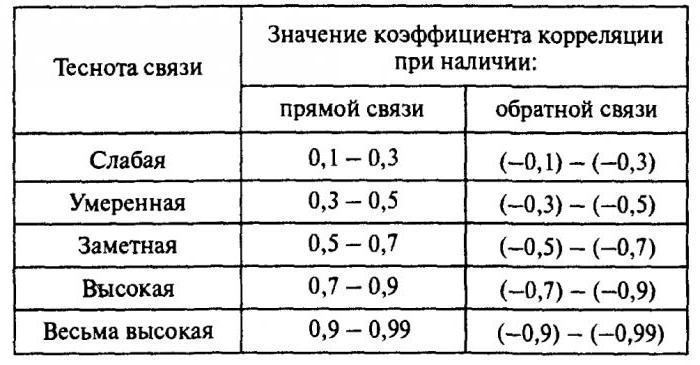
Funkce aplikace
Použití obou ukazatelů podléhá určitým předpokladům. Za prvé, přítomnost silného spojení neznamená skutečnost, že jedno množství určuje jiné. Může se jednat o třetí množství, které definuje každou z nich. Za druhé, vysoký korelační koeficient Pearson neindikuje kauzální vztah mezi sledovanými proměnnými. Zatřetí ukazuje pouze lineární závislost. Korelace může být použita k odhadu významných kvantitativních dat (například atmosférický tlak, teplota vzduchu) a nikoliv kategorie, jako je pohlaví nebo oblíbená barva.
Více koeficient korelace
Pearson a Spearman zkoumali vztah mezi těmito dvěma proměnnými. Ale jak jednat v případě, že jsou tři nebo dokonce více. Zde dochází k záchraně vícenásobného korelačního koeficientu. Například hrubý národní produkt není ovlivňován pouze přímým zahraniční investice ale také měnovou a fiskální politiku státu, stejně jako úroveň vývozu. Rychlost růstu a objem HDP jsou výsledkem vzájemného působení řady faktorů. Mělo by však být zřejmé, že model vícečetné korelace je založen na řadě zjednodušení a předpokladů. Za prvé je vyloučena vícenásobnost mezi jednotlivými veličinami. Za druhé, vztah mezi závislou a proměnnými, která ji ovlivňují, se předpokládá lineární.
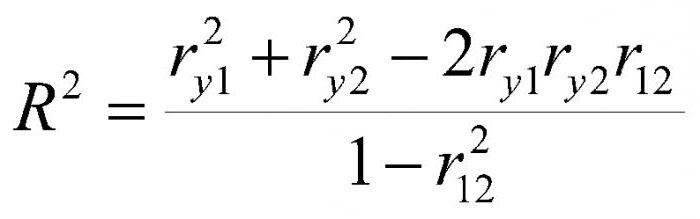
Oblasti použití korelační a regresní analýzy
Tato metoda nalezení vztahu mezi veličinami je široce používána ve statistikách. To je nejčastěji využíváno ve třech hlavních případech:
- Testovat příčinný vztah mezi hodnotami dvou proměnných. V důsledku toho se výzkumník snaží nalézt lineární vztah a odvodit vzorec, který popisuje tyto vztahy mezi veličinami. Jednotky jejich měření mohou být různé.
- Kontrola spojení mezi hodnotami. V tomto případě nikdo neurčuje, která proměnná je závislá. Může se ukázat, že hodnota obou veličin způsobuje jiný faktor.
- Odvodit rovnici. V tomto případě můžete jednoduše nahradit čísla v něm a zjistit hodnoty neznámé proměnné.
Člověk hledá příčinu
Vědomí je uspořádáno takovým způsobem, že rozhodně potřebujeme vysvětlit události, které se dějí kolem. Osoba vždy hledá spojení mezi obrazem světa, ve kterém žije, a informacemi, které přijímá. Často mozek vytváří pořádek z chaosu. Může snadno vidět příčinný vztah tam, kde není žádný. Vědci se musí zvláště naučit překonat tento trend. Schopnost vyhodnotit vztah mezi údaji je objektivně nutná v akademické kariéře.
Media zkreslení
Zvažte, jak může být nesprávně interpretována přítomnost korelačního odkazu. Skupina britských studentů se špatným chováním byla požádána, zda jejich rodiče kouřili. Test byl zveřejněn v novinách. Výsledek ukázal silnou korelaci mezi kouřením rodičů a přestupekmi jejich dětí. Profesor, který studium provedl, dokonce navrhl upozornění na balení cigaret. Existuje však řada problémů s tímto závěrem. Zaprvé korelace neukazuje, která z množství je nezávislá. Proto lze předpokládat, že závislost rodičů je způsobena neposlušností dětí. Zadruhé, nelze s jistotou říci, že oba problémy se neobjevily kvůli nějakému třetímu faktoru. Například rodiny s nízkými příjmy. Mělo by se poznamenat emoční aspekt počátečních zjištění profesora, který studii provedl. Byl to horlivý oponent kouření. Proto není divu, že tímto způsobem interpretoval výsledky svého výzkumu.
Závěry
Nesprávná interpretace korelace jako kauzálního vztahu mezi dvěma proměnnými může způsobit hanebné chyby ve výzkumu. Problém spočívá v tom, že leží v samém jádru lidského vědomí. Mnoho marketingových triků je postaveno na této konkrétní funkci. Pochopení rozdílu mezi příčinami a korelací umožňuje racionální analýzu informací jak v každodenním životě, tak v profesionální kariéře.