Denník geometrického postupu: vzorce a vlastnosti

Geometrický postup spolu s aritmetikou je důležitou číselnou řadou, která je studována v kurzu algebry v 9. ročníku. V tomto článku považujeme jmenovatele geometrického postupu a jak jeho hodnota ovlivňuje jeho vlastnosti.

Definice postupu geometrického

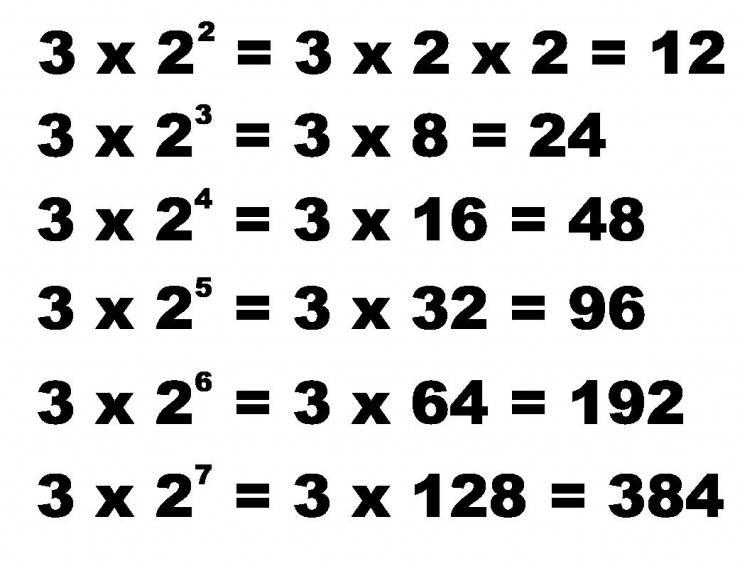
Nejprve uvádíme definici této číselné řady. Taková řada racionálních čísel, která je tvořena postupným znásobením prvního prvku konstantním číslem, nazývaným jmenovatelem, se nazývá geometrická progrese.

Například čísla v řádku 3, 6, 12, 24, ... je geometrická progrese, protože pokud násobíme 3 (první prvek) o 2, získáme 6. Pokud je 6 násobeno 2, dostaneme 12 a tak dále.

Členové posuzované sekvence jsou obvykle označeni symbolem a _i , kde i je celé číslo udávající číslo prvku v sérii.

Výše uvedená definice postupu může být zapsána v jazyce matematiky takto: a _n = b ^n-1 * a ₁ , kde b je jmenovatel. Je snadné zkontrolovat tento vzorec: jestliže n = 1, pak b ^1-1 = 1 a my dostaneme ₁ = a _1. Pokud n = 2, pak _n = b * a ₁ a opět se dostaneme k definici zvážené řady čísel . Podobné argumenty mohou pokračovat pro velké hodnoty n.

Menovec progrese geometrického

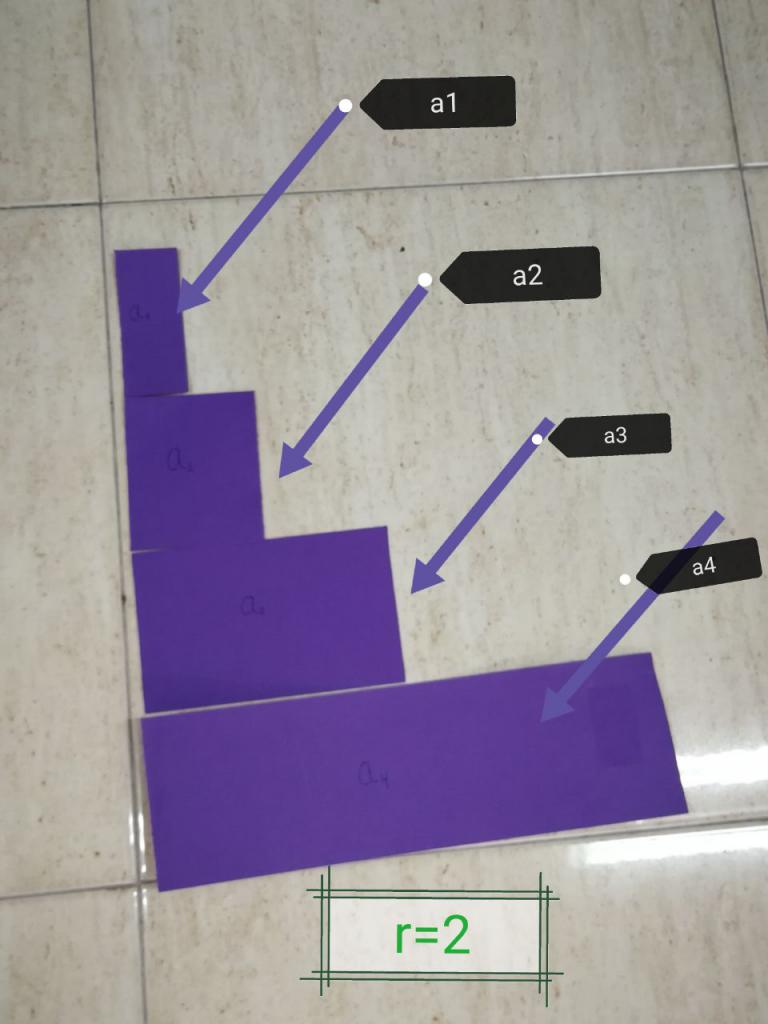
Číslo b zcela určuje povahu celé série čísel. Denominátor b může být pozitivní, negativní a také má hodnotu větší než jeden nebo méně. Všechny tyto možnosti vedou k různým sekvencím:

• b> 1. Existuje rostoucí počet racionálních čísel. Například 1, 2, 4, 8, ... Pokud je prvek a ₁ záporný, celá posloupnost se zvýší pouze v absolutní hodnotě, ale snižuje se vzhledem k znamení čísel.
• b <-1. V tomto případě mluvíme o proměnné sérii, to znamená, že sousední prvky se budou lišit v označení. Například 1, -2, 4, -8, 16, ...
• -1 <b <1. Jedná se o speciální případ, který má své vlastní jméno - klesající nekonečný geometrický postup. Jeho hlavní rys je, že bez ohledu na znamení jmenovatele má tendenci k určitému konečnému součtu, když přidává nekonečný počet jeho prvků.
• b = 1. Často se takový případ nazývá progrese, neboť existuje obvyklá série identických racionálních čísel. Například -4, -4, -4.

Vzorec pro součet

Předtím, než začneme zvažovat konkrétní úkoly s použitím jmenovatele daného typu progrese, je třeba uvést důležitý vzorec pro součet jeho prvních n prvků. Vzorec má formu: S _n = (b ⁿ - 1) * a ₁ / (b - 1).

Tento výraz můžete získat sami, pokud považujete rekurzivní posloupnost členů progrese. Všimněte si také, že ve výše uvedeném vzorci stačí znát pouze první prvek a jmenovatele, aby našel součet libovolného počtu členů.

Nekonečně klesající posloupnost

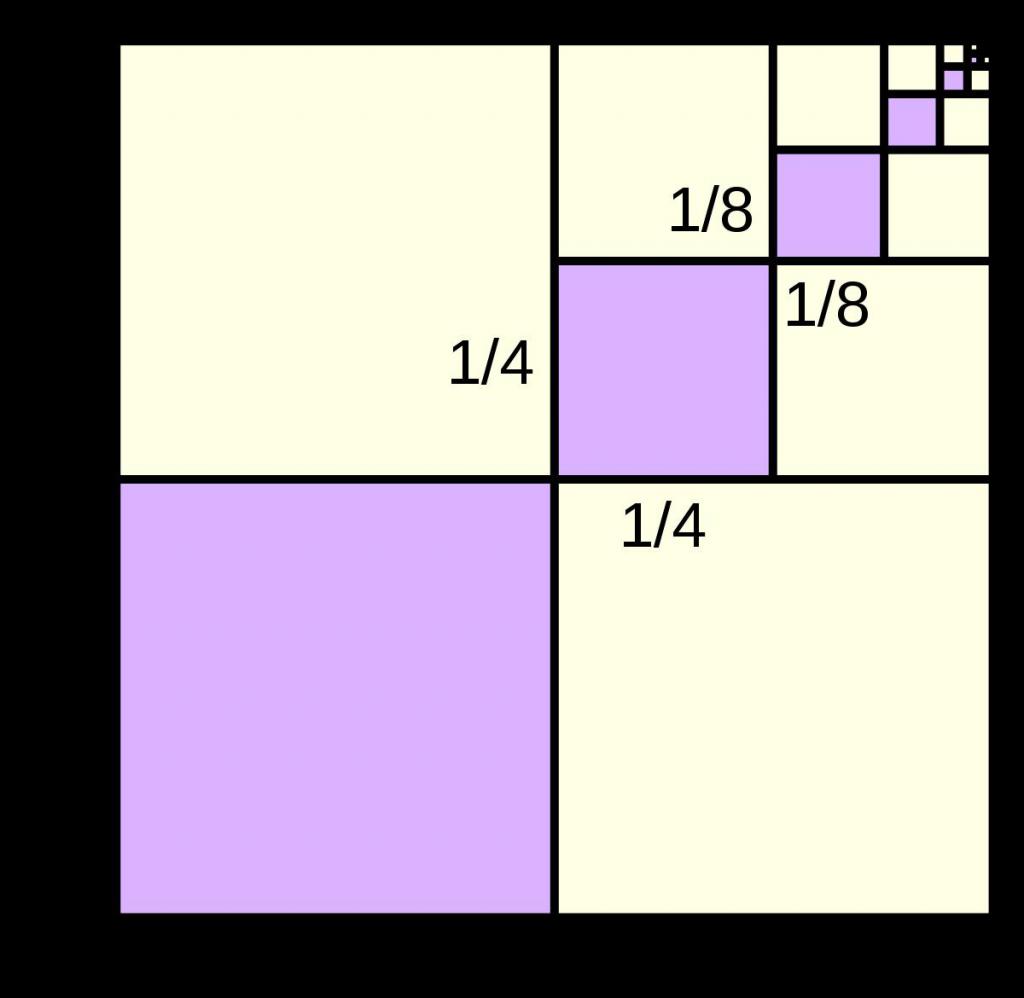
Nahoře bylo vysvětleno, co to je. Nyní, znát vzorec pro S _n , aplikujte jej na tuto číselnou řadu. Protože libovolný počet, jehož modul nepřesahuje hodnotu 1, má tendenci k nulové hodnotě, když je stavěn na velké stupně, tj. B ^∞ => 0, pokud -1 <b <1 (| b | <1), potom se obecný vzorec pro součet převede na následující výraz: S _∞ = a ₁ / (1 - b).

Vzhledem k tomu, že rozdíl (1 - b) bude vždy pozitivní, bez ohledu na hodnotu jmenovatele, znamení součtu klesající nekonečné progrese geometrického S _{∞ je} jednoznačně určeno znaménkem prvního prvku a ₁ .

Nyní budeme uvažovat o několika úkolech, kde ukážeme, jak aplikovat znalosti získané z konkrétních čísel.

Číslo problému 1. Výpočet neznámých prvků postupu a množství

Vzhledem k postupu geometrického je jmenovatel progrese 2 a jeho první prvek 3. Co se bude rovnat jeho 7. a 10. členům a jaký je součet jeho sedmi počátečních prvků?

Podmínka problému je dost jednoduchá a zahrnuje přímé použití výše uvedených vzorců. Takže pro výpočet prvku s číslem n použijeme výraz a _n = b ^n-1 * a ₁ . Pro 7. prvek máme: a ₇ = b ⁶ * a _1, nahrazující známá data, dostaneme: a ₇ = 2 ⁶ * 3 = 192. Pro 10. člen postupujeme stejným způsobem: ₁₀ = 2 ⁹ * 3 = 1536 .

Pro sumu používáme dobře známý vzorec a určujeme tuto hodnotu pro prvních 7 prvků série. Máme: S ₇ = (2 ⁷ - 1) * 3 / (2 - 1) = 381.

Číslo problému 2. Určení součtu libovolných prvků postupu

Let -2 se rovná jmenovateli postupu v geometrické progresi b ^n-1 * 4, kde n je celé číslo. Je nutné stanovit částku od 5. do 10. prvku této řady včetně.

Problém, který představuje, nelze vyřešit přímo pomocí známých vzorců. Lze jej vyřešit dvěma různými způsoby. Pro úplnost udělíme obě.

Metoda 1. Její nápad je jednoduchý: je nutné vypočítat dvě odpovídající částky prvních členů a poté odečíst jeden od druhého. Vypočítáme menší část: S ₁₀ = ((-2) ¹⁰ - 1) * 4 / (-2 - 1) = -1364. Nyní vypočítáme velké množství: S ₄ = ((-2) ⁴ - 1) * 4 / (-2 - 1) = -20. Všimněte si, že v posledním výrazu byly shrnuty pouze 4 termíny, protože pátý je již zahrnut do součtu, který má být vypočítán podmínkou problému. Konečně učinit rozdíl: S ₅ ¹⁰ = S ₁₀ - S ₄ = -1364 - (-20) = -1344.

Metoda 2. Předtím, než nahradíte čísla a počítáte, můžete získat vzorec pro součet mezi členy m a n řady zvažovaných. Jednáme se stejným způsobem jako v metodě 1, pracujeme pouze s symbolickou reprezentací součtu. Máme: S ⁿ _m = (b ⁿ - 1) * a ₁ / (b - 1) - (b ^m-1 - 1) ¹ ) / (b-1). Do výsledného výrazu můžete nahradit známé čísla a vypočítat konečný výsledek: S ¹⁰ ₅ = 4 * ((-2) ¹⁰ - (-2) ⁴ ) / (-2 - 1) = -1344.

Číslo problému 3. Jaký je jmenovatel?

Nechť ₁ = 2, najdeme jmenovatele postupu geometrického, za předpokladu, že jeho nekonečný součet je 3 a je známo, že jde o klesající řadu čísel.

Podmínkou problému není těžké odhadnout, který vzorec by měl být použit k jeho vyřešení. Samozřejmě, že součet postupu je nekonečně klesající. Máme: S _∞ = a ₁ / (1 - b). Z toho vyjádíme jmenovatele: b = 1 - a ₁ / S _∞ . Zbývá nahradit známé hodnoty a získat požadované číslo: b = 1 - 2/3 = -1 / 3 nebo -0.333 (3). Tento výsledek je možné zkontrolovat kvalitativně, pokud si připomíme, že pro tento typ sekvence modul b nesmí překročit hodnotu 1. Jak je vidět, | -1 / 3 | <1.

Číslo problému 4. Obnova řady čísel

Nechte dát 2 prvky číselné řady, například 5. je 30 a 10. je 60. Je nutné rekonstruovat celou sérii z těchto dat, protože je známo, že splňuje vlastnosti geometrického postupu.

K vyřešení problému je zapotřebí zapsat odpovídající výraz pro každý známý člen. Máme: ₅ = b ⁴ * a ₁ a ₁₀ = b ⁹ * a ₁ . Nyní rozdělíme druhý výraz na první, získáme: a ₁₀ / a ₅ = b ⁹ * a ₁ / (b ⁴ * a ₁ ) = b ⁵ . Z tohoto důvodu určujeme jmenovatele, přičemž kořen pátého stupně z poměru známých výrazů k prohlášení o problému b = 1.148698 Výsledné číslo je nahrazeno jedním z výrazů pro známý prvek, dostaneme: a ₁ = a ₅ / b ⁴ = 30 / (1,148698) ⁴ = 17,2304966.

Zjistili jsme tedy, jaký je jmenovatel progrese bn, a geometrický průběh b ^n-1 * 17,2304966 = a _n , kde b = 1,148698.

Kde se uplatňuje geometrická progrese?

Pokud by tato čísla nebyla v praxi uplatněna, pak by se její studie omezila na čistě teoretický zájem. Taková aplikace však existuje.

Následují tři nejznámější příklady:

• Paradox Zenona, ve kterém smutný Achilles nedokáže zpomalit pomalou želvu, je vyřešen pomocí konceptu snižující se nekonečné řady čísel.
• Pokud na každé buňce šachovnice umístíte zrnka pšenice, vložte 1 zrnku na první buňku, 2 na druhou, 2 a 3 na třetí, pak potřebujete 18446744073709551615 zrní na vyplnění všech buněk desky!
• Ve hře "Tower of Hanoi", aby bylo uspořádání disků z jedné tyče do druhé, je třeba provést 2 ⁿ - 1 operace, tj. Jejich počet se exponenciálně zvyšuje s počtem použitých disků n.