Dynamika a kinematika kruhového pohybu: vzorce a řešení typického problému

Schopnost popsat pohyb v kruhu je důležitá pro výpočet technických vlastností rotačních hřídelí a ozubených kol. Tento typ pohybu se nachází také v každodenním životě a přírodě, jako je například rotace planet kolem slunce a bruslařů během vystoupení na sportovních soutěžích. V tomto článku budeme uvažovat o tom, jak z pohledu fyziky lze tento druh pohybu popsat.

Dynamika rotace

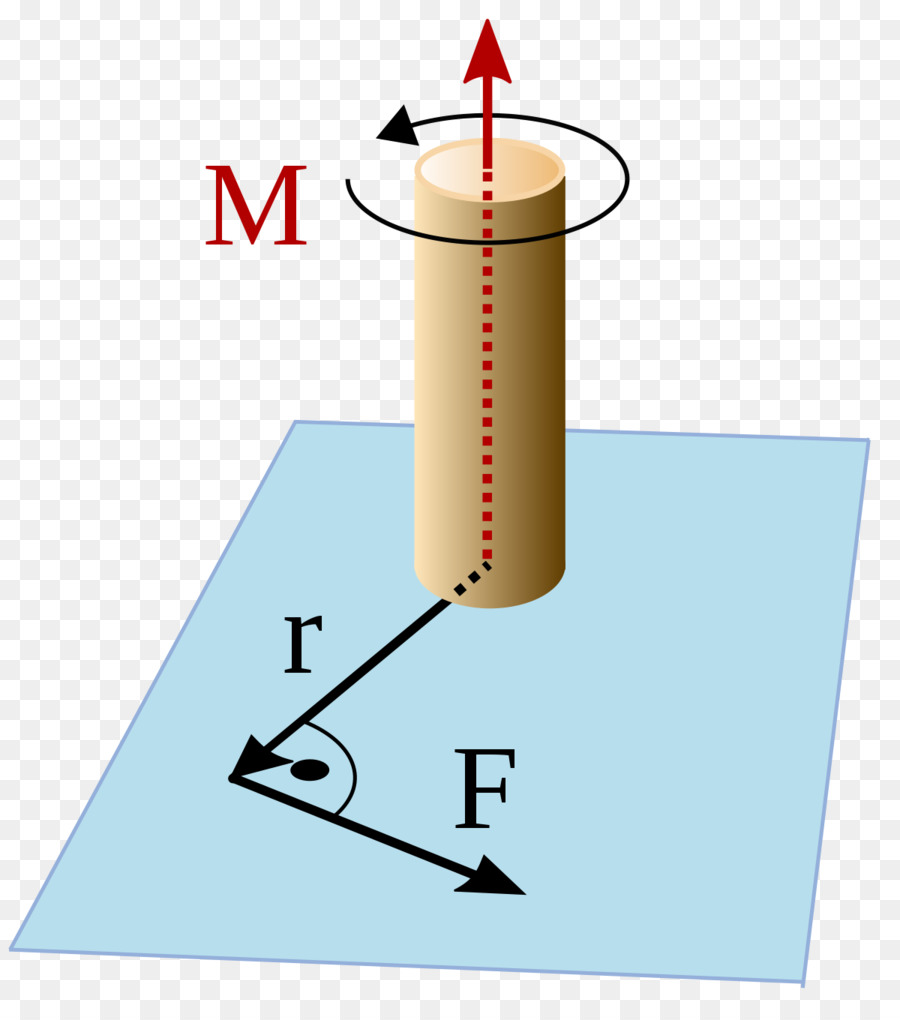
Pohyb v kruhu je rotace určitého těla nebo materiálového bodu kolem osy. Aby tělo mohlo začít otáčet, je nutné mít na daném systému vnější točivý moment. Tento okamžik je určen podle vzorce:

M = F * d

Zde F je síla, d je délka páky (vzdálenost mezi osou a bodem působení síly). Moment síly je vektorová hodnota. Vzorec se používá k výpočtu modulu M.

Vliv momentu M se na systém projeví v podobě vzhledu úhlové akcelerace. To znamená, že se systém začne otáčet. Hlavní vzorec pro kruhový pohyb je napsán jako:

M = I * α

Zde je moment setrvačnosti, α je úhlové zrychlení. Obě veličiny mají jejich analogy pro lineární případ. Pokud je všechno jasné s analogou hodnoty α, pak je třeba pro okamžik setrvačnosti I objasnit. Hodnota I odráží inerciální vlastnosti rotujícího systému. To znamená, že během rotace hraje stejnou roli jako obyčejná tělesná hmotnost.

Všimněte si, že výše uvedený výraz je analogií druhého zákona Newtona pro rotaci.

Centrifetální a odstředivé síly, zrychlení

Proces rotace znamená přítomnost určité vnitřní síly, která zajistí křivočarý pohyb těla. Tato síla se nazývá centripetální. Podle jména je vždy nasměrován z těla na osu rotace. Jelikož délka páky d je nulová, nevede k úhlovému zrychlení α. Nicméně mění vektor lineární rychlosti, to znamená, že vytváří zrychlení.

Zrychlení při pohybu v kruhu bez změny modulu lineární rychlosti se nazývá centripetální. Vypočítá se podle vzorce:

a _c = v2 / r

Kde v je lineární rychlost bodu materiálu rotující ve vzdálenosti r od osy.

Kromě centrifugace se často můžete dozvědět o odstředivé síle. Ta se snaží vyvést tělo z kruhové dráhy do přímky. Důvodem jeho vzniku jsou inerční vlastnosti rotujícího systému.

Při pohybu v kruhu jsou odstředivé a odstředivé síly stejné velikosti v sobě navzájem a ve směru, které jsou protilehlé.

Kinematické rovnice otáčení

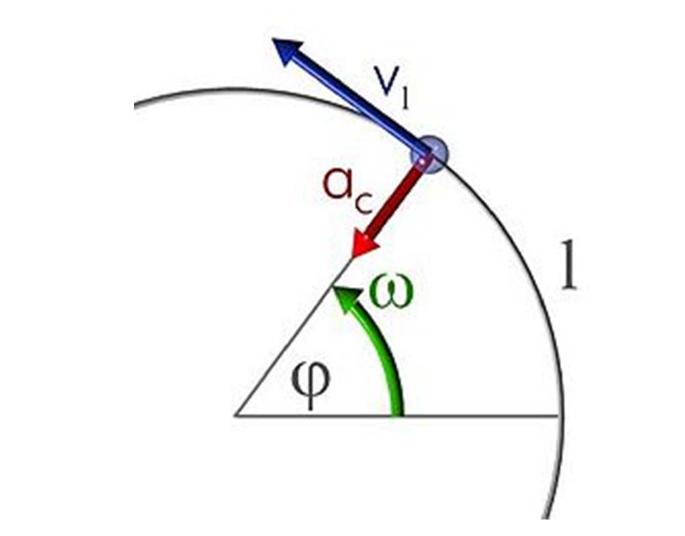
Pohyb v kruhu, stejně jako v přímce, může být stejný nebo nastane při akceleraci. V prvním případě je tento vzorec:

θ = ω * t

To znamená, že centrální úhel θ, na němž se těleso otáčí v čase t, je přímo úměrné úhlové rychlosti ω. Úhel θ je vyjádřen v radiánech a rychlost ω je vyjádřena v radiánech za sekundu.

Pokud v systému působí konstantní vnější síla síly, pohyb v kruhu nastane s určitým konstantním zrychlením α. V tomto případě bude pravdivý následující kinematický výraz:

θ = α * t 2/2

Pokud se systém nejprve otáčí určitou rychlostí ω ₀ a potom začne zvyšovat frekvenci otáčení při zrychlení α, pak se počínaje okamžikem času t, kdy se zrychlení objevilo, bude vzorec platný:

θ = ω ₀ * t + α * t 2/2

Všimněte si, že tento výraz je lineární kombinací dvou předchozích.

Vztah lineárních a úhlových kinematických charakteristik

Nahoře byl daný vzorec pro centripetální zrychlení, zapsaný lineární rychlostí v. Tento vzorec však může být také napsán z hlediska odpovídající úhlové charakteristiky ω.

Předpokládejme, že otáčející se těleso provedlo jednu otáčku kolem kruhu v čase t. Pak pro lineární a úhlovou rychlosti můžeme psát:

v = 2 * pi * r / t;

ω = 2 * pi / t

Od této doby je vidět, že modul lineární rychlosti v je r násobek velikosti magnitudy ω, to znamená:

v = ω * r

Tato rovnost spojuje úhlovou a lineární rychlost. Pomocí toho můžete napsat vzorec pro _c přes ω:

a _c = ω ² * r

Nyní vypočteme ve vzorci s rychlostí derivační čas pro levou a pravou stranu rovnosti, dostaneme:

dv / dt = dω / dt * r =>

a = α * r

Tato rovnost spojuje lineární zrychlení směřující tangenciálně k kružnici a jejímu úhlovému analogu α.

Je snadné dokázat, že centrální úhel natočení θ při pohybu kolem kružnice je spojen s délkou jeho oblouku L, a to následujícím výrazem:

L = θ * r

Zde, jestliže θ je rovno 2 * pi radians (plná revoluce), dostaneme délku kruhu L.

Řešení problému určení centrielní síly

Je známo, že kamenný kámen o hmotnosti 0,5 kg byl vázán na 1m dlouhé lano a začali ho otáčet s úhlovou četností 3 otáčky za sekundu. Je nutné nalézt napínací sílu lana Fc.

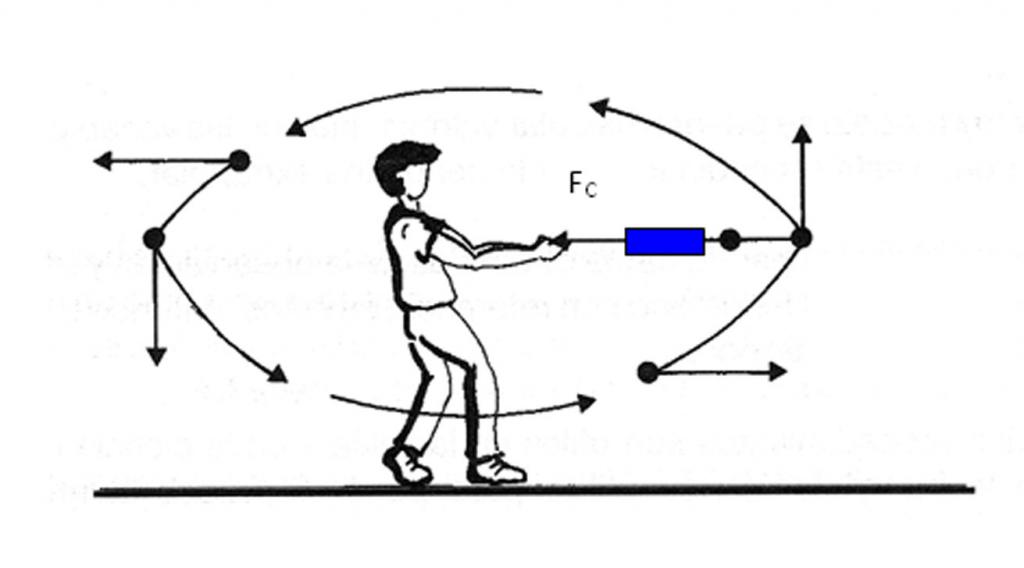
Napínací síla Fc je centriletní. Lze jej vypočítat podle vzorce:

Fc = m * a _c

Hmota kamene m je známá. Zcentrální zrychlení a _c lze vypočítat ze znalosti úhlové rychlosti ω. S frekvencí f nastavenou v úloze je množství ω souvislé výrazem:

ω = 2 * pi * f

Potom se centrielní zrychlení vypočte jako:

a _c = 4 * pi ² * f ² * r

Požadovaná síla F _c bude rovna:

Fc = 4 * pi ² * f ² * r * m

Je-li podmínkou problému nahrazení dat v tomto vzorci, dostaneme hodnotu síly Fc, přibližně rovnou 177,5 N.