Najít kořen rovnice? To je snadné!

V matematice existuje řada rovnic. Musí být vždy vyřešeny, to znamená hledat všechna čísla, která z ní činí skutečnou rovnost. Způsoby hledání řešení jsou určeny původní formou rovnice. Z toho bude záviset na počtu skutečných hodnot proměnné, které jsou označeny jako kořen rovnice. Toto číslo se může lišit od nuly do nekonečna.

Co znamená rovnice a její kořen?

Z názvu je zřejmé, že se rovná dvěma hodnotám, která mohou být reprezentována číselnými nebo abecedními výrazy. Navíc obsahují ještě neznámá množství. Nejjednodušší rovnice má pouze jednu.

Existuje velké množství typů rovnic, ale pojem kořen je pro ně vždy stejný. Kořen rovnice je taková hodnota neznámého čísla, při níž rovnice předpokládá skutečnou rovnost. Existují situace, kdy existuje několik takových čísel, pak se neznámé nazývá proměnná.

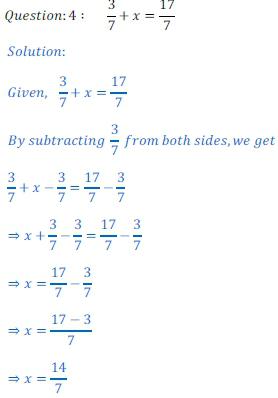
Hledání všech možných kořenů rovnice je jeho řešením. To znamená, že musíte provést řadu matematických operací, které zjednoduší. A pak vedou k rovnosti, která obsahuje pouze neznámé a číslo.

V algebře, při řešení rovnic, může dojít k situaci, že nebudou vůbec žádné kořeny. Pak říkají, že je nerozpustný. A v odpovědi na takovou rovnici je třeba si uvědomit, že neexistují žádná řešení.

Ale někdy se to opakuje. To znamená, že cizí kořeny se objevují v procesu mnoha transformací. Neposkytnou pravou rovnost při nahrazení. Čísla by proto měla být vždy kontrolována, aby se zabránilo situaci, kdy zbytečné kořeny v odpovědi. V opačném případě nebude rovnice považována za vyřešenou.

O lineární rovnici

Vždy se může přeměnit na záznam následujícího tvaru: a * x + v = 0. V něm je "a" vždy nenulová. Abychom pochopili, kolik kořenů má rovnice, bude třeba ji řešit v obecné podobě.

Transformace algoritmu:

• přesunout pojem "in" na pravou stranu rovnosti a nahradit jeho znamení opačným;
• rozdělí obě strany výsledné rovnosti na koeficient "a".

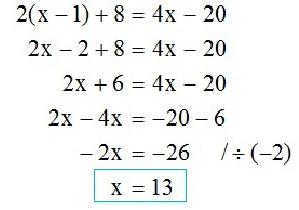
Obecný pohled na řešení je:

x = -in / a .

Z toho je jasné, že odpověď je jedno číslo. To je jen jeden kořen.

Kvadratická rovnice

Jeho obecná forma: a * x ² + b * x + c = 0 . Zde jsou koeficienty libovolné čísla kromě prvního, "a", který nemůže být rovný nule. Koneckonců se automaticky stává lineární. Odpověď na otázku, kolik kořenů má rovnice, již není tak přímočará jako v předchozím případě.

Všechno bude záviset na hodnotě diskriminující osoby. Vypočítá se podle vzorce D = ve ² - 4 a * s . Po výpočtech může být hodnota "D" větší, menší nebo rovna nule. V prvním případě budou kořeny rovnice dvě, ve druhé bude odpověď "bez kořenů" a třetí situace dá pouze jednu neznámou hodnotu.

Vzorce, které se používají k nalezení kořenů kvadratické rovnice a obsahují diskriminaci

Ve všeobecném případě, pokud je "D" kladné číslo, které se rovná nule, je třeba použít následující vzorec:

x _1,2 = (-в ± √Д) / (2 * a) .

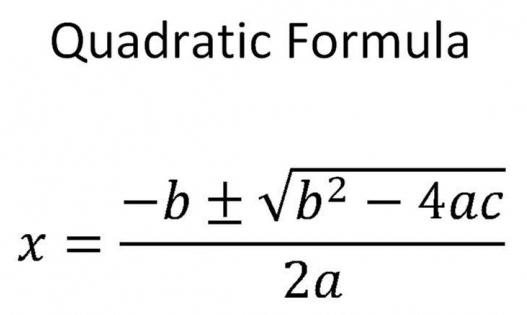
Tam jsou vždy dvě odpovědi. To je způsobeno skutečností, že původní vzorec je znaménkem plus / minus. Významně mění hodnotu neznámého.

Když se "D" rovná nule, kořen rovnice je jediným číslem. Jen proto, že druhá odmocnina od nuly je nula. Takže přidání a odečtení bude muset být nulové. Z tohoto čísla se nezmění. Proto může být vzorec kořenové rovnice napsán bez uvedení "D":

x = (-v) / (2 * a).

Pokud je diskriminátor záporný, není možné extrahovat druhou odmocninu od něj. Proto kořeny takové rovnice nebudou.

Poznámka To platí pro kurz, který není vyučen. komplexních čísel. Když jsou zadány, ukáže se, že v této situaci budou dvě odpovědi.

Vzorce pro výpočet kořenů kvadratické rovnice, která nepoužívají diskriminační

Mluvíme o větě Vietnamu. Platí v případě, kdy je kvadratická rovnice zapsána v mírně odlišné podobě:

x ² + c * x + c = 0.

Pak kořenový vzorec kvadratická rovnice se naplňuje řešení dvou lineárních:

x ₁ + x ₂ = -in
a
x ₁ * x ₂ = s.

Řeší se tím, že výraz pro jeden z kořenů je odvozen od prvního. A tato hodnota musí být nahrazena druhou. Takže druhý kořen se najde a pak první.

Tato možnost může vždy pocházet z obecné podoby kvadratické rovnice.

Stačí rozdělit všechny koeficienty na "a".

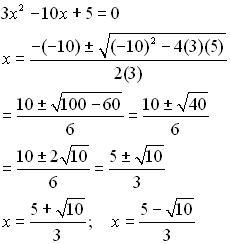
Co když potřebujete znát nejmenší hodnotu kořene?

Vyřešte rovnici a najděte všechna možná čísla, která jsou vhodná pro odpověď. A pak vyberte nejmenší. Bude to nejmenší kořen rovnice.

Nejčastěji se takové otázky vyskytují v úlohách, které mají stupeň vyšší než 2, nebo obsahují trigonometrické funkce. Příklad, kdy potřebujete najít nejmenší kořen, je následující rovnost:

2 x ⁵ + 2 x ⁴ - 3 x ³ - 3 x ² + x + 1 = 0.

Chcete-li najít každou hodnotu, kterou lze nazvat "kořen rovnice", je třeba tuto rovnici transformovat. První akce: seskupit členy v párech: první s druhým a tak dále. Pak z každého páru vytvořit společný faktor.

V každé konzole zůstane (x + 1). Společný faktor v prvním páru bude 2 x ⁴ , ve druhém 3 x ² . Nyní znovu musíte učinit zavedení společného faktoru, který bude stejný.

Po násobení (x + 1) bude (2 x ⁴ - 3 x ² + 1). Produkt dvou faktorů se rovná nule, pouze pokud jedna z nich má hodnotu rovnou nule.

První prvek je nula pro x = -1. To bude jeden z kořenů rovnice.

Jiné budou získány z rovnice tvořené druhou konzolou, která se rovná nule. Je to bivadratické. Chcete-li je vyřešit, musíte zadat notaci: x ² = y. Pak se rovnice výrazně změní a přijme obvyklou formu kvadratické rovnice.

Jeho diskriminant je D = 1. Je větší než nula, což znamená, že tam budou dva kořeny. První kořen se rovná 1, druhý je 0,5. Ale toto jsou hodnoty pro y.

Je třeba vrátit se k zadanému označení. x _1,2 = ± 1, x _3,4 = ± √0,5. Všechny kořeny rovnice: -1; 1; -0,5; √0.5. Nejmenší z nich je -1. To je odpověď.

Jako závěr

Připomenutí: všechny rovnice je třeba zkontrolovat na tom, zda je kořen vhodný. Možná je cizinec? Stojí za to zkontrolovat navrhovaný příklad.

Pokud nahradíme jednotku původně danou rovnicí místo "x", pak se ukáže, že 0 = 0. Tento kořen je správný.

Pokud x = -1, výsledek je stejný. Kořen je také vhodný.

Podobně, s hodnotami "x" rovnajícími se -0,5 a √0,5, vychází pravá rovnost. Všechny kořeny se hodí.

Tento příklad neposkytuje cizí kořeny. Není tomu tak vždy. Mohlo by být, že nejmenší hodnota by nebyla vhodná pro testování. Pak bych si musel vybrat ze zbytku.

Závěr: je nutné si vzpomenout na kontrolu a pečlivě přistupovat k řešení.