Volné vibrace. Obecné informace

V tomto článku budeme hovořit o volných oscilacích. Zvažte jejich příklady: matematické a pružinové kyvadlo, stejně jako oscilační obvod.

Mechanické vibrace

Oscilační pohyb nebo mechanické oscilace se nazývá pohyb těles nebo změna stavu, který se opakuje s časem. Příklady v mechaniky mohou být oscilace kyvadlů, strun, vyvažovačů hodin, membránových reproduktorů, mostů a dalších konstrukcí.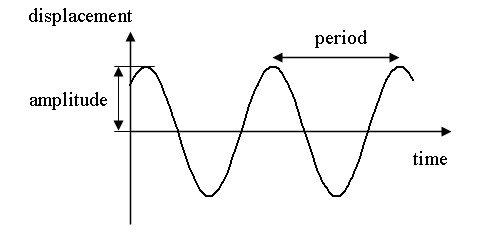

Oscilační pohyb se nazývá periodický, pokud se hodnoty fyzických veličin, které se mění během kmitů, opakují ve stejných časových intervalech.

Minimální interval (interval) času, po kterém se pozice těla opakuje během oscilačního pohybu, se nazývá perioda kmitání T. Počet kmitů, které tělo provádí za jednotku času, se nazývá kmitočet oscilace ν .

Harmonické

Mezi různými oscilačními pohyby jsou důležité harmonické oscilační pohyby.

Harmonic se nazývá oscilace, během níž materiální bod odchýlí se od rovnovážné polohy podle zákona sinus nebo kosinus.

Důležitost tohoto pohybu spočívá ve skutečnosti, že mnoho oscilujících pohybů v přírodě se blíží harmonické a také proto, že složité vibrace mohou být rozloženy do harmonických. Napíšeme posun materiálového bodu během harmonického pohybu:

x = Asin (ωt + φ ₀ )

Písmeno " x" označuje odchylku bodu, který osciluje od rovnovážné polohy. Maximální posunutí z rovnovážné polohy se nazývá amplituda. V našem případě x _max = A. Argument (ωt + φ ₀ ) se nazývá fáze oscilace a hodnota φ ₀ - počáteční fáze oscilace. Fáze umožňuje stanovit bodový posun v určitém časovém okamžiku.

Doba harmonické oscilace T , vzhledem k tomu, že doba oscilace fáze se změní na 2π , lze jej vypočítat podle vzorce:

T = 2π / ω.

Frekvence volných kmitů je:

v = 1 / T = ω / 2π.

Rychlost bodu s harmonickými kmity se nachází jako první derivace časového posunu:

v = dx / dt = Aokos (ωt + φ ₀ ).

Zrychlení bodu s harmonickými kmity se nalézá jako druhá derivace časového posunu:

a = dv / dt = Aω ² cos (ωt + φ ₀ ).

Zdarma

Pokud je tělo v oscilačním systému vyvedeno z rovnováhy a uvolněno, pak bude provádět tzv. Volné oscilace, které jsou vždy tlumeny.

Pro studium kmitů různé povahy často používají zařízení, nazývaná osciloskopy. Osciloskop (z latiny Oscillo - "váhat" a řečtina. Graf - "psát") - zařízení pro pozorování kmitů a jejich záznam v grafické podobě.

Amplituda oscilací v reálných systémech se s časem snižuje a oscilace nakonec přestávají, takže volná oscilace jsou vždy tlumeny.

Doba oscilací nezávisí na jejich amplitudě, protože v reálných mechanických systémech dochází vždy ke ztrátě mechanické energie.

Vyšetřování volných oscilací v systému "zatížení-pružina", bez ztráty mechanická energie lze konstatovat, že doba takových kmitů je určena podle vzorce:

T = 2π / ω,

kde ω je cyklická frekvence.

Frekvence volných kmitů se měří podle vzorce:

v = 1 / T = ω / 2π.

Matematické kyvadlo

Matematické kyvadlo je považováno za bodové tělo zavěšené z nevýbušného a beztížného závitu. Matematické kyvadlo je abstraktní koncept, protože za prvé v přírodě neexistují žádné bodové těla a za druhé neexistují žádné naprosto nevyrovnatelné a beztížné závity. Nicméně s určitým přiblížením může být matematické kyvadlo považováno za kuličku zavěšenou z nití. Když je míč ve stavu rovnováhy, působí ji gravitační síla a síla pružnosti nitě, které se navzájem vyvažují, jinými slovy, výsledkem těchto sil je nula.

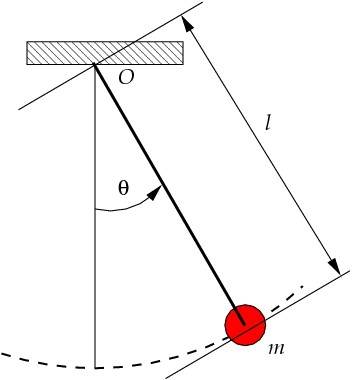
Perioda oscilace matematického kyvadla může být vypočtena podle vzorce:

T = 2π / ω,

kde cyklická frekvence volných kmitů ω2 = l / g a l je délka závitu.

Podle vzorce lze konstatovat, že doba oscilace matematického kyvadla nezávisí na tělesné hmotnosti, ale je určena pouze délkou zavěšení a zrychlením volného pádu.

Jarní kyvadlo

Dalším příkladem harmonických volných kmitů jsou oscilace těla na pružině. Ve stavu rovnováhy není pružina deformována, elastická síla neovlivňuje tělo. Třecí síla mezi tělem a nosičem je také nulová. Síla přitažlivosti je vyvážena sílou reakce podpěry. Pokud je tělo vyvedeno z rovnováhy, pohybuje se podél osy OX ve vzdálenosti x = ± A a poté uvolní, kyvadlo volně osciluje pod působením elastické síly a volné oscilace kyvadla se stanou jako x = Asinwt.

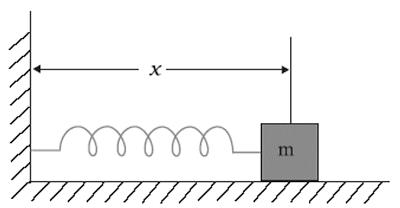
Doba volných kmitů kyvadla na pružině se rovná:

T = 2π / ω,

kde frekvence cyklické oscilace ω2 = k / m, k je tuhost pružiny, m je tělesná hmotnost.

Jak je zřejmé z vzorce, doba a frekvence oscilací pružinového kyvadla nezávisí na tom gravitační zrychlení a jsou určeny pouze hmotností zavěšeného těla a pružinovou tuhostí.

Elektrické oscilace v obvodu

Elektrický obvod, ve kterém jsou možné volné elektromagnetické kmity, se nazývá oscilační obvod. Skládá se z kondenzátoru s kapacitou C, cívky s indukčností L a odporu s odporem R (v reálném technickém obvodu, odpor cívky a spojovacích vodičů hrají roli odporu).

Ohmův zákon pro uzavřený obvod, který neobsahuje externí zdroj proudu a ve kterém se vyskytují volné elektromagnetické oscilace, je napsán v této podobě:

JR + U = - L (dJ / dt),

kde U = q / C je napětí přes kondenzátor, q je náboj kondenzátoru, J = dq / dt je proud v obvodu.

Volné oscilace v obvodu jsou harmonické, proto se mění podle následujícího zákona:

q (t) = q ₀ cos (ωt + φ ₀ ).