Jak vypočítat metry čtverečních a jaká je plocha místnosti

Možná, každý z nás má okamžik, kdy nastane další otázka: "Jak vypočítat čtvereční metry místnosti nebo místa?". Tento úkol lze snadno řešit pomocí věd o geometrii škol.

Kdy může vyžadovat měření plochy

V některých případech je nutné rychle zjistit, jak vypočítat metry čtverečních v určité oblasti. V podstatě je tento úkol nastaven pro lidi, kteří začali opravovat. Správný výpočet rozložení místnosti pomůže vypočítat množství potřebných stavebních materiálů. V podstatě je otázka, jak vypočítat čtvereční metry místnosti nebo celého domu, pokud se plánuje:

• výměna podlah;
• pokládka tepla nebo hydroizolace;
• demontáž nebo instalace parketových podlah;
• generální oprava;
• přestavba domova.

Měření plochy pravoúhlých místností

Tato klasická úloha zpravidla nezpůsobuje otázky jako "Jak správně vypočítat čtvereční metry?". Pravidlo, podle kterého je oblast obdélníku rovna výsledku jeho sousedních stran, je dobře známá ze školy. Proto pro výpočet plochy místnosti stačí vynásobit délky stěn, které mají společný úhel. Například prostor s délkou stran 3 m a 4 m bude mít plochu 12 m ² . V případě čtvercové místnosti nebude vůbec těžké měřit oblast - stačí násobit délku jedné ze stran čtvercové místnosti sama. Totéž bude odpovědí na otázku, jak vypočítat čtvereční metry zdi.

Plocha trojúhelníkových místností. V domcích starých nebo samostatných budov se nacházejí takové trojúhelníkové rohy. V případě připomenutí pokoje pravý trojúhelník otázka, jak vypočítat čtvereční metry, nevzniká. Všichni si pamatují, že oblast pravoúhlého trojúhelníku je polovičním produktem jeho nohou. 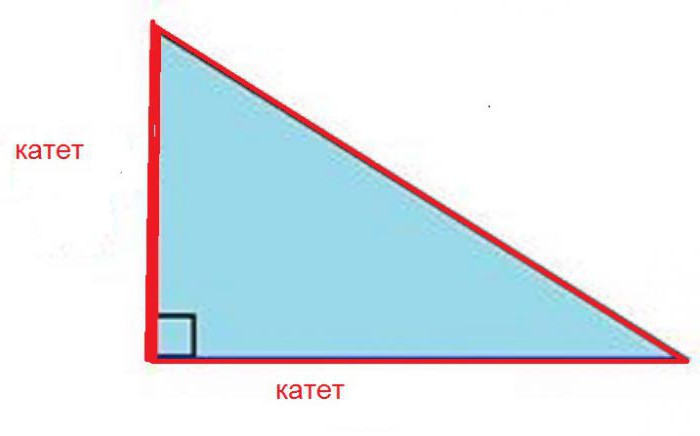Pokud je trojúhelník nestandardní, pomocí konstrukční úrovně snižujeme výšku z nejširšího úhlu na opačnou stranu. Výsledkem je získání dvou pravoúhlých trojúhelníků a výpočet jejich ploch.

Měření plochy nepravidelného polygonu

Komplikované rozvržení moderních budov nebo "zakřivení" stavitelů vedou k vzniku nestandardních rozvržení. Nejčastějším případem je místnost, která se podobá lichoběžníku. V případě takové katastrofy, geometrie přijde na záchranu znovu.

Dvě protilehlé strany lichoběžníku jsou rovnoběžné. Vyjdeme z rohů menší strany výšky a sbíhají se k většímu. Z hlediska výsledného čísla bude vypadat takto:

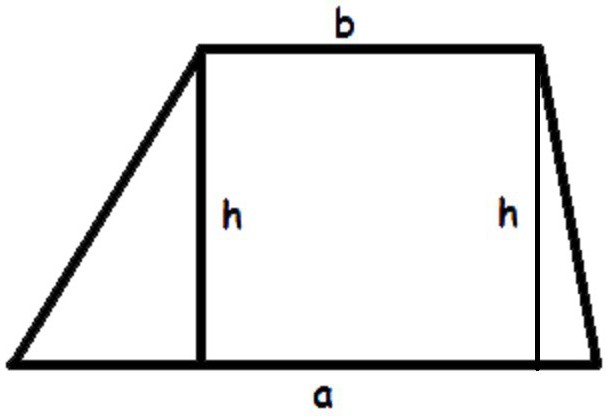
Z obrázku je zřejmé, že lichoběžník je ve skutečnosti obdélník s dvěma trojúhelníky na jeho stranách. Jak vypočítat metry čtverečních obdélník, který už víme. Můžeme také určit oblast dvou pravých trojúhelníků. Nakonec trapézní oblast bude sestávat ze součtu ploch obdélníku a dvou trojúhelníků.

Komplexní tvary

V nových apartmánech vedou lety architektonických myšlenek k vzhledu zaoblených ploch, kde konvexní nebo konkávní stěny popisují hladké křivky, a podlaha je zase projektem práce architekta a vlastního bolesti hlavy. Jak vypočítat povrch čtverečních metrů v tomto případě?

Znovu, zpět na kurz matematiky. Nejprve si připomínáme, že oblast kruhu lze vypočítat pomocí takového úžasného vzorce:

S = π R2

Takže je velmi snadné počítat kulaté plochy, stačí znát poloměr kruhu.

V obzvláště obtížných případech dokonce ani magické číslo Pi nepomůže. Pro výpočet oblastí složitých tvarů se bude muset uchýlit k integrálám.

Vyděšený? Nestojí to za to. Integrály v matematice se nazývají součtem sady malých částic. Nestačí vám nic, aby se měřený povrch zlomil na úzké pásy, což jsou zjednodušené obdélníky. V případě malé šířky takového obdélníku může být zakřivení na jeho základně zanedbatelné. Výsledný tvar bude vypadat takto: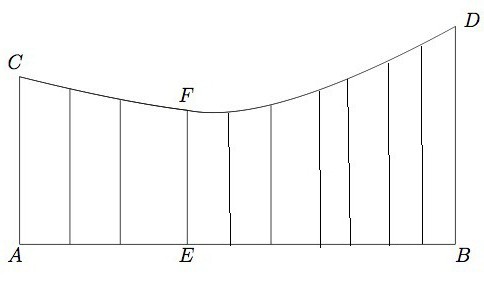

Vypočítáme plochy každého obdélníku, sumarizujeme jejich hodnoty a plocha komplexního povrchu se vypočítá bez zbytečných potíží.

Jak měřit

V ideálním případě byste měli byt od nábytku uvolnit a běžet po něm. Jelikož je to možné pouze v případě přechodu na nové bydliště, jednáme se jinak. Za prvé, můžete měřit prostor místnosti přes strop, v naději z celého srdce rovnoběžnost rovin strop a podlaha. Plochu stropu lze stanovit pomocí výše popsaných metod.

Druhou metodou je určit obvod místnosti měřením délky jejích stěn ve stejné výšce. Chcete-li to provést, můžete použít nanášecí barvu a táhnout ji podél stěn ve stejné výšce.

Jak vidíte, kurz geometrie školy není tak zbytečný, jak jsme si mysleli předtím. Získané znalosti se ukázaly být docela praktické a pomohly nám spočítat náměstí našeho domova.