Jak vypočítat objem různých geometrických těles?
V průběhu stereometrie je jednou z hlavních otázek, jak vypočítat objem určitého geometrického tělesa. Všechno začíná jednoduchým rovnoběžkem a končí kuličkou.
V životě se také často musí vypořádat s podobnými problémy. Například k výpočtu objemu vody, která je umístěna v kbelíku nebo barelu.
Vlastnosti odpovídají objemu každého těla
- Tato hodnota je vždy kladné číslo.
- Pokud může být tělo rozděleno na části tak, aby nebyly žádné průsečíky, pak se celkový objem rovná součtu objemů dílů.
- Rovné tělesa mají stejný objem.
- Pokud menší těleso zapadne do většího, pak je objem prvního menšího než druhý.
Obecná notace pro všechny těla
V každém z nich jsou okraje a základny, ve kterých jsou postaveny výšky. Tyto prvky jsou proto pro ně stejně výrazné. Takto jsou napsány ve vzorcích. Jak vypočítat objem každého těla - dozvíme se více a uplatníme nové dovednosti v praxi.
| Označení | Vysvětlení |
| a | okraj těla, kde jsou všechny stejné |
| V | objemu |
| S 0 | základní plochu |
| h | výšku |
| r | poloměr |
Některé vzorce mají jiné hodnoty. Jejich jmenování bude projednáno, pokud taková potřeba vznikne.
Prism, rovnoběžnost (rovná a šikmá) a krychle
Tato těla jsou kombinována, protože vypadají velmi podobně a vzorce pro výpočet objemu jsou totožné:
V = S 0 * h.
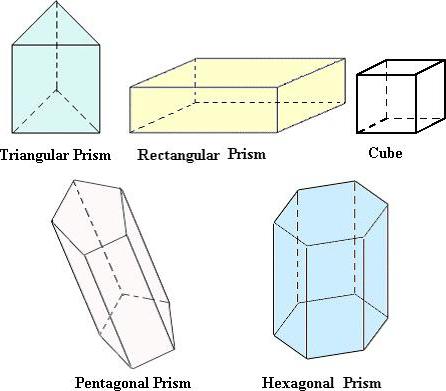
Pouze S 0 se liší. V případě rovnoběžnosti se vypočte jako u obdélníku nebo čtverce. V hranolu může být základem trojúhelník, rovnoběžník, libovolný čtyřúhelník nebo jiný mnohoúhelník.
Pro kostku je vzorec výrazně zjednodušený, protože všechny jeho rozměry jsou stejné:
V = a 3 .
Pyramid, tetraedrón, zkrácená pyramida
Pro první z těchto těles existuje takový vzorec pro výpočet objemu:
V = 1/3 * S 0 * n.
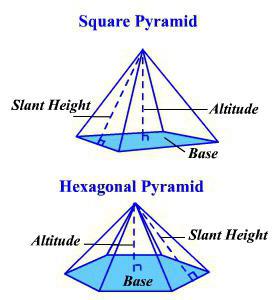
Tetrahedron je zvláštní případ trojúhelníkové pyramidy. Všechny okraje v něm jsou stejné. Proto opět získáme zjednodušený vzorec:
V = (a 3 * √2) / 12 nebo V = 1/3 S 0 h
Zkrácená pyramida se stává, když je její horní část odříznuta. Proto je jeho objem rovný rozdílu mezi dvěma pyramidy: ten, který by byl neporušený a vzdálený vrchol. Pokud je možné zjistit obě základy takové pyramidy (S1 je větší a S2 je menší), pak je vhodné použít tento vzorec pro výpočet objemu:
V = 1/3 * h * (S 1 + √ (S 1 S 2 ) + S 2 ).
Válec, kužel a zkrácený kužel
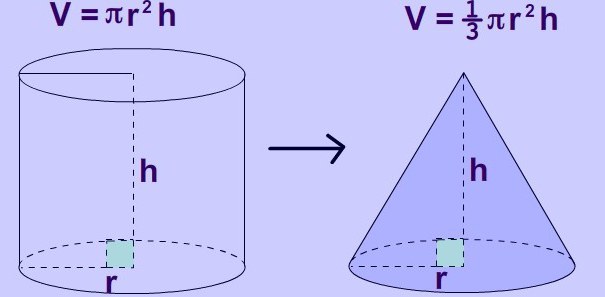
Pokud chcete vypočítat objemu válce Můžete použít vzorec, který je určen pro hranol. Někdy je vhodné napsat to v této podobě:
V = π * r 2 * h.
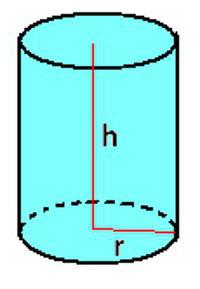
Situace s kuželem je poněkud komplikovanější. Pro něj existuje vzorec:
V = 1/3 π * r 2 * h. Je velmi podobný tomu, který je určen pro válec, pouze hodnota se třikrát sníží.
Stejně jako se zkrácenou pyramidou není situace snadná s kuželem, který má dvě základny. Vzorec pro výpočet objemu zkráceného kužele je následující:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2 ). Zde r1 je poloměr dolní základny, r2 je horní (menší).
Míč, míčové segmenty a sektor
Jedná se o nejobtížněji zapamatovatelné vzorce. Pro objem míče vypadá takto:
V = 4/3 π * r 3 .
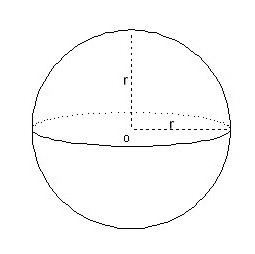
V problémech se často vyskytuje otázka, jak vypočítat objem sférického segmentu - část koule, která je řezána paralelně s průměrem. V takovém případě přijde na záchranu následující vzorec:
V = π h 2 * (r - h / 3). V tom je pro h určena výška segmentu, tj. Část, která jde podél poloměru míče.
Sektor je rozdělen na dvě části: kužel a segment koulí. Proto je jeho objem definován jako součet těchto těles. Vzorec po transformaci vypadá takto:
V = 2/3 πr 2 * h. Zde h je také výška segmentu.
Příklady úkolů
Pro válce, kuličky a kuželky
Stav: průměr válce (1 těleso) se rovná jeho výšce, průměru koule (2 tělo) a výšce kužele (3 tělo); zkontrolujte proporcionalitu objemů V 1 : V 2 : V 3 = 3: 2: 1
Rozhodnutí. Nejprve je třeba napsat tři vzorce pro svazky. Pak zvažte, že poloměr je o polovinu průměru. To znamená, že výška bude rovna dvěma poloměrům: h = 2r. Po provedení jednoduché náhrady se ukázalo, že vzorce pro svazky budou vypadat takto:
V 1 = 2 π r 3 ; V 3 = 2/3 π r 3 . Vzorec pro objem míče se nemění, protože se v něm nezobrazuje výška.
Nyní zůstane zapsat objemové vztahy a snížit hodnotu 2π a r3. Ukázalo se, že V 1 : V 2 : V 3 = 1: 2/3: 1/3. Tato čísla snadno vedou k záznamu 3: 2: 1.
Odpověď zní. V 1 : V 2 : V 3 = 3: 2: 1.
O objemu míče
Stav: dva vodní melouny s poloměrem 15 a 20 cm; Jaký je nejvýhodnější způsob, jak jíst: první čtyři nebo druhá druhá?
Rozhodnutí. Chcete-li odpovědět na tuto otázku, musíte najít poměr objemů kusů, které se dostanou od každého melounu. Vzhledem k tomu, že jsou kuličky, je třeba napsat dva vzorce pro svazky. Pak vezměte v úvahu, že od prvního dostanou jen čtvrtou část a od druhé - osmou.
Zbývá zaznamenat poměr objemů dílů. Bude to vypadat takto:
(V 1 : 4) / (V 2 : 8) = (1/3 π r 1 3 ) / (1/6 π r 2 3 ). Po konverzi zůstává pouze frakce: (2 r 1 3 ) / r 2 3 . Po nahrazení hodnot a výpočtů se získá frakce 6750/8000. Z toho je zřejmé, že část z prvního melounu bude menší než od druhé.
Odpověď zní. Je výhodnější jíst osmou část melounu o poloměru 20 cm.
O objemu pyramidy a krychle
Stav: je jílová pyramida s obdélníkovou základnou 8x9 cm a výškou 9 cm; vyrobili kousek ze stejné hlíny; jaký je jeho okraj?
Rozhodnutí. Pokud označujeme strany obdélníku písmeny v písmenu, pak je oblast základny pyramidy vypočítána jako jejich produkt. Pak vzorec pro jeho objem:
V 1 = 1/3 * slunce * h.
Vzorec pro objem krychle je uveden v článku výše. Tyto dvě hodnoty jsou stejné: V 1 = V 2 . Zbývá srovnávat pravé strany vzorců a provést potřebné výpočty. Ukázalo se, že okraj krychle se bude rovnat 6 cm.
Odpověď zní. a = 6 cm
O objemu rovnoběžnosti
Stav: je nutné vyrobit krabici s kapacitou 0,96 m 3 , její šířka a délka jsou známy - 1,2 a 0,8 m; Jaká by měla být její výška?
Rozhodnutí. Vzhledem k tomu, že základna rovnoběžnosti je obdélník, její oblast je definována jako produkt délky (a) a šířky (c). Proto vzorec pro svazek vypadá takto:
V = a * c * n.
Z ní lze snadno určit výšku rozdělení objemu na plochu. Ukazuje se, že výška by měla být rovna 1 m.
Odpověď zní. Výška krabice je jeden metr.