Kinetická energie - energie pohybu těles
Potenciální a kinetická energie nám umožňují charakterizovat stav každého těla. Je-li prvně použit v systémech interaktivních objektů, pak je druhý spojen s jejich pohybem. Tyto typy energie jsou zpravidla zvažovány, když síla spojující těla je nezávislá na trajektorii pohybu. V takovém případě jsou důležité pouze počáteční a konečné pozice.
Obecné informace a koncepce
Kinetická energie systému je jednou z nejdůležitějších vlastností. Fyzici rozlišují dva typy takové energie v závislosti na typu pohybu:
• progresivní;
• otáčení.
Kinetická energie (E k ) je rozdíl mezi celkovou energií systému a zbytkovou energií. Na základě toho můžeme říci, že je to způsobeno pohybem systému. Tělo to má jen tehdy, když se pohybuje. V klidu je objekt nulový. Kinetická energie všech těles závisí pouze na rychlosti pohybu a jejich hmotách. Celková energie systému je přímo závislá na rychlosti jeho objektů a vzdálenosti mezi nimi.
Základní vzorce
V případě, že jakákoli síla (F) působí na tělo, které je v klidu tak, aby se dostalo do pohybu, můžeme mluvit o tom, že děláme práci dA. Hodnota této energie dE bude vyšší, čím více práce bude provedeno. V tomto případě platí následující rovnost: dA = dE.
Vzhledem k dráze, kterou tělo cestovalo (dR) a jeho rychlosti (dU), můžete použít zákon 2 Newtona, podle kterého: F = (dU / dE) * m.
Výše uvedený zákon je používán pouze tehdy, když existuje inerciální referenční systém. Existuje další důležitá nuance, která je při výpočtech brána v úvahu. Hodnota energie je ovlivněna volbou systému. Takže podle systému SI se měří v joulech (J). Kinetická energie těla se vyznačuje hmotností m, stejně jako rychlostí pohybu υ. V tomto případě bude: E k = ((υ * υ) * m) / 2.
Na základě výše uvedeného vzorce lze konstatovat, že kinetická energie je určována hmotností a rychlostí. Jinými slovy je to funkce těla.
Energie v mechanickém systému
 Kinetická energie je mechanická energie systému. Záleží na rychlosti jeho bodů. Skutečná energie materiální bod je reprezentován následujícím vzorcem: E = 1 / 2m² 2, kde m je hmotnost bodu a υ je jeho rychlost.
Kinetická energie je mechanická energie systému. Záleží na rychlosti jeho bodů. Skutečná energie materiální bod je reprezentován následujícím vzorcem: E = 1 / 2m² 2, kde m je hmotnost bodu a υ je jeho rychlost.
Kinetická energie mechanického systému je aritmetickým součtem stejných energií všech jeho bodů. Rovněž může být vyjádřena následujícím vzorcem: E k = 1 / 2My c2 + Ec, kde υc je rychlost středu hmotnosti, M je hmotnost systému, Ec je kinetická energie systému při pohybu kolem středu hmoty.
Pevná energie
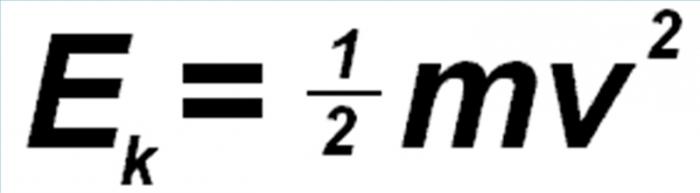 Kinetická energie těla, která se postupně pohybuje, je určena stejnou energií bodu s hmotností rovnou hmotnosti celého těla. Pro výpočet ukazatelů při pohybu použijte složitější vzorce. Změna této energie systému v okamžiku jeho pohybu z jedné polohy do druhé nastává pod vlivem aplikovaných vnitřních a vnějších sil. To se rovná součtu práce Aue a A'u těchto sil během tohoto pohybu: E2 - E1 = Σu Aue + Σu A'u.
Kinetická energie těla, která se postupně pohybuje, je určena stejnou energií bodu s hmotností rovnou hmotnosti celého těla. Pro výpočet ukazatelů při pohybu použijte složitější vzorce. Změna této energie systému v okamžiku jeho pohybu z jedné polohy do druhé nastává pod vlivem aplikovaných vnitřních a vnějších sil. To se rovná součtu práce Aue a A'u těchto sil během tohoto pohybu: E2 - E1 = Σu Aue + Σu A'u.
Tato rovnost odráží větu o změně kinetické energie. S jeho pomocí jsou řešeny nejrůznější problémy mechaniky. Bez tohoto vzorce není možné vyřešit řadu důležitých úkolů.
Kinetická energie při vysokých rychlostech
Pokud je rychlost těla blízká rychlosti světla, lze kinetickou energii bodu materiálu vypočítat podle následujícího vzorce:
E = m0c2 / ı1-υ2 / c2 - m0c2,
kde c je rychlost osvětlení ve vakuu, m0 je hmotnost bodu, m0c2 je energie bodu. Při nízké rychlosti (υ Během otáčení tělesa kolem osy je každý z jeho elementárních objemových objemů (mi) popsán jako kruh s poloměrem ri. V tomto okamžiku má objem lineární rychlost υi. Vzhledem k tomu, úhlová rychlost otáčky všech objemů budou stejné: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). Kinetická energie rotace pevné látky je součtem všech stejných energií jejích elementárních objemů: E = m1y1 2/2 + miύi 2/2 + ... + mnύn 2/2 (2). Při použití výrazu (1) získáme vzorec: E = Jz ω 2/2, kde Jz je moment setrvačnosti těla kolem osy Z. Když porovnáváme všechny vzorce, je zřejmé, že moment setrvačnosti je měřítkem setrvačnosti těla během rotační pohyb. Vzorec (2) je vhodný pro objekty, které se otáčejí kolem pevné osy. Kinetická energie těla, pohybujícího se po rovině, se skládá z energie rotace a translačního pohybu: E = mύc2 / 2 + Jz ω 2/2, kde m je hmotnost pohybujícího se těla, Jz je moment setrvačnosti těla kolem osy, υc je rychlost středu hmoty, ω je úhlová rychlost. Změna hodnoty kinetické energie úzce souvisí s potenciálem. Podstatu tohoto jevu lze pochopit prostřednictvím zákona o zachování energie v systému. Součet E + dP během pohybu těla bude vždy stejný. Změna hodnoty E vždy nastává současně se změnou v dP. Takto jsou přeměňovány, jako by do sebe proudily. Takový jev lze nalézt téměř ve všech mechanických systémech. Pro výpočet energetické hodnoty se zvolí libovolný moment (považuje se za počáteční) a referenční systém. Je možné určit přesné množství potenciální energie pouze v zóně vlivu sil, které nezávisí na trajektorii těla při práci. Ve fyzice se tyto síly nazývají konzervativní. Mají neustálou souvislost se zákonem o zachování energie. Pokud je vnější vliv minimální nebo snížen na nulu, bude studovaný systém vždy v takovém stavu, ve kterém bude mít potenciální energie také tendenci k nule. Například míč, který bude vyhozen, dosáhne hranice této energie v horní části trajektorie pohybu a ve stejném okamžiku začne klesat. V tuto chvíli se nahromaděná energie za letu mění na pohyb (vykonává se práce). Pro potenciální energii je v každém případě interakce alespoň dvou těles (v příkladu s kuličkou to ovlivňuje gravitace planety). Kinetická energie může být vypočtena jednotlivě pro jakékoliv pohyblivé tělo. Potenciální a kinetická energie se mění výhradně ve vzájemné interakci těl, když síla působící na tělo vykonává práci, jejíž hodnota se liší od nuly. V uzavřeném systému se práce síly síly nebo elasticity rovná změně potenciální energie objektů se znaménkem "-": A = - (Ep2 - Ep1). Práce síly nebo elasticity se rovná změně energie: A = Ek2 - Ek1. Ze srovnání obou rovnic je zřejmé, že změna v energii objektů v uzavřeném systému se rovná změně potenciální energie a je naopak v znaménku: Ek2 - Ek1 = - (Ep2 - Ep1) nebo jinak: Ek1 + Ep1 = Ek2 + Ep2. Z této rovnosti je zřejmé, že součet těchto dvou energií těl v uzavřeném mechanickém systému a vzájemně působící síly pružnosti a agrese zůstávají vždy konstantní. Na základě výše uvedeného lze učinit závěr, že při studiu mechanického systému je třeba vzít v úvahu interakci potenciálních a kinetických energií. 
Rotační energie systému
Planární pohyb těla

Změna energie v mechanickém systému
Energetické propojení
Potenciální a kinetická energie jsou úzce spjaty. Jejich suma může být reprezentována jako celková energie systému. Na molekulární úrovni to je vnitřní energie tělo. Je přítomen neustále, pokud existuje alespoň nějaká interakce mezi těly a tepelným pohybem. Volba referenčního systému
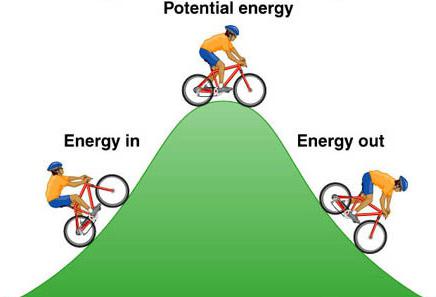
Podstata rozdílu mezi potenciální a kinetickou energií
Propojení různých energií