Otočný pohyb a úhlová rychlost pevného tělesa

V tomto článku budeme diskutovat o fyzikálních veličinách, které charakterizují rotační pohyb tělesa: úhlová rychlost, úhlový posun, úhlové zrychlení, točivý moment.

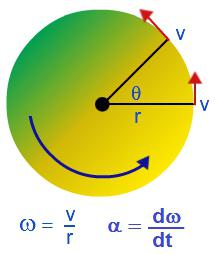
Pevné těleso je sbírka pevně spojených bodů materiálu. Když se pevné těleso otáčí kolem jakékoli osy, jednotlivé body, ze kterých se přidává, se pohybují po kružnicích různých poloměrů.

Například po určitou dobu, během které tělo dělá jednu otáčku, oddělují materiálové body, které tvoří pevné tělo, budou procházet různými cestami, takže oddělené body budou mít různé lineární rychlosti. Popište rotaci pevné látky pomocí lineárních rychlostí jednotlivce bodů - obtížné.

Úhlové posunutí

Při analýze pohybu jednotlivých bodů materiálu lze však zjistit, že ve stejném časovém úseku se všechny otáčejí kolem osy ve stejném úhlu. To znamená, že při popisu rotace pevné látky je vhodné použít takové fyzikální množství jako úhlový posun:

φ = φ (t).

Úhlová rychlost a úhlové zrychlení

Otočný pohyb lze charakterizovat úhlovou rychlostí: ω = Δφ / Δt.

Úhlová rychlost charakterizuje rychlost otáčení těla a je rovna poměru změn úhlu natočení s časem, ve kterém došlo. Měřeno v radiánech za sekundu: [ω] = rad / s.

Úhlová rychlost otáčení souvisí s lineární rychlostí následujícím vztahem: v = Rω, kde R je poloměr kruhu, ve kterém se tělo pohybuje.

Rotační pohyb těleso je charakterizováno jinou fyzikální veličinou - úhlovým zrychlením, které se rovná poměru změny úhlové rychlosti k době, během níž nastala: ε = Δω / Δt. Jednotka měření úhlového zrychlení: [ε] = rad / s ² .

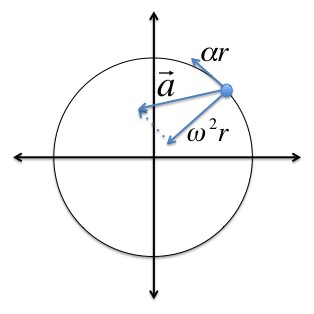
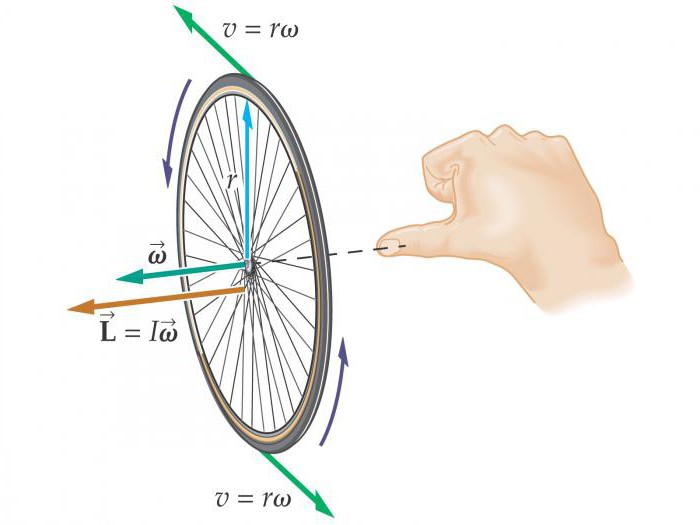
Úhlová rychlost a úhlové zrychlení jsou pseudovektory, jejichž směr závisí na směru otáčení. To může být určeno pravidlem správného šroubu.

Jednotný rotační pohyb

Jednotný rotační pohyb se provádí s konstantní úhlovou rychlostí a je popsán pomocí následujících rovnic: ε = 0, ω = konst, φ = φ ₀ + ωt, kde φ ₀ je počáteční hodnota úhlu natočení.

Rovnoměrně zrychlený rotační pohyb

Rovnoměrně zrychlený rotační pohyb probíhá s konstantním úhlovým zrychlením a je popsán pomocí následujících rovnic: ε = const, ω = ω ₀ + εt, φ = φ ₀ + ω ₀ t + εt 2/2.

Během otáčení pevné látky centrální zrychlení každý bod tohoto těla lze nalézt takto: ɑ _c = v ² / R = (ωR) ² / R = ω ² R.

Při rotaci pevné látky se urychluje tangenciální zrychlení jejích bodů podle vzorce: = Δv / Δt = Δ (ωR) / Δt = R (Δω / Δt) = Rε.

Moment síly

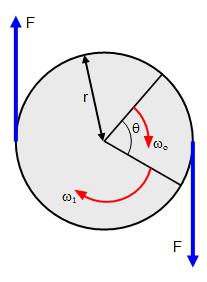
Pokud se vezmeme v úvahu fyzického problému, nejednáme se o hmotný bod, ale s pevným tělem, pak působení několika sil působících na něj v různých částech tohoto těla nemůže být omezeno na působení jediné síly. V tomto případě zvažte okamžik sil.

Moment síly se nazývá produkt síly na rameni. Toto je vektorová veličina a je zjištěna podle vzorce: M = RFsinα, kde α je úhel mezi vektory R a F. Jestliže na těle působí několik momentů síly, jejich činnost může být nahrazena jejich výsledným součtem těchto momentů: M = M ₁ + M ₂ + ... + M _n .

Experimenty a zkušenosti ukazují, že pod působením momentu síly se mění úhlová rychlost těla, to znamená, že tělo má úhlové zrychlení. Zjistíme, jak úhlové zrychlení materiálu bodu (soubor bodů materiálu) závisí na použitém točivém momentu: F = m, RF = Rma = R ² mβ, β = M / mR ² = M / I, kde I = mR ² je moment setrvačnosti materiálu bodů. Všimněte si, že moment setrvačnosti těla závisí jak na hmotnosti těla, tak na poloze této hmoty vzhledem k ose rotace.

Příklady řešení problémů

Úloha 1. Rotor centrifugy činí 2 • 10 ⁴ ot./min. Po vypnutí motoru se jeho rotace zastaví po 8 minutách. Zjistěte úhlové zrychlení a počet otáček rotoru od okamžiku vypnutí motoru, až se zastaví, s ohledem na to, že pohyb rotoru je rovnoměrně zrychlen.

Řešení

Najděme úhlové zrychlení s přihlédnutím k tomu, že úhlová rychlost s rovnoměrně zrychleným pohybem je popsána rovnicí: ω (t) = ω ₀ - εt.

Vzhledem k tomu, že na konci pohybu je rychlost nula, zjistíme: ε = ω ₀ / t = 2πn / t.

Přenos těchto úkolů na jednotku SI jednotek (n = 333 rev / s; t = 480 s) získáme: ε = 2π333 / 480 = 4,36 (rad / s ² ).

Úhel natočení centrifugačního rotoru v čase t bude: φ (t) = φ ₀ + ω ₀ t + εt 2/2. Čtení výrazu pro úhlové zrychlení a skutečnost, že φ ₀ = 0 , zjistíme: φ (t) = ω ₀ t / 2 = πnt.

Počet otáček rotoru během této doby bude: N = φ (t) / 2π = πnt / 2π = nt = 8 • 10 ⁴ (vol.).

Odpověď: úhlové zrychlení je 4,36 rad / s ² ; počet otáček rotoru od okamžiku vypnutí motoru až do úplného zastavení je 8 • 10 ⁴ ot./min.

Úkol 2. Disk o hmotnosti 1 kg a o poloměru 20 cm se otáčí při frekvenci 120 ot./min. za minutu. Pod působením brzdového zařízení na okraji disku se začalo jednat třecí síla 10 N. Najděte čas zastavit disk poté, co začal působit sílu tření.

Řešení

Najděte brzdný moment působící na disk: M = RF.

Najít úhlové zrychlení disku: ε = M / I = FR / mR ² = F / mR.

Najdeme čas, po který bude disk zastaven: t = ω ₀ / ε , kde ω ₀ je počáteční úhlová rychlost disku, která se rovná 2πv.

Provedeme výpočty: t = 2πv / ε = 2πvmR / F = 6,28 • 2 • 1 • 0,2 / 10 = 2,5 (s).

Odpověď: doba zastavení je 2,5 sekundy.