Znamení, podstatné prvky a vlastnosti rovnoramenného trojúhelníku

První historici naší civilizace - starověcí Řekové - zmiňují Egypt jako místo narození geometrie. Je obtížné nesouhlasit s nimi a vědět, s jakou ohromnou přesností byly postaveny obří hroby faraonů. Vzájemné uspořádání pyramidových rovin, jejich proporce, orientace podél kardinálních bodů - by bylo nemyslitelné dosáhnout takové dokonalosti bez znalosti základů geometrie.

Slovo "geometrie" může být přeloženo jako "rozměr Země". A slovo "země" se nejeví jako planeta - součást sluneční soustavy, ale jako rovina. Označení oblastí pro zemědělství je s největší pravděpodobností základem vědy geometrických tvarů, jejich typů a vlastností.

Trojúhelník je nejjednodušší prostorová postava planimetrie, která obsahuje pouze tři body - vrcholy (nemůže být méně). Základem základů může být, proč se v ní objevuje něco tajemného a starověkého. Celé vidění uvnitř trojúhelníku je jedním z nejstarších známých okultních znamení a geografie jeho distribuce a časového rámce jsou prostě úžasné. Ze starověkých egyptských, sumerských, aztéckých a dalších civilizací až po moderní komunity okultních milenců rozptýlených po celém světě.

Jaké jsou trojúhelníky

Obvyklý všestranný trojúhelník je uzavřená geometrická postava složená ze tří segmentů různých délek a tří úhlů, z nichž žádný není správný. Kromě toho existuje několik speciálních typů.

Akutní trojúhelník má všechny úhly menší než 90 stupňů. Jinými slovy - všechny úhly takového trojúhelníku jsou ostré.

Pravý trojúhelník přes které žáci vždycky plakali kvůli hojnosti věty, má jeden úhel o velikosti 90 stupňů nebo, jak se také nazývá, přímkou.

Tupý trojúhelník se vyznačuje skutečností, že jeden z jeho rohů je tupý, to znamená, že jeho velikost je více než 90 stupňů.

Rovinný trojúhelník má tři strany stejné délky. Taková postava má také všechny úhly.

Konečně, v rovnoměrném trojúhelníku tří stran, jsou dva stejné.

Výrazné vlastnosti

Vlastnosti rovnoramenného trojúhelníku také určují jeho hlavní, hlavní, rozdíl - rovnost obou stran. Tyto strany, které se rovnají sobě, se nazývají stehna (nebo častěji boční strany), ale třetí strana se nazývá "nadace".

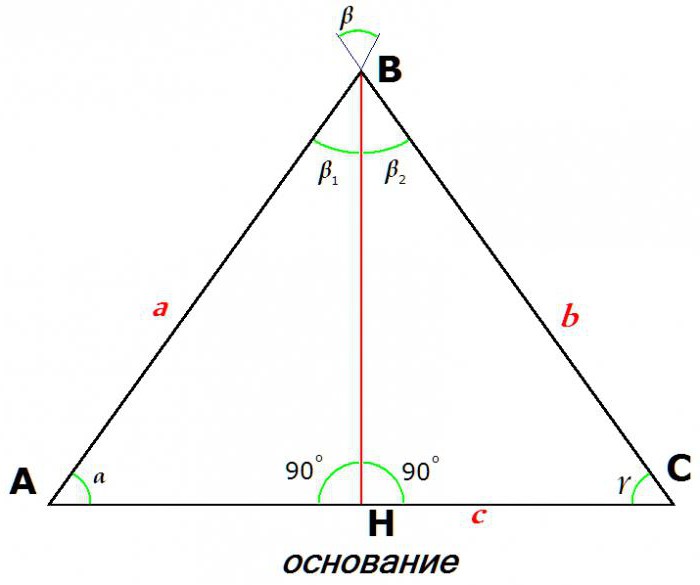
Na tomto obrázku a = b.

Druhý znak rovnoramenného trojúhelníku vyplývá ze sinetické věty. Vzhledem k tomu, že strany a a b jsou stejné, siny jejich protilehlých úhlů jsou stejné:

a / sin γ = b / sin α, odkud máme: sin sin = sin α.

Rovnost sinusů znamená rovnost úhlů: γ = α.

Takže druhým znakem rovnoramenného trojúhelníku je rovnost dvou úhlů sousedících se základnou.

Třetí znamení. Trojúhelník rozlišuje takové prvky, jako je výška, průsečík a medián.

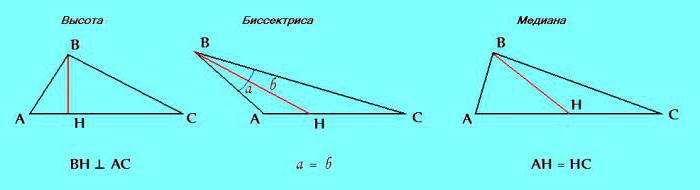
Pokud se v procesu řešení problému ukáže, že v uvažovaném trojúhelníku dva tyto prvky jsou stejné: výška s bisector; bisektor s medián; medián s výškou - lze určitě dospět k závěru, že trojúhelník je rovnoměrný.

Geometrické vlastnosti obrázku

1. Vlastnosti rovnoramenného trojúhelníku. Jednou z charakteristických vlastností čísla je rovnost úhlů sousedících se základnou:

α = γ;

<YOU = <BCA.

2. Další vlastnost diskutovaná výše: medián, průsečík a výška v rovnoměrném trojúhelníku se shodují, pokud jsou postaveny od vrcholu k základně.

3. Rovnost bisektorů odebíraných z vrcholů v základně:

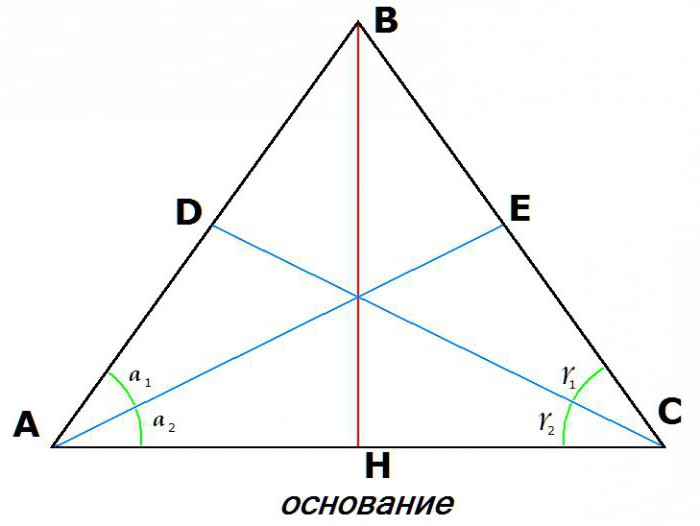
Pokud je AE bisektor úhlu YOU a CD je bisector úhlu BCA, potom: AE = DC.

4. Vlastnosti rovnoramenného trojúhelníku také zajišťují rovnost výšky, která je odvozena od vrcholů v základně.

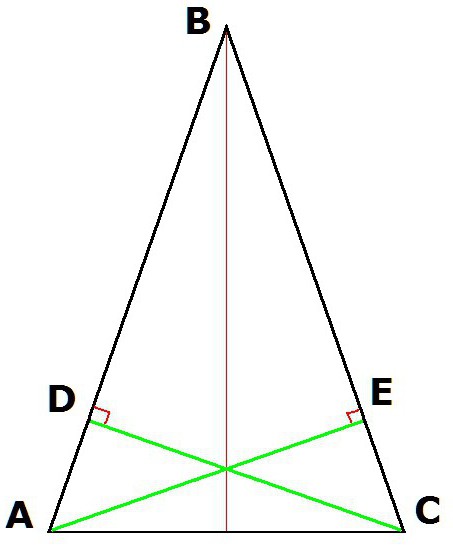
Pokud vytvoříme výšku trojúhelníku ABC (kde AB = BC) od vrcholů A a C, pak výsledné segmenty CD a AE budou stejné.

5. Rovná se také mediánů od zákoutí v základně.

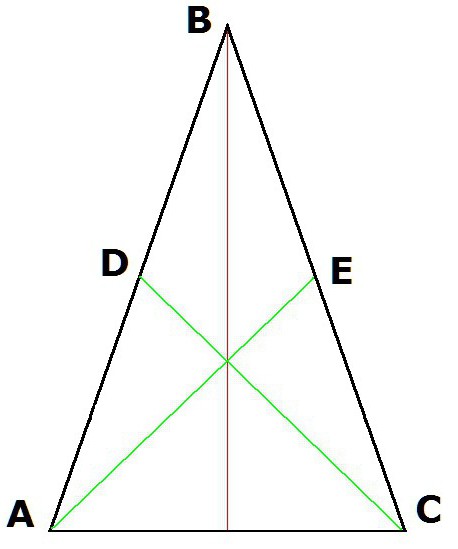
Takže pokud AE a DC jsou mediány, to je AD = DB a BE = EC, pak AE = DC.

Isosceles výška trojúhelníku

Rovnost stran a úhly na nich dodává některé zvláštnosti výpočtu délky prvků uvažovaného čísla.

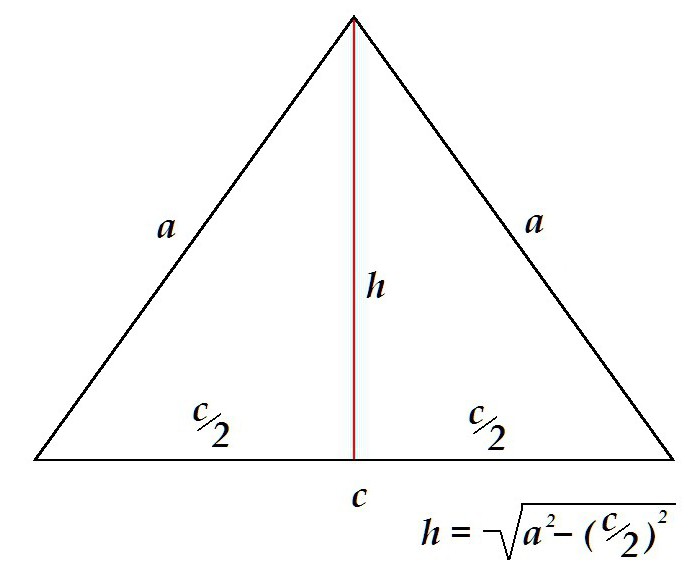
Výška v rovnoměrném trojúhelníku rozděluje obraz na 2 symetrické pravoúhlé trojúhelníky s hypoteny, ve kterých strany vyčnívají. Výška v tomto případě určuje pythagorská věta jako noha.

Trojúhelník může mít všechny tři strany stejné, pak se bude nazývat rovnostranným. Výška v rovnostranném trojúhelníku je určena stejným způsobem, pouze pro výpočty stačí znát pouze jednu hodnotu - délku strany tohoto trojúhelníku.

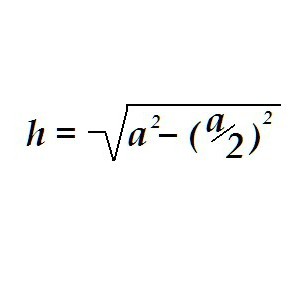
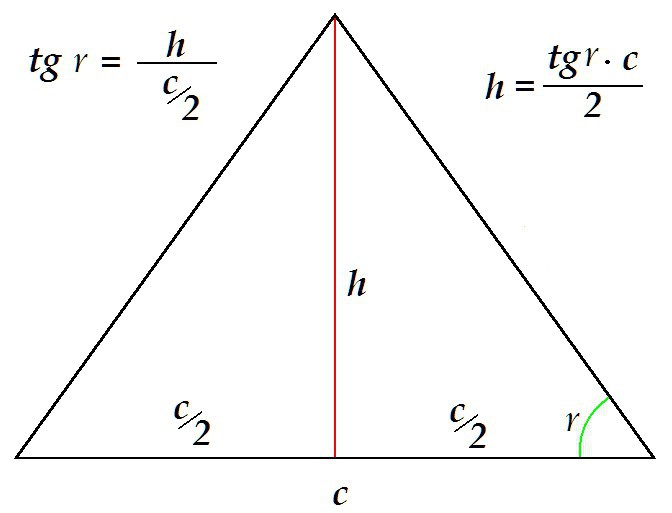
Výšku lze určit jiným způsobem, například znalostí základny a sousedícího úhlu.

Medián rovnoramenného trojúhelníku

Zvažovaný typ trojúhelníku je kvůli jeho geometrickým rysům řešen jednoduše minimálním souborem zdrojových dat. Vzhledem k tomu, že střední hodnota v rovnoměrném trojúhelníku je rovna jak jeho výšce, tak její bisectrix, algoritmus pro její určení se nijak neliší od pořadí, ve kterém jsou tyto prvky vypočítány.

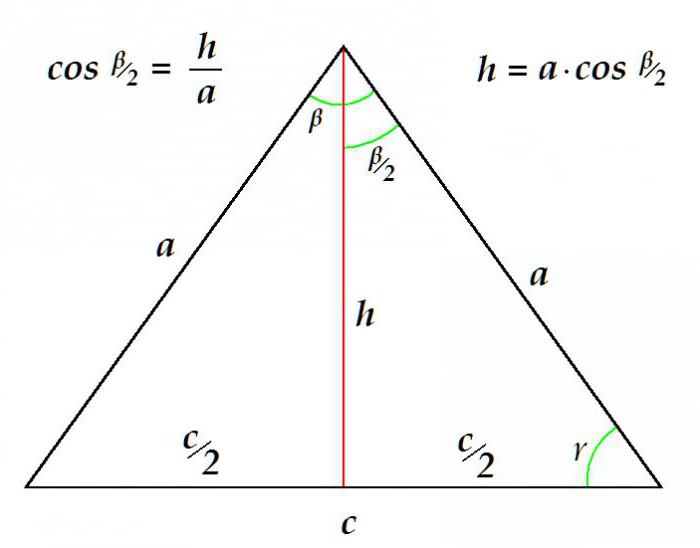
Můžete například určit délku mediánu známou stranou a úhel na vrcholu.

Jak zjistit obvod

Vzhledem k tomu, že u zvažované planimetrické postavy jsou obě strany vždy stejné, pak pro určení obvodu stačí znát délku základny a délku jedné ze stran.

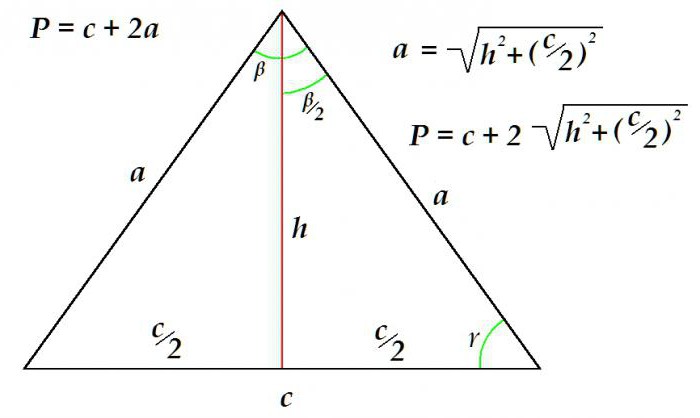
Zvažte příklad, kdy definovat obvod trojúhelníku známou základnou a výškou.

Obvod se rovná součtu základny a dvojnásobku délky strany. Strana, která je po druhé, je určena použitím Pythagorovy věty jako hypotenze pravého trojúhelníku. Jeho délka se rovná druhá odmocnina součtu čtverce výšky a čtverce poloviny základny.

Plocha rovnoramenného trojúhelníku

Existují zpravidla potíže a výpočet plochy rovnoramenného trojúhelníku. Univerzální pravidlo pro určení oblasti trojúhelníku jako poloviny výrobku základny k jeho výšce se samozřejmě používá i v našem případě. Vlastnosti rovnoramenného trojúhelníku však opět usnadňují práci.

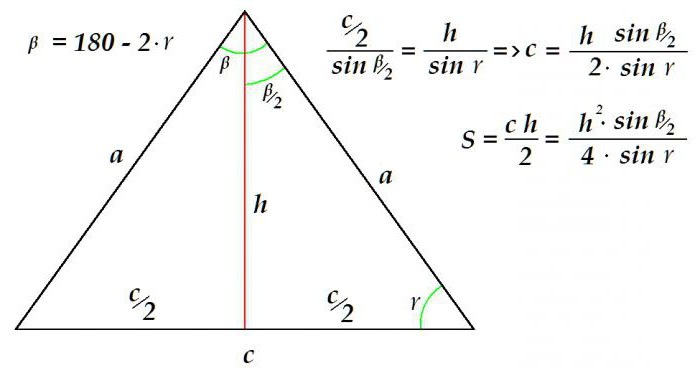
Předpokládejme, že výška a úhel přiléhající k základně jsou známy. Je třeba určit oblast obrázku. Toho lze dosáhnout tímto způsobem.

Vzhledem k tomu, že součet úhlů libovolného trojúhelníku je 180 °, je snadné určit úhel. Dále, za použití poměru vytyčeného podle sinetické věty, je určena délka základny trojúhelníku. Vše, základ a výška - dostatečná data pro určení oblasti - jsou k dispozici.

Další vlastnosti rovnoramenného trojúhelníku

Poloha středu kruhu popsaného kolem rovnoramenného trojúhelníku závisí na úhlu vrcholu. Takže pokud je trojúhelník rovnoměrný, je střed kruhu umístěn uvnitř obrázku.

Střed kruhu, který je popsán kolem tupého rovnoramenného trojúhelníku, leží mimo něj. A konečně, pokud je úhel na vrcholu 90 °, střed leží přesně ve středu základny a průměr kruhu prochází samotnou základnou.

Za účelem určení poloměru kružnice popsané kolem rovnoramenného trojúhelníku stačí rozdělit délku strany dvojitým kosinem o polovinu úhlu na vrcholu.